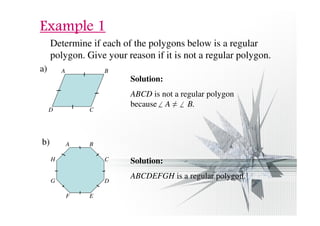
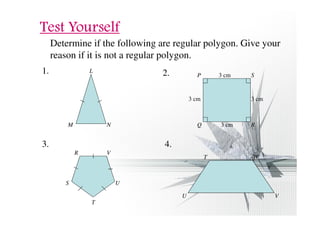
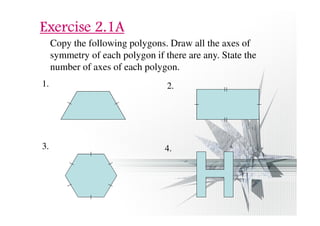
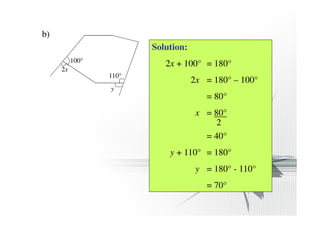
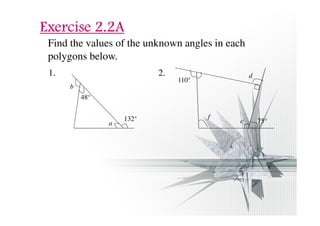
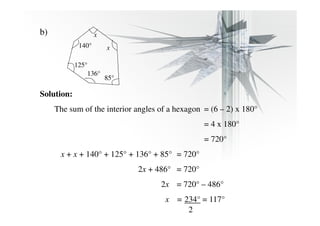
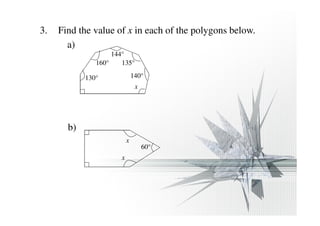
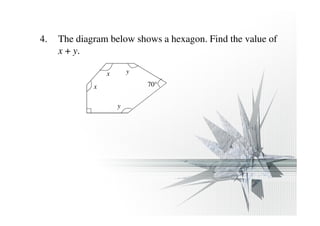
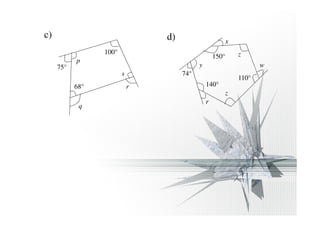
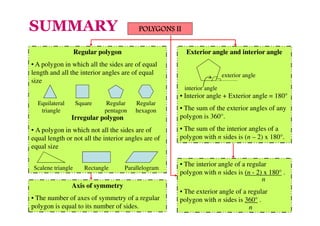
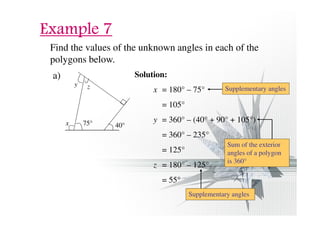
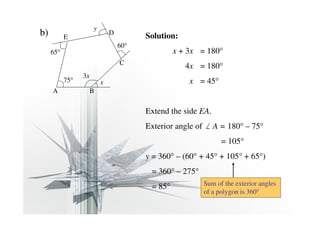
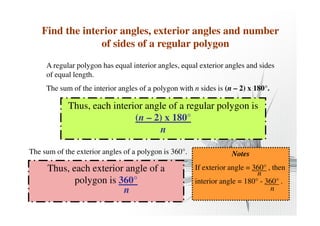
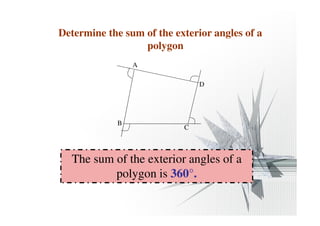
The document discusses properties of regular and irregular polygons, including: - A regular polygon has equal side lengths and interior angles, while an irregular polygon does not. - The interior angle plus exterior angle of any polygon equals 180 degrees. - The sum of the exterior angles of any polygon is 360 degrees. - The sum of the interior angles of an n-sided polygon is (n - 2) × 180 degrees. - For a regular polygon, the interior angle is (n - 2) × 180/n degrees and the exterior angle is 360/n degrees.

1. Mohd Khusaini Majid
Mrsm Kota Kinabalu

2. 2.1 CONCEPT OF REGULAR
POLYGONS
An equilateral triangle has equal
sides and equal interior angles.
Thus, AB = BC = CA and
A = B = C = 60°
A
C B
A
D C
A
B
E
D C
B
A square has equal sides and
equal interior angles. Thus,
AB = BC = CD = DA and
A = B = C = D = 90°
Is all sides of pentagon ABCDE
has the same length and the angles
are of the same size?
RECALL
• The sum of the interior
angles of a triangle is
180°.
• The sum of the interior
angles of a square is
360°.
A regular polygon is a
polygon in which
a) all sides are of equal
length and
b) all interior angles are
of equal size.

3. EEEExxxxaaaammmmpppplllleeee 1111
Determine if each of the polygons below is a regular
polygon. Give your reason if it is not a regular polygon.
a) A
D C
B
Solution:
ABCD is not a regular polygon
because A B.
b) A B
H
G
F
C
D
E
Solution:
ABCDEFGH is a regular polygon.

4. TTTTeeeesssstttt YYYYoooouuuurrrrsssseeeellllffff
Determine if the following are regular polygon. Give your
reason if it is not a regular polygon.
1. L
M N
2. P S
3. 4.
3 cm
3 cm 3 cm
3 cm
Q R
U
T
S
R V
W
T
U V

5. EEEExxxxeeeerrrrcccciiiisssseeee 2222....1111AAAA
Copy the following polygons. Draw all the axes of
symmetry of each polygon if there are any. State the
number of axes of each polygon.
1.
2.
3. 4.

6. 2.2 EXTERIOR AND INTERIOR
ANGLES OF POLYGONS
Find the size of interior and exterior angles
exterior angle
interior angle
In a polygon, the interior and exterior angles lie on a straight line.
Interior angle + Exterior angle = 180°

7. EEEExxxxaaaammmmpppplllleeee 4444
Find the values of x and y in the following polygons.
a)
x
105°
2y y
Solution:
x + 105° = 180°
x = 180° – 105°
= 75°
2y + y = 180°
3y = 180°
y = 180°
3
= 60°

8. b)
100°
2x
110°
y
Solution:
2x + 100° = 180°
2x = 180° – 100°
= 80°
x = 80°
2
= 40°
y + 110° = 180°
y = 180° - 110°
= 70°

9. EEEExxxxeeeerrrrcccciiiisssseeee 2222....2222AAAA
Find the values of the unknown angles in each
polygons below.
1.
b
48°
a
132°
2.
110°
d
c 75°
f

10. Determine the sum of the interior angles of a polygon
RECALL
• The sum of the interior angles of a triangle is 180°.
• The sum of the interior angles of a square is 360°.
What is the sum of the interior angles
of a pentagon, hexagon and other
polygons?
The sum of the interior angles of a polygon
with n sides is (n – 2) x 180°

11. EEEExxxxaaaammmmpppplllleeee 5555
Find the value of x in each of the polygons below.
a)
95°
110° 120°
x
Solution:
Use (n – 2) x 180°
The sum of the interior angles of a pentagon = (5 – 2) x 180°
= 3 x 180°
= 540°
x + 90° + 120° + 95° + 110° = 540°
x + 415° = 540°
x = 540° – 415° = 125°

12. b)
140°
x
x
85°
125°
136°
Solution:
The sum of the interior angles of a hexagon = (6 – 2) x 180°
= 4 x 180°
= 720°
x + x + 140° + 125° + 136° + 85° = 720°
2x + 486° = 720°
2x = 720° – 486°
x = 234° = 117°
2

13. EEEExxxxaaaammmmpppplllleeee 6666
Find the number of sides of a polygon if the sum of its
interior angles is
(a) 1440° (b) 1080°
(a) Let n be the number of sides
of a polygon.
(n – 2) x 180° = 1440°
n – 2 = 1440°
= 8
n = 10
(b) Let n be the number of sides
of the polygon
(n – 2) x 180° = 1080°
n – 2 = 1080°
= 6
n = 8
Solution:
180° 180°

14. EEEExxxxeeeerrrrcccciiiisssseeee 2222....2222BBBB
1. Find the sum of the interior angles of each of the
following polygons.
a) Pentagon
b) Heptagon
c) Decagon
2. Find the number of sides of a polygon if the sum of its
interior angles is
a) 720°
b) 900°
c) 1260°

15. 3. Find the value of x in each of the polygons below.
a)
130°
135°
140°
x
144°
160°
b)
60°
x
x

16. 4. The diagram below shows a hexagon. Find the value of
x + y.
70°
x y
y
x

17. Determine the sum of the exterior angles of a
polygon
B
A
The sum of the exterior angles of a
polygon is 360°.
D
C

18. EEEExxxxaaaammmmpppplllleeee 7777
Find the values of the unknown angles in each of the
polygons below.
a)
40°
y z
x 75°
Solution:
x = 180° – 75°
= 105°
y = 360° – (40° + 90° + 105°)
= 360° – 235°
= 125°
z = 180° – 125°
= 55°
Supplementary angles
Sum of the exterior
angles of a polygon
is 360°
Supplementary angles

19. b)
75°
y
x
3x
65°
60°
E
D
C
A B
Solution:
x + 3x = 180°
4x = 180°
x = 45°
Extend the side EA.
Exterior angle of A = 180° – 75°
= 105°
y = 360° – (60° + 45° + 105° + 65°)
= 360° – 275°
= 85° Sum of the exterior angles
of a polygon is 360°

20. EEEExxxxeeeerrrrcccciiiisssseeee 2222....2222CCCC
1. Calculate the unknown angles in the following
polygons.
a) b)
112°
60°
45°
75°
80°
150°
x
x
x

21. c) d)
110°
75° y
74°
150°
140°
100°
68°
x
z
w
z
r
s
r
p
q

22. Find the interior angles, exterior angles and number
of sides of a regular polygon
A regular polygon has equal interior angles, equal exterior angles and sides
of equal length.
The sum of the interior angles of a polygon with n sides is (n – 2) x 180°.
Thus, each interior angle of a regular polygon is
(n – 2) x 180°
n
The sum of the exterior angles of a polygon is 360°.
Thus, each exterior angle of a
polygon is 360°
n
Notes
If exterior angle = 360° , then
n
interior angle = 180° - 360° .
n

23. EEEExxxxaaaammmmpppplllleeee 8888
Find the size of the interior angle and the exterior angle of
a regular heptagon.
Solution:
A regular heptagon has 7 sides.
Sum of the interior angles = (7 – 2) x 180°
= 900°
Each interior angle = 900°
7
= 128 4°
7
Each exterior angle = 360°
= 51 3°
7
7
ANOTHER WAY: Exterior angle = 180° – Interior angle
= 180° – 128 4° = 51 3°
7 7

24. EEEExxxxaaaammmmpppplllleeee 9999
Find the number of sides of a regular polygon given that
(a) the exterior angle is 72° (b) the interior angle is 140°
Solution:
(a) Let n be the number of sides of the polygon.
360° = 72°
Thus, n = 360
= 5
n
72

25. (b) Let n be the number of sides of the polygon.
(n – 2) x 180° = 140
180n – 360 = 140n
180n - 140n = 360
40n = 360
Thus, n = 360
= 9
n
Another Way: Interior angle = 140°
Exterior angle = 180° - 140°
= 40°
Hence, 360° = 40°
n = 9
n
40

26. EEEExxxxeeeerrrrcccciiiisssseeee 2222....2222DDDD
1. Find the size of the interior and exterior angles of the
following regular polygons.
a) Pentagon
b) Octagon
c) Hexagon
d) Decagon
2. Find the number of sides of a regular polygon, given
that its
a) interior angle is 135°
b) interior angle is 108°
c) exterior angle is 36°
d) exterior angle is 120°

27. Solve problems involving angles and sides of
polygons
EEEExxxxaaaammmmpppplllleeee 11110000
Amin is given a square tile and two regular hexagonal
tiles. All the tiles have sides of equal length.
Determine if he can form a tessellation with these
tiles. If Amin must use the square tile, find two other
tiles which can tessellate with the square tile.

28. Solution:
Understand the problem
Given : One square and two hexagons with sides of
the same length
Find : Sum of one interior angle of a square and one
interior angle of each hexagon
Devising a strategy
Find the interior angles of the three polygons.
Add to see if the sum of the three interior angles
mentioned above 360°.
Stage 1
Stage 2

29. Carrying out the strategy
Interior angle of a square is 90°.
Interior angle of a hexagon is 180° - 360° = 120°
6
Sum of interior angles of the square and two hexagons
is 90° + (2 x 120°) = 330°. Thus, the three tiles do not
tessellate.
If Amin has to use the square tile and needs to find two
tiles which can tessellate with it, each interior angle of
the other two tiles is 360° - 90° = 135°.
2
Stage 3
The sum of the interior angles of the square tile and the two other tiles must be 360°.
Thus, 90° + (2 x interior angle) = 360°
Interior angle = 360° - 90°
2

30. (n – 2) x 180° = 135°
n
180n – 360 = 135n
45n = 360
n = 360 = 8
45
Thus, the other two tiles should be in the shape of an
octagon.
Checking the answer
Use the strategy of working backwards.
If two octagonal tiles are used, each interior angle is
135°.
Sum of the two interior angles of the two tiles is
2 x 135° = 270°.
To tessellate, the interior angle of the third polygon is
360° - 270° = 90°. Thus, a square tile is needed to
tessellate with two octagonal tiles.
Stage 4

31. EEEExxxxeeeerrrrcccciiiisssseeee 2222....2222EEEE
1. In the diagram, ABCD is part of a regular decagon.
FBCG is part of a regular polygon. Calculate
a) the number of sides
b) the sum of the interior angles
of the regular polygon FBCG.
F G
D
B C
A
4°

32. SUMMARY PPPPOOOOLLLLYYYYGGGGOOOONNNNSSSS IIIIIIII
Regular polygon
• A polygon in which all the sides are of equal
length and all the interior angles are of equal
size
Square Regular
pentagon
Irregular polygon
Equilateral
triangle
Regular
hexagon
• A polygon in which not all the sides are of
equal length or not all the interior angles are of
equal size
Scalene triangle Rectangle Parallelogram
Exterior angle and interior angle
interior angle
exterior angle
• Interior angle + Exterior angle = 180°
• The sum of the exterior angles of any
polygon is 360°.
• The sum of the interior angles of a
polygon with n sides is (n – 2) x 180°.
• The interior angle of a regular
polygon with n sides is (n - 2) x 180° .
n
• The exterior angle of a regular
polygon with n sides is 360° .
n
Axis of symmetry
• The number of axes of symmetry of a regular
polygon is equal to its number of sides.