Areas related to circles - Areas of combinations of plane figures for class 10 students.

Areas Related To Circles
Problems based on
Areas of combinations of plane figures
Chapter : Areas Related To Circles Website: www.letstute.com

Problems based on
Q) Find the area of the shaded region, if PQ = 12 cm, PR = 5 cm
and O is the center of the circle.
Given: PQ = 12 cm
PR = 5 cm
To find: Area of the shaded region = ?
O
5 cm
12 cm
Q
R P

Problems based on
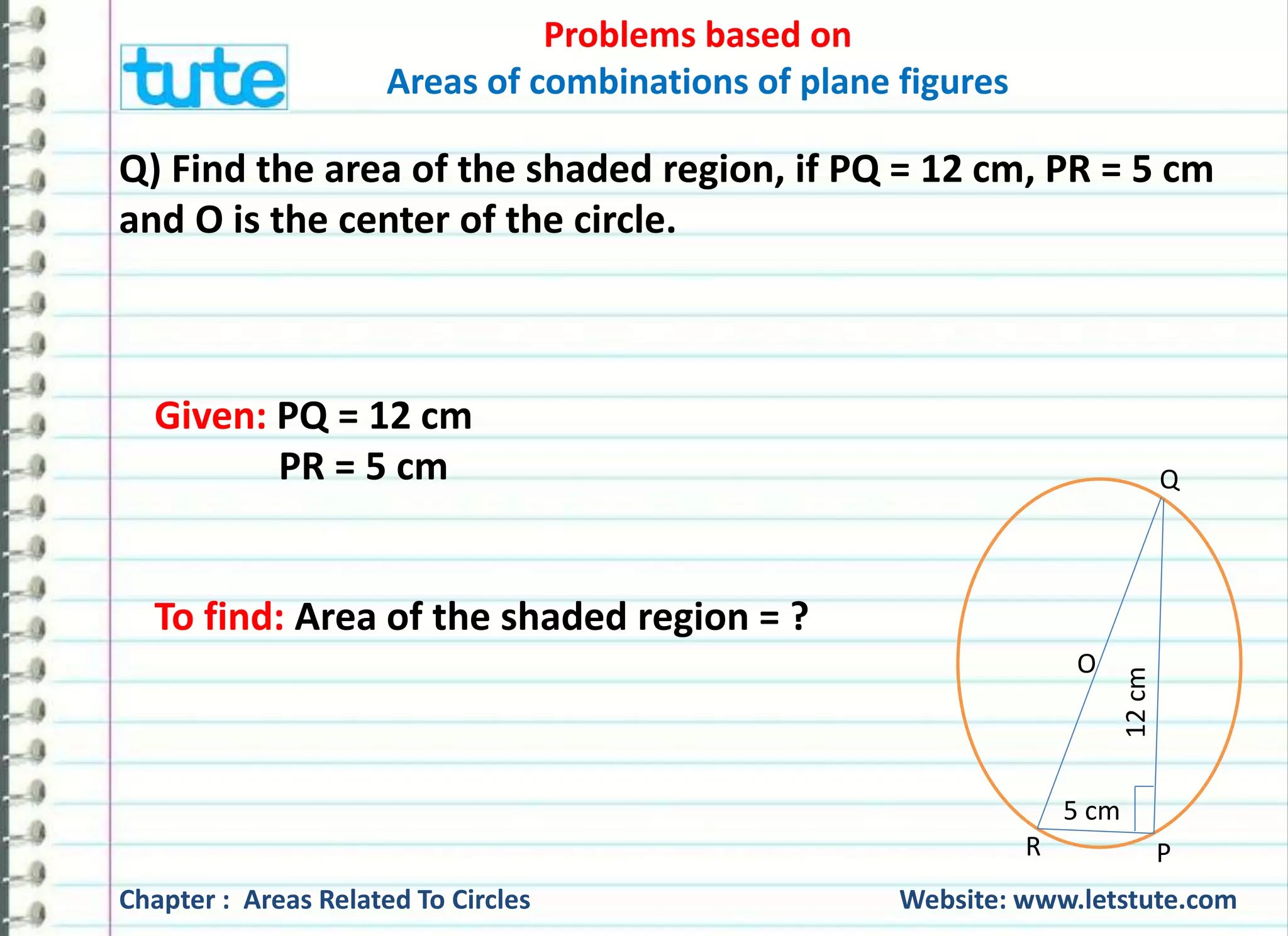
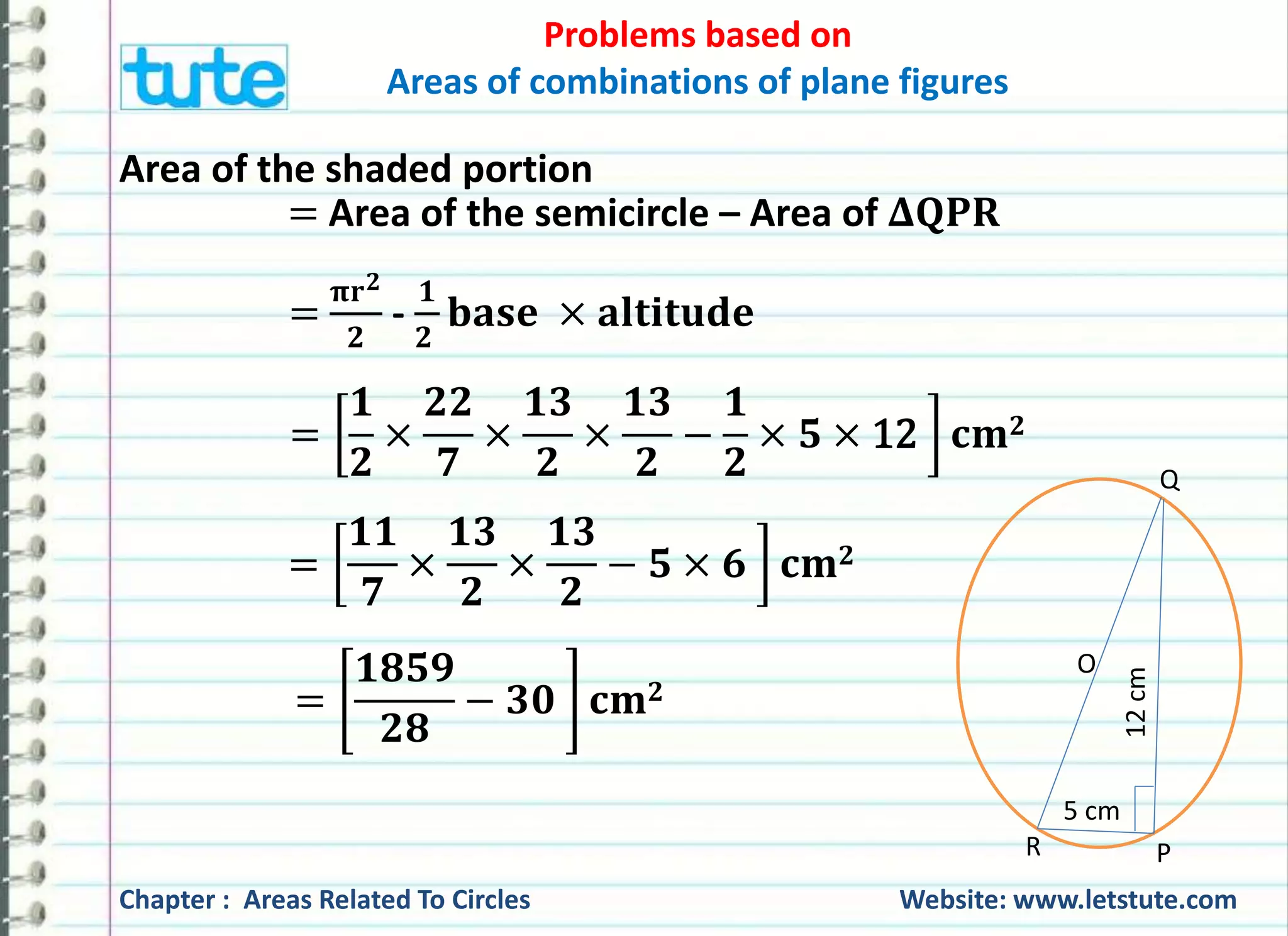
Solution: QR is the diameter.
∴ ∠ 퐐퐏퐑 = ퟗퟎퟎ [Angle in a semicircle]
In right triangle QPR, we have,
QR2 = PR2 + QP2 [By pythagoras’ theorem]
QR2 = (5 cm)2 + (12 cm)2
QR2 = 25 cm2 + 144 cm2
Q
O
5 cm
12 cm
R P
QR2 = 169 cm2

Problems based on
QR = ퟏퟔퟗ퐜퐦ퟐ
QR = 13 cm
Radius OR = OQ =
퐐퐑
ퟐ
=
ퟏퟑ
ퟐ
cm
Q
O
5 cm
12 cm
R P

Problems based on
Area of the shaded portion
=Area of the semicircle – Area of 횫퐐퐏퐑
O
5 cm
12 cm
Q
× ퟓ × 12 퐜퐦ퟐ
R P
=
훑퐫ퟐ
ퟐ
-
ퟏ
ퟐ
퐛퐚퐬퐞 × 퐚퐥퐭퐢퐭퐮퐝퐞
=
ퟏ
ퟐ
×
ퟐퟐ
ퟕ
×
ퟏퟑ
ퟐ
×
ퟏퟑ
ퟐ
−
ퟏ
ퟐ
=
ퟏퟏ
ퟕ
×
ퟏퟑ
ퟐ
×
ퟏퟑ
ퟐ
− ퟓ × ퟔ 퐜퐦ퟐ
=
ퟏퟖퟓퟗ
ퟐퟖ
− ퟑퟎ 퐜퐦ퟐ

Problems based on
ퟏퟖퟓퟗ − ퟖퟒퟎ
ퟐퟖ
퐜퐦ퟐ
ퟏퟎퟏퟗ
ퟐퟖ
퐜퐦ퟐ
Q ퟑퟔ. ퟑퟗퟑ cm2
O
5 cm
12 cm
R P
=
=
=
Hence, the area of the shaded region
is 36.393 cm2

Problems based on
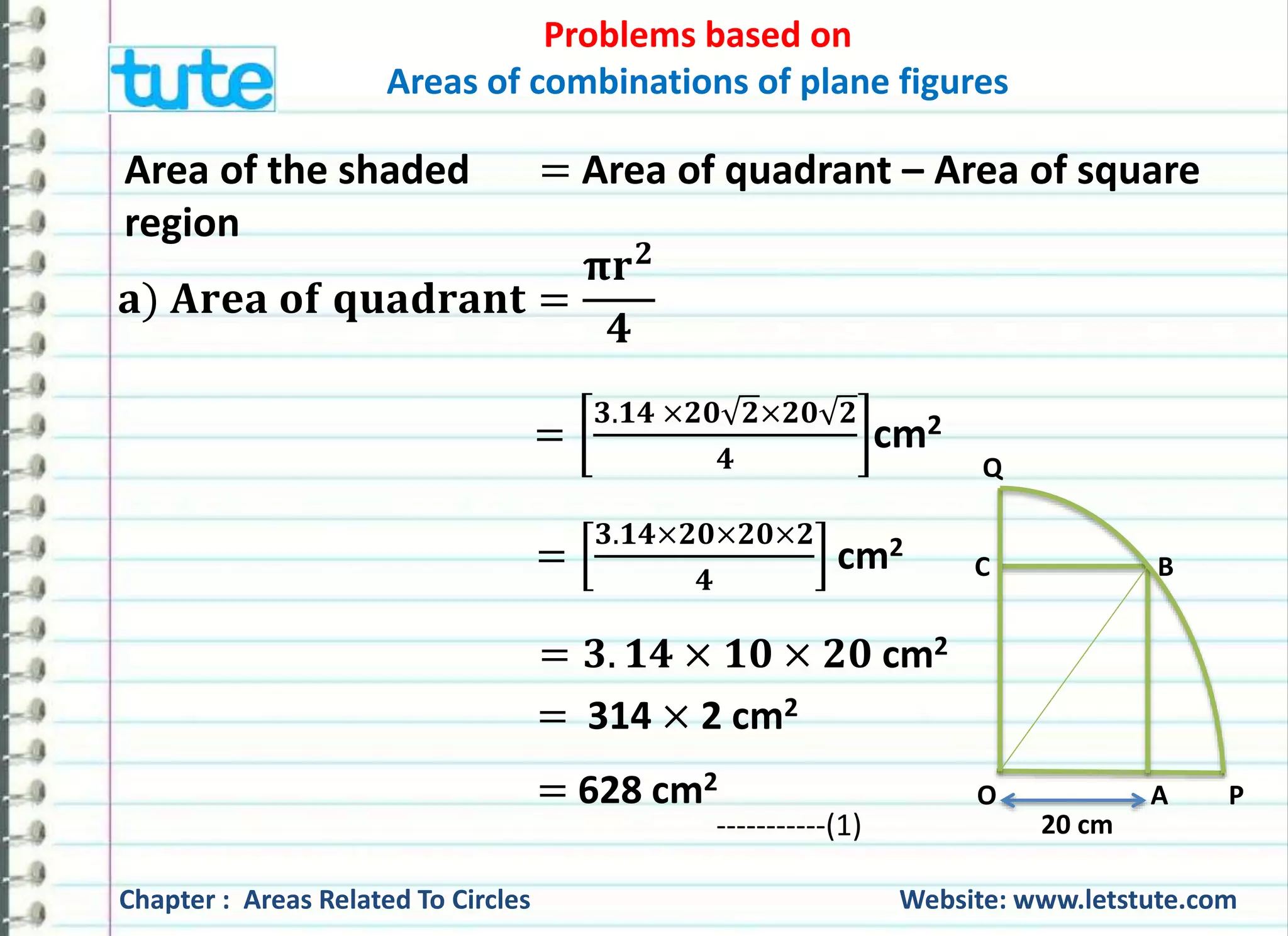
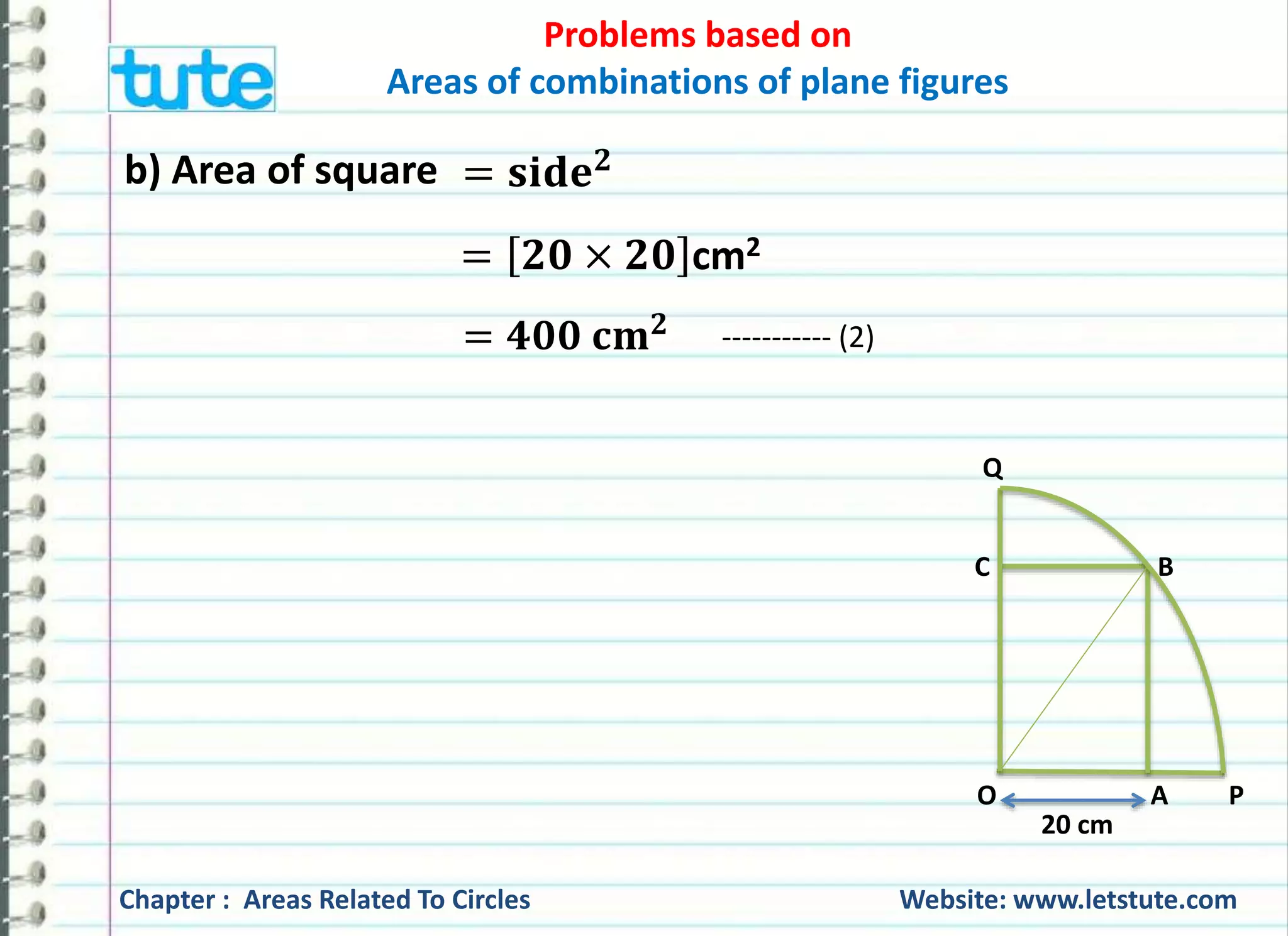
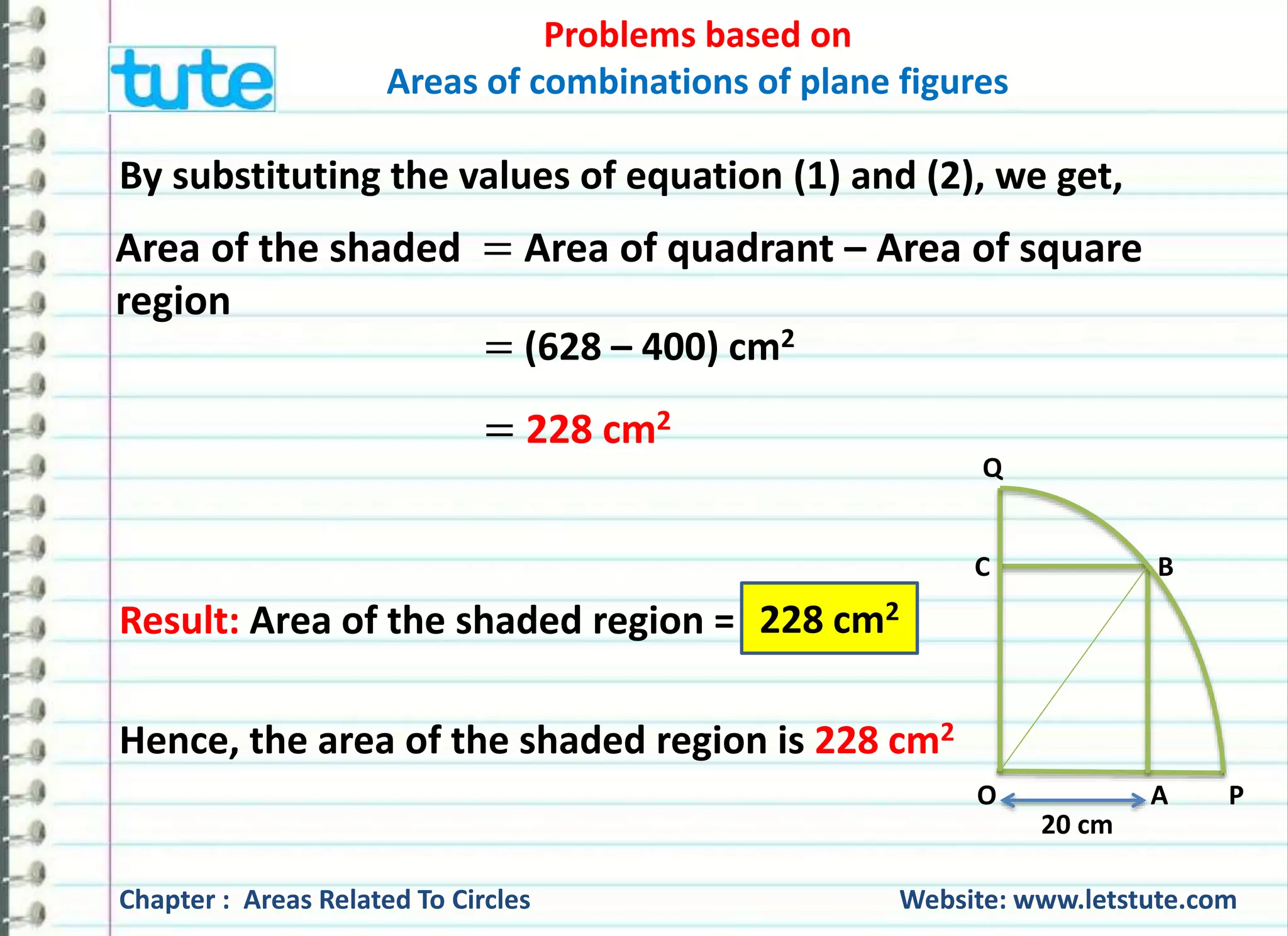
Q) A square OABC is inscribed in a quadrant OPBQ. If OA = 20
cm, find the area of the shaded region. [Use 흅 = ퟑ. ퟏퟒ]
Given: OA = 20 cm
To find: Area of the shaded region = ?
Q
C B
O A P
20 cm

Problems based on
Solution: Join OB
By Pythagoras theorem, we get,
OB2 = OA2 + AB2
= (202 + 202)cm
= (400 + 400) cm
= 800 cm
= 20 ퟐ cm
Let ‘r’ be the radius of the quadrant.
Then, r = OB = 20 ퟐ 퐜퐦
Q
C B
O A P
20 cm

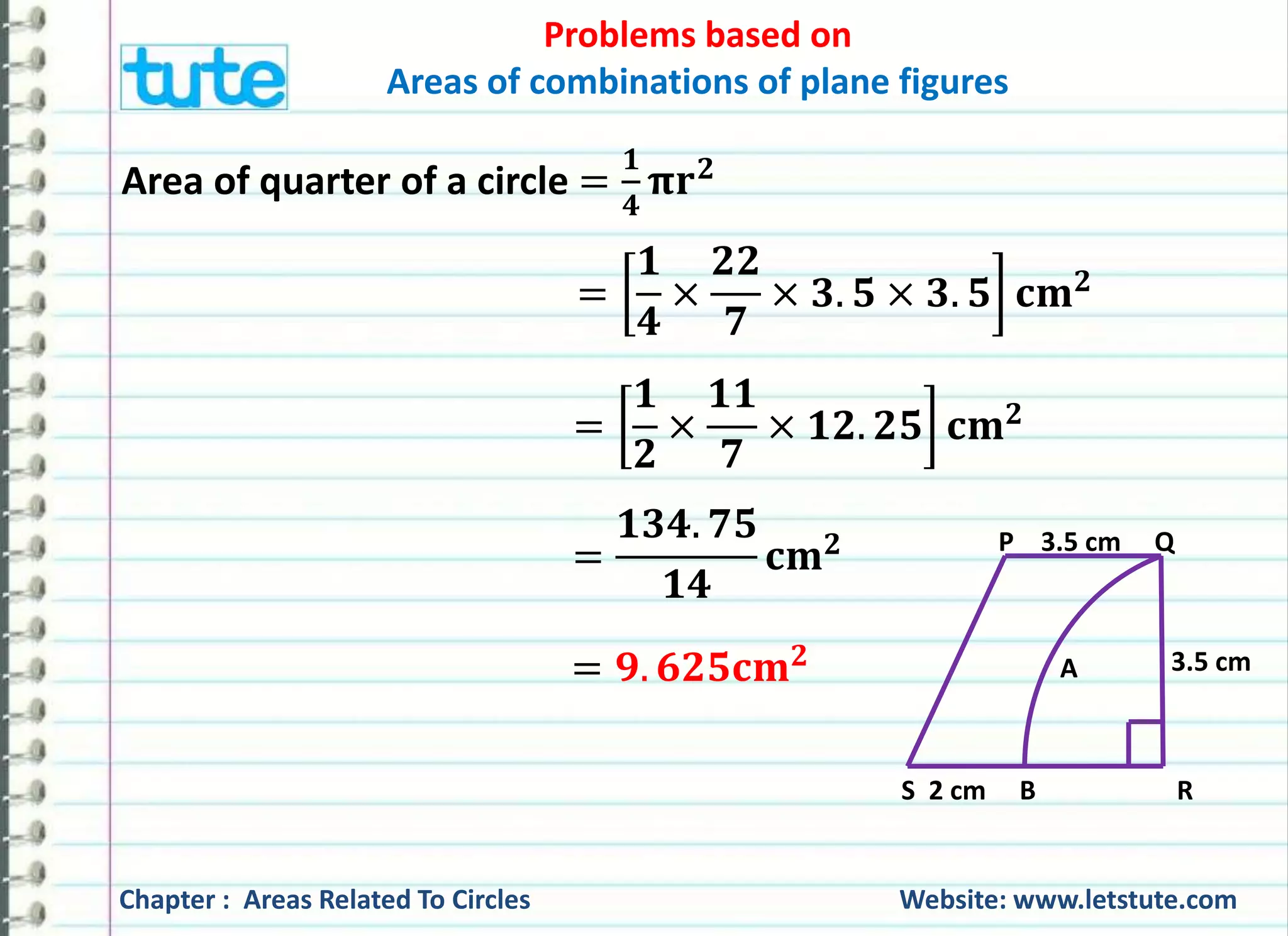
Problems based on
Area of the shaded = Area of quadrant – Area of square
region
퐚) 퐀퐫퐞퐚 퐨퐟 퐪퐮퐚퐝퐫퐚퐧퐭 =
훑퐫ퟐ
ퟒ
=
ퟑ.ퟏퟒ ×ퟐퟎ ퟐ×ퟐퟎ ퟐ
ퟒ
cm2
Q
ퟑ. ퟏퟒ × ퟐퟎ × ퟐퟎ × ퟐ
cm2
= C B
O A P
20 cm
ퟒ
= ퟑ. ퟏퟒ × ퟏퟎ × ퟐퟎ cm2
= 314 × 2cm2
= 628 cm2
-----------(1)

Problems based on
b) Area of square = 퐬퐢퐝퐞ퟐ
= ퟐퟎ × ퟐퟎ cm2
Q
C B
O A P
20 cm
= ퟒퟎퟎ 퐜퐦ퟐ ----------- (2)

Problems based on
By substituting the values of equation (1) and (2), we get,
Area of the shaded = Area of quadrant – Area of square
region
= (628 – 400) cm2
=228 cm2
Q
C B
O A P
20 cm
Result: Area of the shaded region = 228 cm2
Hence, the area of the shaded region is 228 cm2

Problems based on
Q) From a piece of cardboard, in the shape of trapezium PQRS,
PQ ∥ SR and ∠퐐퐑퐒 = ퟗퟎퟎ, 퐪퐮퐚퐫퐭퐞퐫 퐜퐢퐫퐜퐥퐞 퐐퐀퐁퐑 퐢퐬 퐫퐞퐦퐨퐯퐞퐝.
Given SB = 2 cm, PQ = QR = 3.5 cm, calculate the area of the
remaining piece of the cardboard.
Given: PQ ∥SR
∠퐐퐑퐒 = ퟗퟎퟎ
퐒퐁 = ퟐ퐜퐦,
퐏퐐 = 퐐퐑 = ퟑ. ퟓ 퐜퐦
To find: The area of the remaining piece of
the cardboard = ?
P 3.5 cm Q
A
3.5 cm
S 2 cm B R

Problems based on
Solution: PQ = 3.5 cm,
SR = SB + BR = SB + QR = (2+3.5) cm = 5.5 cm ---------------- (1)
[∵ BR = QR = 3.5 cm, radii of the circle]
Area of trapezium PQRS =
ퟏ
ퟐ
× 퐬퐮퐦 퐨퐟 퐩퐚퐫퐚퐥퐥퐞퐥 퐥퐢퐧퐞퐬 × 퐡퐞퐢퐠퐡퐭
P 3.5 cm Q
3.5 cm
A
퐏퐐 + 퐒퐑 × 퐐퐑
S 2 cm B R
=
ퟏ
ퟐ

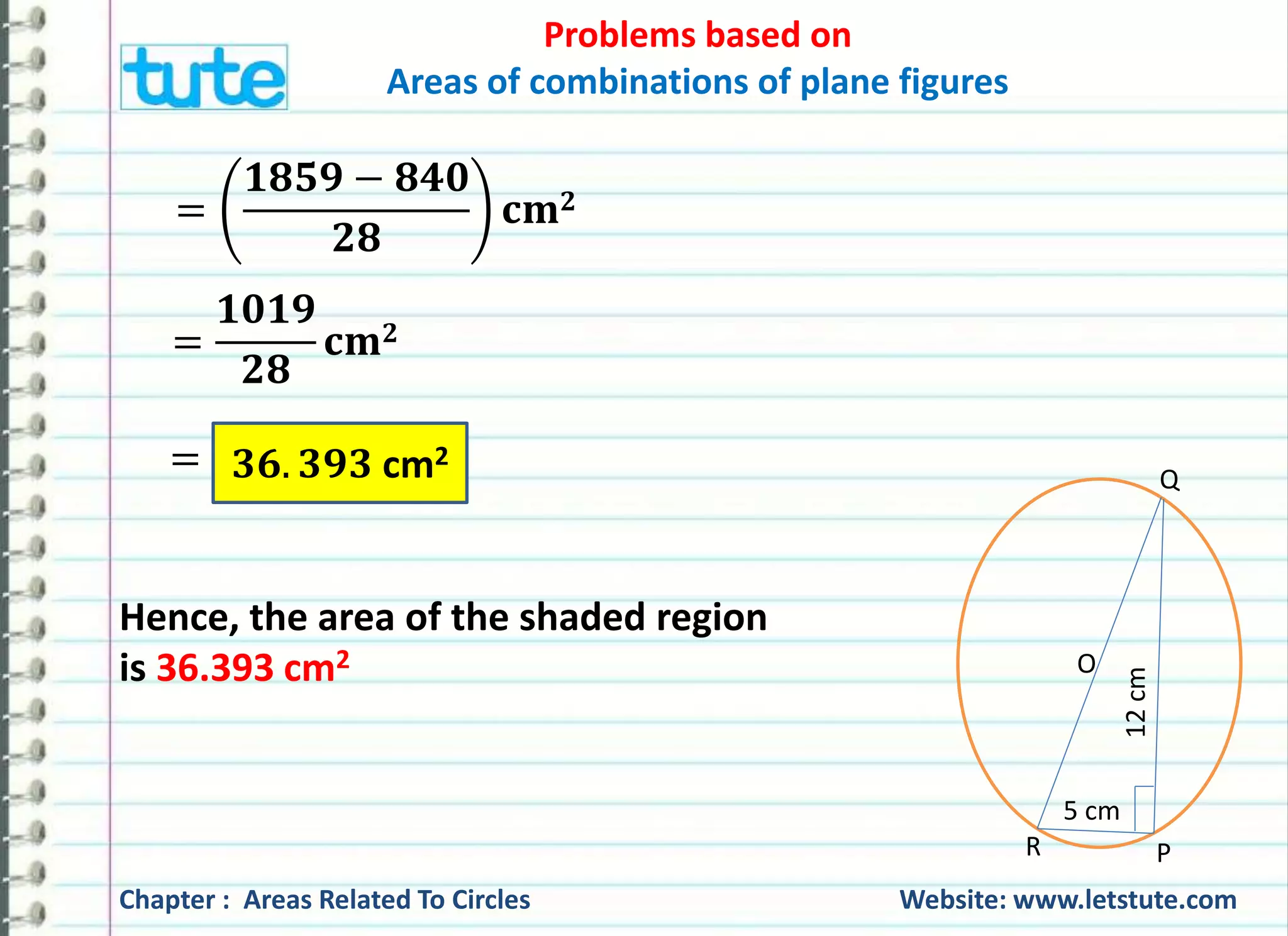
Problems based on
=
ퟏ
ퟐ
(ퟑ. ퟓ + ퟓ. ퟓ) × ퟑ. ퟓ퐜퐦ퟐ
=
ퟏ
ퟐ
× ퟗ × ퟑ. ퟓ퐜퐦ퟐ
[Using (1)]
=
ퟗ × ퟑ. ퟓ
ퟐ
퐜퐦ퟐ
=
ퟑퟏ. ퟓ
ퟐ
퐜퐦ퟐ
= ퟏퟓ. ퟕퟓ 퐜퐦ퟐ
P 3.5 cm Q
3.5 cm
A
S 2 cm B R

Problems based on
Area of quarter of a circle =
ퟏ
ퟒ
훑퐫ퟐ
=
ퟏ
ퟒ
×
ퟐퟐ
ퟕ
× ퟑ. ퟓ × ퟑ. ퟓ 퐜퐦ퟐ
=
ퟏ
ퟐ
×
ퟏퟏ
ퟕ
× ퟏퟐ. ퟐퟓ 퐜퐦ퟐ
=
ퟏퟑퟒ. ퟕퟓ
ퟏퟒ
퐜퐦ퟐ
= ퟗ. ퟔퟐퟓ퐜퐦ퟐ
P 3.5 cm Q
A
3.5 cm
S 2 cm B R

Problems based on
Area of the remaining part
= (Area of trapezium PQRS – Area of quarter of a circle)
= (15.75 – 9.625) 퐜퐦ퟐ
=
6.125 퐜퐦ퟐ
Hence, the area of the remaining piece of
the cardboard is 6.125 퐜퐦ퟐ
P 3.5 cm Q
A
3.5 cm
S 2 cm B R

Problems based on
Q) Four goats are tethered at four corners of a square plot of side
56 m so that they just cannot reach one another. Calculate the
area that remains ungrazed.
Given: Side of a square plot = 56 m
To find: Ungrazed area = ?

Problems based on
Solution: The four goats tethered at the four corners of the
square plot will be able to graze four quadrants, each of radius r
(say).
퐃퐢퐚퐦퐞퐭퐞퐫
Then, r =
ퟐ
=
ퟓퟔ
ퟐ
퐦
= 28 m

Problems based on
Ungrazed area = 퐀퐫퐞퐚 퐨퐟 퐭퐡퐞 퐬퐪퐮퐚퐫퐞 − 퐀퐫퐞퐚 퐨퐟 ퟒ 퐪퐮퐚퐝퐫퐚퐧퐭퐬
a) Area of the square = (퐬퐢퐝퐞)ퟐ
= ퟓퟔ ퟐ 퐦ퟐ
= ퟑퟏퟑퟔ 퐦ퟐ ----------(1)

Problems based on
퐛) 퐀퐫퐞퐚 퐨퐟 ퟒ 퐪퐮퐚퐝퐫퐚퐧퐭퐬 = ퟒ ×
훑퐫ퟐ
ퟒ
= ퟒ ×
ퟐퟐ
ퟕ
×
ퟐퟖ × ퟐퟖ
ퟒ
퐦ퟐ
= ퟐퟐ × ퟒ × ퟐퟖ 퐦ퟐ
= ퟖퟖ × ퟐퟖ 퐦ퟐ
= ퟐퟒퟔퟒ 퐦ퟐ
------(2)

Problems based on
By substituting the values of equation (1) and (2), we get,
Ungrazed area = 퐀퐫퐞퐚 퐨퐟 퐭퐡퐞 퐬퐪퐮퐚퐫퐞 − 퐀퐫퐞퐚 퐨퐟 ퟒ 퐪퐮퐚퐝퐫퐚퐧퐭퐬
= (ퟑퟏퟑퟔ − ퟐퟒퟔퟒ) 퐦ퟐ
=
672퐦ퟐ
Hence, the ungrazed area is 672 퐦ퟐ

Areas related to circles - Areas of combinations of plane figures for class 10 students.

More Related Content

What's hot

Similar to Areas related to circles - Areas of combinations of plane figures for class 10 students.

More from Let's Tute

Recently uploaded

Areas related to circles - Areas of combinations of plane figures for class 10 students.