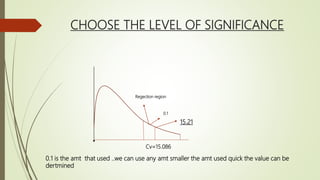
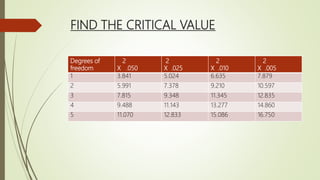
The chi-square test is used to compare observed data to expected data. It determines if differences between the observed and expected numbers are due to chance or something more significant. The chi-square test has several key steps: stating the null and alternative hypotheses, choosing a significance level, finding the critical value, calculating the test statistic by summing the squared differences between observed and expected values divided by the expected value, and making a conclusion by comparing the test statistic to the critical value. The chi-square test has assumptions of adequate sample sizes and independence of data. It is useful for testing goodness of fit, independence of attributes, and homogeneity.

1. CHI SQUARE TEST
1st M.COM (IB)
VIKAS KUMAR

2. DEFINATION AND MEANING
What is chi square test ?
It is a statistical test used to compare expected data
with what we collected
Chi square test is tell us the difference between
collected no and the expected no
If the difference is large then there will be some thing
for the significant change
So it is also called as goodness to fit test

3. Important terms
 PARAMETRIC TEST-
in this test population constant like mean , std.deviation , std.error, co-relation , co-efficient
proportion etc. and data tend to follow one assumed or established such as normal, binominal
etc.
 NON PARAMETRIC TEST –
The test in which the no content of the population is used data do no follow any specific
distribution and no assumption are made in these test e.g. : to classify the goods better and
best we use the arbiter numbers or marks to each category
 HYPOTHESIS -
 DEGREE OF FREEDOM
 CONTINGENCY TABLE

4. EXPLANATION OF CHI SQUARE TEST
# 1 2 3 4 5 6
Possibility's 22 24 38 30 46 44
# 1 2 3 4 5 6
Possibility's 34 34 34 34 34 34
OBSERVED VALUE -
EXPECTED VALUE -
total=204
#=dies value
E(1)=204(1/6)=34 E(2)=204(1/6)=34

5. STEPS FOR PERFORMANCE OF CHI SQUARE
TEST/HYPOTHESIS TEST
State null (Ho) or alternative hypothesis (Ha)
Choose the level of significance (infinite)
Find the critical value
Find the test statistics
Conclusion

6. STATE NULL (HO) OR
ALTERNATIVE HYPOTHESIS (HA)
Null hypothesis
Ho=dies is fair
Observation fit the operation value
Alternative hypothesis
Ha=dies is no fair

7. CHOOSE THE LEVEL OF SIGNIFICANCE
Regection region
0.1
Cv=15.086
0.1 is the amt that used ..we can use any amt smaller the amt used quick the value can be
dertmined
15.21

8. FIND THE CRITICAL VALUE
Degrees of
freedom
2
X .050
2
X .025
2
X .010
2
X .005
1 3.841 5.024 6.635 7.879
2 5.991 7.378 9.210 10.597
3 7.815 9.348 11.345 12.835
4 9.488 11.143 13.277 14.860
5 11.070 12.833 15.086 16.750

9. FIND THE TEST STATISTICS
2 2
X = sum
 (22-34)2/34
 (24-34)2/34……………..till last unit the total will be
15.21 test statistics
(o-e)
e

10. ASSUMPTIONS
 2 KEY ASSUMPTIONS TO BE AWARE OF BEFORE APPLYING THE CHI-
SQUARE TEST
 Sample Size Assumption:
The chi-square test can be used to determine differences in proportions using a two-by-
two contingency table. ...
 Independence Assumption:
Secondly, the chi-square test cannot be used on correlated data.

11. LIMITATIONS OF THE CHI-SQUARE TEST
The chi-square test does not give us much information about the
strength of the relationship or its substantive significance in the
population.
The chi-square test is sensitive to sample size. The size of the
calculated chi-square is directly proportional to the size of the
sample, independent of the strength of the relationship between
the variables
The chi-square test is also sensitive to small expected frequencies
in one or more of the cells in the table.

12. WHAT IS THE USE OF CHI SQUARE
TEST?
The chi-squared test is used to determine whether
there is a significant difference between the expected
frequencies and the observed frequencies in one or
more categories.

13. APPLICATION OF A CHI SQUARE TEST
Good ness of fit of distribution
Test of independence of attributes
Test of homogeneity

14. Conclusion
The chi-square test is no doubt a most
frequently used test, but its correct
application is equally an uphill task.

15. Thank you