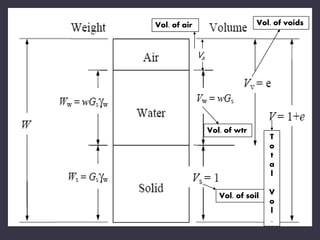
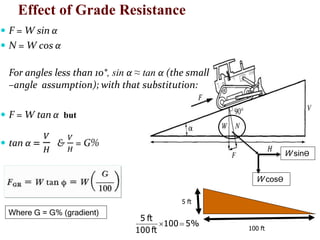
The document discusses selecting equipment for earthmoving projects based on analyzing the mechanical capabilities of machines and the properties of materials to be handled. It emphasizes that the contractor must choose equipment that can economically relocate and process bulk materials. Key factors in the decision process include the task properties of the material, and matching the machine's abilities. The engineer must calculate required power by considering rolling resistance and grade resistance to determine if a machine is suitable.

1. PREPARED BY:-
Mr. Karm P. Balar
Asst. Professor
CED, SURAT

2. The Major Portion of The Work on The Heavy Construction Project Consists of
Handling And Processing The Bulk Material on Site.
The Contractor Must Select The Proper Equipment To Relocate And For Process This
Material Economically.
The Decision Process For Matching The Best Possible Machine To The Project Task,
The Properties of The Material, And To Be Handle With The Mechanical Capabilities
of The Machine is Taken into The Account.
Almost Every Civil Engineering Project Start With Earth Work Whether It May involve
Excavation Work or Filling Work or Both Work.
in Case of Dam, Highway, Airport, Etc. The First Phase of The Construction is Earth
Work And Its Also in Large Magnitude.
INTRODUCTION

3. Soil fundamental
Material property
Soil weight – volume
relationships
Volumetric measure.
SOIL FUNDAMENTALS

4.  in contract document the excavation work is classify as common work, Rock work,
muck work, or unclassified work.
 common work refer to ordinary Earth excavation.
 unclassified reflect the lake of clear distinction between soil and the rock particle.
 the removal of common work will not required the use of explosive.
 in construction, rock is a material which cannot be removed by ordinary Earth
hauling equipment.
 Rock must be removed by drilling and blasting or by some other method which
result in greater expanses than the earth excavation work.

5. S:
W:
A:
Solid
Liquid
Air
Soil particle
Water particle
Air particle
5

6. SOIL WEIGHT – VOLUME Relation SHIP
in a mass of soil, there are three physical components: solid, water, and air. A phase
relationship diagram is normally used to represent the relationship as follows:

7. Vol. of soil
Vol. of wtr
Vol. of air
Va
T
o
t
a
l
V
o
l
.
Vol. of voids

8. SOIL AS A THREE PHASE SYSTEM
8
V = Total volume of soil mass
Vs = Volume of soil solids
Vw = Volume of water
Va = Volume of air
Vv = Va+Vw = Volume ofvoids
W = Total weight of soil
Ws = Weight of soil solids
Wa = Weight of air ≈ 0
Ww = Weight of water

10. (0 < e < ∞)
For sands, 0.5 ≤ e ≤ 0.9
For clays, 0.7 ≤ e ≤ 1.5 (or even higher)
Volume of solids (Vs )
1) Void ratio, e
e 
Volume of voids (Vv )
2. VOLUMETRIC RATIOS
10

11. 2) Porosity, n
(0 < n < 1)
Typical range, 9-70%
For sands, 25% ≤ n ≤ 50%
3) Air Porosity, na’ a(0 < n ’< 1)
4) Percentage Air Voids, na a(0 < n < 1)
Total volume of soil sample (Vt )
Volume of voids (Vv)
n 
VOLUMETRIC RATIOS
t
a
Total volume of soil sample (V )
Volume of air (Va)
n ' 
Volume of voids (Vv)
Volume of air (V )
na  a
11

12. (0 < Sr <100%)
6) Volumetric Water Content, θv
v
(0 < θ < 1)
VOLUMETRIC RATIOS
Total volume of voids (Vv )
5) Degree of Saturation/ Saturation Ratio, S (or Sr)
S 
Volume of voids containing water (Vw )
100%
t
w
v
Total volume of soil sample (V )
Volume of voids containing water (V )
 
12

13. 1) Moisture/Water Content/Gravimetric Water Content, w
(0 < w < ∞)
Typical value for Sands >> 10-30%
For clays >> 10% or higher typically
For some organic soils w>100%, even up to 500%.
For quick clays w is typically > 100%.
3. WEIGHT RELATIONSHIPS
100%
Weight of soil solids (Ws )
Weight of water(Ww )
w 
13

14. 2) Unit Weight, γ
3) Dry Unit Weight, γd
5) Unit Weight of Soil Solids, γs
WEIGHT RELATIONSHIPS
(kN m3
;lb ft3
; g cm3
)
Weight

Mg
Volume V
t
s
d
VTotal Volume
Weight of soil solids W
 
t
b
Total Volume V
4) Bulk Unit Weight, γb
 
Total Weight

W
s
14
s
s
Volume of soil soilds V
Weight of soil soilds W
 

15. 6) Saturated Unit Weight, γsat
7) Submerged Unit Weight, γsub (orγbouyant)
WEIGHT RELATIONSHIPS
wsub sat
γw = 9.81 kN/m3 → 1g/cm3
= 1000 kg/m3
= 62.4 lb/ft3
Total Volume
15
sat

Weight of saturated soil

Archimede’s principle:
The buoyant force on a body immersed
in a fluid is equal to the weight of the
fluid displaced by that object.

16. SPECIFIC GRAVITY (Gs)
w
16
s
Unit weight of soil soilds

s
G 
Unit weight of equal volume of water at 4C 
Generally for soils 2.6 ≤ Gs ≤ 2.7

17.  For bulk materials volumetric measure varies with the material’s position in the
construction process. the same weight of material will occupy a different volume as
the material is handled on the project.
The soil volume is measured in in three different state…
 Bank cum.... 1 cum of material as it lies in the natural state Bcy
 Loose cum... 1 cum of material after it has been disturbed by a loading process Lcy
 Compacted cum.... 1 cubic of material in the compacted state also referred to as a net
in place cum Ccy
 in planning for estimating a job, the engineer must use a consistent volumetric state
in any set of calculations. the necessary of consistency in unit is achieved by the use
of shrinkage and swell factors

18. •Shrinkage factor:
Shrinkage factor (for compacted)
(compacted dry unit weight/bulk dry unit weight)
Shrinkage %
{(compacted unit wt.) – (bank unit wt.)/ compacted unit wt.)} x
Swell factor (for Dry)
Swell factor=(loose dry unit weight/bulk dry unit weight)
Swell % =(Bank unit weight/loose unit weight - 1) x 100

19. Equipment Power Requirements
 The contractor must select the proper equipment to relocate
and/or process materialseconomically.
 The analysis procedure for matching the best possible machine to
the project task requires inquiry into a machine’s mechanical
capability.
 The engineer must first calculate the power required to propel the
machine and itsload.
 This powerrequirement is established by two factors:
1. Rolling Resistance
2. Grade Resistance
 Equipment manufacturers publish performance charts for individual
machine models.
 These charts enable the equipment planner to analyze a machine’s
ability to perform under a given set of job and load conditions.

21. Rolling Resistance
The resistance of a level surface to constant-velocity motion across it.
To determine the maximum speed of a vehicle in a specific situation, it is necessary
to determine the total resistance to movement of the vehicle.
Total resistance = Grade resistance + Rolling resistance
 Resistance may be expressed in kilograms per metric ton,
Rolling resistance is primarily due to
tire flexing
penetration of the travel surface.,

22. Rolling Resistance
 The rolling resistance in pounds pergross ton is . . .
R =
𝑃
𝑊
Where:
R = Rolling resistance in pounds OR KG/ Tone
P = Total tension in tow cable inKG
W = Gross weight of truck in tons

23. Rolling Resistance

24. Rolling Resistance
When tire penetration is known, an approximate rolling
resistance value for a wheeled vehicle can be calculated . . .
RR = [40 + (30 * TP)] * GVW
Where:
RR = Rolling resistance in pounds
TP = Tire penetration in inches
GVW = Gross vehicle weight intons

26. The force-opposing movement of a machine up a frictionless slope.
Grade resistance factor (kg/t) = 10  grade (%)
Grade resistance (kg) may be calculated = Vehicle weight (t)  Grade
resistance factor (kg/t)
Grade Resistance

27.  Effective Grade
 Effective grade may be easily calculated by use of Equation
Rolling resistance factor (kg/t)
Effective grade (%) =Grade (%)
10


29. 5 ft
100 ft
5%100
ft100
ft5

Effect of Grade Resistance
Where G = G% (gradient)
W cosӨ
W sinӨ
 F = W sin α
 N = W cos α
For angles less than 10°, sin α ≈ tan α (the small
–angle assumption); with that substitution:
 F = W tan α but
 tan α =
𝑉
𝐻
&
𝑉
𝐻
= G%

30. Grade Resistance
 The force-opposing movement of a machine up a frictionless
slope is known as grade resistance.
 It acts against the total weight of the machine, whether track type
or wheeltype.
 When a machine moves up an adverse slope, the power required to
keep it moving increases approximately in proportion to the
slope of the road.

31. Grade Resistance
 The most common method of expressing a slope is by gradient in
percent.
 A 1% slope is one where the surface rises or drops 1 ft. vertically in
a horizontal distance of 100ft.
 If the slope is 5%, the surface rises or drops 5 ft. per 100 ft. of
horizontal distance.
 If the surface rises, the slope is defined as plus, whereas if it
drops, the slope is defined as minus.

32. Rim pull
 Rim pull is a term that is used to designate the tractive force between
the tires of machine’s driving wheels and the surface on which they
travel.
 If the coefficient of traction is sufficiently high there will be no tire
slippage, in which case maximum rim pull is a function of the power of
the engine and the gear ratios between the engine and the driving
wheels.
 If the driving wheels slip on the supporting surface, the maximum
effective rim pull will be equal to the total pressure the tires exert on
the surface multiplied by the coefficient oftraction.

33. Coefficient of Traction
The factor that determines the maximum possible
tractive force between the powered running gear of a
machine and the surface on which it travels.

34. Rim Pull Equation
Rim Pull = 375 * hp * efficiency(lb)
speed (mph)
The efficiency of most tractors and trucks will range
from 0.80 to 0.85 (use 0.85 if efficiency is notknown).

35. Drawbar Pull
 The towing forcea crawlertractorcan exert on a load is
referred to as drawbarpull.
 Drawbar pull is typically expressed inpounds.
 Todetermine thedrawbarpull available for towing a
load it is necessary to subtract from the total pulling
force available at the engine the force required to
overcome the total resistance imposed by the haul
conditions.
 If a crawler tractor tows a load up a slope, its drawbar
pull will be reduced by 20 lb for each ton of weight of
the tractor for each 1%slope.

37. Usable Power
 Usable power depends on project conditions:
primarily, haul-road surface condition, altitude,and
temperature.
Usable force = Coefficient of traction * Weighton
powered runninggear

38. Grade Resistance
• Grade resistance represents that component
of vehicle weight which acts parallel to an
inclined surface.
– When the vehicle is traveling up a grade, grade
resistance is positive.
– When traveling downhill, grade resistance is
negative.

39. 5 ft
100 ft
5%100
ft100
ft5

Grade Resistance

40. Grade Resistance
• The exact value of grade resistance may be found
by multiplying the vehicle's weight by the sine of
the angle that the road surface makes with the
horizontal.
• For the grades usually encountered in
construction, it is sufficiently accurate to use the
approximation of Equation 4-4.
– Grade resistance factor (lb/ton) =20 × grade (%)
(4-4A)
– Grade resistance factor (kg/t) =10 × grade (%)
(4-4B)

41. Grade Resistance
• That is, a 1% grade (representing a rise of 1
unit in 100 units of horizontal distance) is
considered to have a grade resistance equal to
1% of the vehicle's weight.
– This corresponds to a grade resistance factor of 20
lb/ton (10 kg/t) for each 1% of grade,

42. Grade Resistance
• Grade resistance (lb or kg) may be calculated
using Equation 4-5 or 4-6.
– Grade resistance (lb) = Vehicle weight (tons) ×
Grade resistance factor (lb/ton) (4-5A)
– Grade resistance (kg) =Vehicle weight (t) × Grade
resistance factor (kg/t) (4-5B)
– Grade resistance (lb) =Vehicle weight (lb) × Grade
(4-6A)
– Grade resistance (kg) =Vehicle weight (kg) x Grade
(4-6B)

43. Effective Grade
• The total resistance to movement of a vehicle
– (the sum of its rolling resistance and grade
resistance)
– might be expressed in pounds or kilograms.
• OR expressing total resistance is to state it as a
grade (%),
– A grade resistance equivalent to total resistance
actually encountered.

44. Effective Grade
• Effective grade may be easily calculated by use
of Equation 4-7.
– Effective grade (%) = Grade (%) + Rolling resistance
factor (lb/ton)/20 (4-7A)
– Effective grade (%) =Grade (%) + Rolling resistance
factor (kg/t)/10 (4-7B)

45. EXAMPLE 4-1
• A wheel tractor-scraper weighing 100 tons (91
t) is being operated on a haul road with a tire
penetration of 2 in. (5 cm).
• What is the total resistance (lb and kg) and
effective grade when
– (a) the scraper is ascending a slope of 5%;
– (b) the scraper is descending a slope of 5%?

46. EXAMPLE 4-1
• Solution
Rolling resistance factor = 40 + (30 × 2) =100 lb/ton
[= 20 + (6 × 5) =50 kg/t]
Rolling resistance = 100 (lb/ton) × 100 (tons) = 10,000 lb
[= 50 (kg/t) × 91 (t) = 4550 kg]
(a) Grade resistance = 100 (tons) × 2000 (lb/ton) × 0.05
= 10,000 lb
[= 91 (t) x 1000 (kg/t) × 0.05 =4550 kg]
Total resistance = 10,000 lb + 10,000 lb = 20,000 lb
[= 4550 kg + 4550 kg = 9100 kg]

47. EXAMPLE 4-1
Effective grade =5 + 100/20 =10%
(b) Grade resistance =100 (tons) × 2000(lb/ton)× (-
0.05) = -10,000 lb
[= 91 (t) × 1000 (kg/t) x (-0.05) =-4550 kg]
Total resistance = -10,000 lb + 10,000 lb = 0 lb
[= -4550 kg + 4550 kg = 0 kg)
Effective grade = -5 + 100/20 = 0%
[= -5 + 50/10 = 0%]

48. EXAMPLE 4-2
• A crawler tractor weighing 80,000 lb (36 t) is
towing a rubber-tired scraper weighing
100,000 lb (45.5 t) up a grade of 4%. What is
the total resistance (lb and kg) of the
combination if the rolling resistance factor is
100 lb/ton (50 kg/t)?

49. EXAMPLE 4-2
• Solution
Rolling resistance (neglect crawler) = 100 000 (lb)
/2000 (lb/ton) × 100 (lb/ton) = 5000 lb
[=45.5 (t) × 50 (kg/t) =2275kg]
Grade resistance = 180,000 × 0.04 = 7200 lb (4-6A)
[= 81.5 × 1000 kg/t × 0.04 = 3260 kg] (4-6B)
Total resistance = 5000 + 7200 = 12,200 lb
[= 2275 + 3260 = 5535 kg] (4-2)

50. Effect of Altitude
• All internal combustion engines lose power as
their elevation above sea level increases
because of the decreased density of air at
higher elevations.
• Engine power decreases approximately 3% for
each 1000 ft (305 m).

51. Effect of Altitude
• Turbocharged engines are more efficient at
higher altitude than are naturally aspirated
engines and may deliver full rated power up to
an altitude of 10,000 ft (3050 m) or more.

52. Effect of Altitude
• When derating tables are not available,
– the derating factor obtained by the use of Equation 4-
8 is sufficiently accurate for estimating the
performance of naturally aspirated engines.
– Derating factor (%) = 3 × [(Altitude (ft) - 3000*)/1000
(4-8A)
– Derating factor (%) = (Altitude (m) - 915*)/102
(4-8B)
*Substitute maximum altitude for rated performance, if
known.

53. Effect of Altitude
– The percentage of rated power available
= 100 - the derating factor.

54. Effect of Traction
• The power available to move a vehicle and its
load is expressed as :
– rimpull for wheel vehicles and
– drawbar pull for crawler tractors.

55. Effect of Traction
• Rimpull is :
– the pull available at the rim of the driving wheels
under rated conditions.
– Also, the power available at the surface of the
tires.
• Drawbar pull is :
– the power available at the hitch of a crawler
tractor operating under standard conditions.

56. Effect of Traction
• Factors affect maximum pull of Vehicle are:
a) Operation at increased altitude may reduce the
maximum pull of a vehicle,
• as explained in the previous slides.
b) the maximum traction that can be developed
between the driving wheels or tracks and the
road surface.
Maximum usable pull = Coefficient of traction × Weight on drivers
(4-9)
o This represents the maximum pull that a vehicle
can develop, regardless of vehicle horsepower

57. Effect of Traction
• For crawler tractors and all-wheel-drive
rubber-tired equipment,
– the weight on the drivers is the total vehicle
weight.

58. TABLE 4-2: Typical values of coefficient of Traction

59. EXAMPLE 4-3
• A four-wheel drive tractor weighs 44,000 lb
(20000 kg) and produces a maximum rimpull of
40,000 lb (18160 kg) at sea level.
• The tractor is being operated at an altitude of
10,000 ft (3050 m) on wet earth.
• A pull of 22,000 lb (10000 kg) is required to move
the tractor and its load.
• Can the tractor perform under these conditions?
– Use Equation 4-8 to estimate altitude deration.

60. EXAMPLE 4-3
• Solution
Derating factor = 3 × [(10000 – 3000)/1000]
= 21% (4-8A)
[ = (3050 915)/102 =21%] (4-8B)
Percent rated power available=100 21 = 79%
Maximum available power = 40,000 × 0.79
= 31,600 lb
[ = 18160 × 0.79 = 14346 kg]

61. EXAMPLE 4-3
Coefficient of traction =0.45 (Table 4-2)
Maximum usable pull =0.45 × 44,000 = 19,800lb
(4-9)
[= 0.45 × 20000 = 9000 kg]

62. EXAMPLE 4-3
• Note on Example 4-3:
– Because the maximum pull as limited by traction is
less than the required pull, the tractor cannot
perform under these conditions.
– For the tractor to operate, it would be necessary to:
• reduce the required pull (total resistance),
• increase the coefficient of traction, or
• increase the tractor's weight on the drivers.

63. Loading and Hauling
• EXAMPLE
– A wheel tractor-scraper weighing 91 t is being operated on a
haul road with a tire penetration of 5 cm. What is the total
resistance kg and effective grade when (a) the scraper is
ascending a slope of 5%; (b) the scraper is descending a slope of
5%?
SOLUTION

64. Loading and Hauling

65. Loading and Hauling
• EXAMPLE
– A crawler tractor weighing 36 t is towing a rubber-tired scraper
weighing 45.5 t up a grade of 4%. What is the total resistance kg
of the combination if the rolling resistance factor is 50 kg/t?SOLUTION