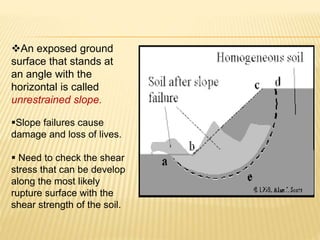
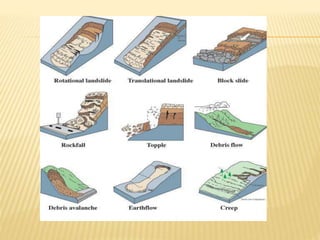
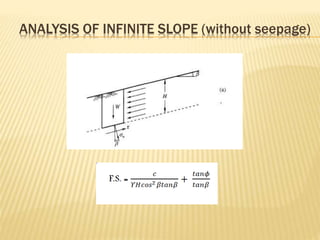
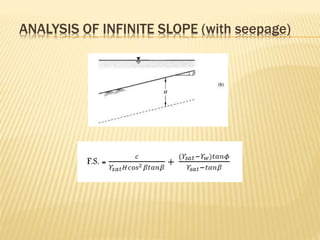
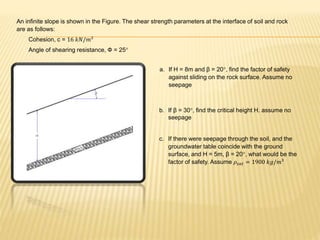
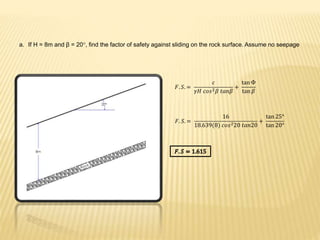
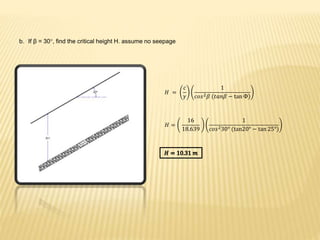
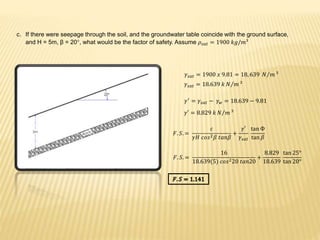
The document discusses slope stability and factors that influence it. It defines an unrestrained slope and describes different types of slope failures such as base failure and midpoint circle failure depending on where the surface of sliding intersects the slope. Factors that influence slope stability include soil/rock strength, groundwater, external loading, slope geometry. Slope failures can be triggered by erosion, rainfall, earthquakes, construction activities, and more. Methods to improve slope stability include flattening slopes, adding weight/retaining walls, lowering the water table, soil improvement. Stability analysis procedures include mass and methods of slices approaches. The factor of safety is defined and equations for infinite slope analysis with and without seepage are provided.

1. SLOPE STABILITY

2. An exposed ground
surface that stands at
an angle with the
horizontal is called
unrestrained slope.
Slope failures cause
damage and loss of lives.
 Need to check the shear
stress that can be develop
along the most likely
rupture surface with the
shear strength of the soil.

3. TYPES OF SLOPE FAILURES

7. MODES OF FAILURE
 When the surface of sliding intersects the slope
at or above its toe,
 when the surface of sliding passes at some
distance below the toe of the slope,
the failure is called,
Slope of failure
base failure
midpoint circle

8. FACTORS THAT INFLUENCE SLOPE STABILITY
 Soil and rock strength
 Discontinuities and planes of weakness
 Groundwater and seepage
 External loading
 Slope geometry

9. TRIGGERING FACTORS (CAUSES OF SLOPE FAILURE)
 erosion
 Rainfall
 Earthquakes
 Geological factors
 External loading
 Construction activities
 Increment of pore water pressure
 Change in topography

10. METHODS TO IMPROVE AND PROTECT SLOPE
STABILITY
 Slopes flattened or benched
 Weight provided at toe
 Lowering of groundwater table to reduce pore
water pressures in the slope
 Use of driven / cast in place piles
 Retaining wall or sheet piling provided to
increase resistance to sliding
 Soil improvement

11. TYPES OF STABILITY ANALYSIS PROCEDURES
 Mass Procedure – The mass of the soil above the
surface of sliding is taken as a unit.
 Methods of Slices – The soil above the surface of
sliding is divided into a number of vertical parallel
slices.
o The stability of each slice is calculated separately.
o Non-homogeneity of the soils and pore water pressure
can be taken into consideration.
o It also accounts for the variation of the normal stress
along the potential failure surface.

12. FACTOR OF SAFETY
𝐹𝑆 =
𝜏 𝑓
𝜏 𝑑
Where:
FS = factor of safety
𝞽f = shear strength
𝞽d = shear stress

13. Cohesion and Friction may be expressed as,
𝜏 𝑓 = 𝑐′ + 𝜎′𝑡𝑎𝑛𝛷′
Where:
c’ = cohesion
𝜱’ = angle of friction
𝝈’ = effective normal stress
We can also use,
𝜏 𝑑 = 𝑐′ 𝑑 + 𝜎′𝑡𝑎𝑛𝛷′ 𝑑

14. By substituting the equations,
𝐹. 𝑆. =
𝑐′ + 𝜎′𝑡𝑎𝑛𝛷′
𝑐′ 𝑑 + 𝜎′𝑡𝑎𝑛𝛷′ 𝑑
Factor of safety with respect to cohesion,
𝐹𝑆𝑐′ =
𝑐′
𝑐′ 𝑑
Factor of safety with respect to friction,
𝐹𝑆 𝛷′ =
𝑡𝑎𝑛𝛷′
𝑡𝑎𝑛𝛷′ 𝑑

15. When those three equations are compared,
Or,
𝐹𝑆 = 𝐹𝑆𝑐′ = 𝐹𝑆 𝛷′
When FS is equal to 1, the slope is in state of
impending failure.
A value of 1.5 for the FS with respect to
strength is acceptable for the design of a stable
slope.
𝑐′
𝑐′ 𝑑
=
𝑡𝑎𝑛𝛷′
𝑡𝑎𝑛𝛷′ 𝑑

16. ANALYSIS OF INFINITE SLOPE (without seepage)

17. ANALYSIS OF INFINITE SLOPE (without seepage)
Max. height of the slope for which
critical equilibrium occurs

18. ANALYSIS OF INFINITE SLOPE (with seepage)

19. What will be the factors of safety with respect to average shearing strength, cohesion and
internal friction of a soil, for which the shear strength parameters obtained from the laboratory
test are c´ = 32 kN/m2 and Ø´ = 18°, the expected parameters of mobilized shearing resistance
are c´α= 21 kN/m2 and Ø´α = 13° and the average effective pressure on the failure plane is 110
kN/m2 . For the same value of mobilized shearing resistance determine the following:
1. Factor of safety with respect to strength
2. Factor of safety with respect to friction when that with respect to cohesion is unity;
and
3. Factor of safety with respect to strength.

20. SOLUTION:
1. Factor of safety with respect to strength
𝜏f = c´ + σ´ tanØ ´ τα = c´ α + σ´ tanØ ´α
= 32 + 110tan18° = 21 + 110tan13°
= 67.8 kN/m2 = 46.4 kN/m2
FACTOR OF SAFETY =
𝜏f
𝜏α
=
67.8 𝑘𝑁/𝑚2
46.4 𝑘𝑁/𝑚2 = 𝟏. 𝟒𝟔

21. SOLUTION:
2. Factor of safety with respect to friction
FACTOR OF SAFETY =
tan Ø′
𝑡𝑎𝑛Øα
=
𝑡𝑎𝑛18°
𝑡𝑎𝑛13°
= 1.41
Factor of safety with respect to cohesion
FACTOR OF SAFETY =
𝑐′
𝑐 𝛼
=
32
21
= 1.52

22. SOLUTION:
3. Factor of safety with respect to height
FH = Fc Will be at FØ = 1.0
τα = 46.4 =
32
F 𝑐
+
110𝑡𝑎𝑛18°
1.0 , therefore F𝑐 =
32
46.4−35.8
= 3.0
Factor of safety with respect to friction at FØ = 1.0 is
τα = 46.4 =
32
1.0
+
110𝑡𝑎𝑛18°
FØ
, therefore, FØ =
35.8
46.4−32
= 2.49
Factor of safety with respect to strength Fs is obtained when FØ = Fc we may write;
τα = 46.4 =
32
Fs
+
110𝑡𝑎𝑛18°
Fs
, OR Fs = 1.46

23. An infinite slope is shown in the Figure. The shear strength parameters at the interface of soil and rock
are as follows:
Cohesion, c = 16 𝑘𝑁/𝑚²
Angle of shearing resistance, Ф = 25°
a. If H = 8m and β = 20°, find the factor of safety
against sliding on the rock surface. Assume no
seepage
b. If β = 30°, find the critical height H. assume no
seepage
c. If there were seepage through the soil, and the
groundwater table coincide with the ground
surface, and H = 5m, β = 20°, what would be the
factor of safety. Assume 𝜌𝑠𝑎𝑡 = 1900 𝑘𝑔/𝑚³

24. a. If H = 8m and β = 20°, find the factor of safety against sliding on the rock surface. Assume no seepage
𝐹. 𝑆. =
𝑐
𝛾𝐻 𝑐𝑜𝑠2 𝛽 𝑡𝑎𝑛𝛽
+
tan Ф
tan 𝛽
𝐹. 𝑆. =
16
18.639(8) 𝑐𝑜𝑠220 𝑡𝑎𝑛20
+
tan 25°
tan 20°

25. b. If β = 30°, find the critical height H. assume no seepage
𝐻 =
𝑐
𝛾
1
)𝑐𝑜𝑠2 𝛽 (𝑡𝑎𝑛𝛽 − tan Ф
𝐻 =
16
18.639
1
𝑐𝑜𝑠230° (tan )20° − tan 25°

26. c. If there were seepage through the soil, and the groundwater table coincide with the ground surface,
and H = 5m, β = 20°, what would be the factor of safety. Assume 𝜌𝑠𝑎𝑡 = 1900 𝑘𝑔/𝑚³
𝛾𝑠𝑎𝑡 = 1900 𝑥 9.81 = 18, 639 𝑁 𝑚 ³
𝛾𝑠𝑎𝑡 = 18.639 𝑘 𝑁 𝑚 ³
𝛾′
= 𝛾𝑠𝑎𝑡 − 𝛾 𝑤 = 18.639 − 9.81
𝛾′ = 8.829 𝑘 𝑁 𝑚 ³
𝐹. 𝑆. =
𝑐
𝛾𝐻 𝑐𝑜𝑠2 𝛽 𝑡𝑎𝑛𝛽
+
𝛾′
𝛾𝑠𝑎𝑡
tan Ф
tan 𝛽
𝐹. 𝑆. =
16
18.639(5) 𝑐𝑜𝑠220 𝑡𝑎𝑛20
+
8.829
18.639
tan 25°
tan 20°

27. REPORTERS:
Arellano, Raciel M.
Barcelon, Lennie A.
Cabico, Mary Joy S.
Diaz, Mary Jasmin W.
Garcia, Michelle A.
Llanos, Melody P.
Moreno, Rina M.
Poblete, Jewelette Anne U.
Policarpio, Shyne
Toquia, Rachel P.
Venturero, Alecxei T.
Villanueva, Alvin T.

28. REFERENCES:
 Geotechnical Engineering by Braja M. Das
 Fundamentals of Geotechnical Engineering
by DIT Gillesania
 http://people.eng.unimelb.edu.au/stsy/geome
chanics_text/Ch11_Slope.pdf
 http://web.itu.edu.tr/~teymurb/fe1lecture3.pdf