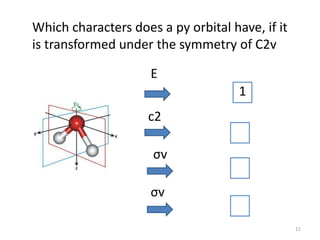
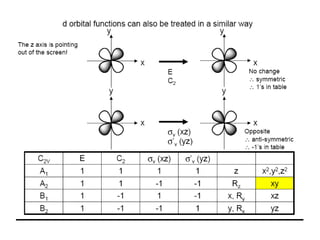
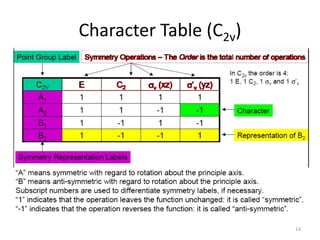
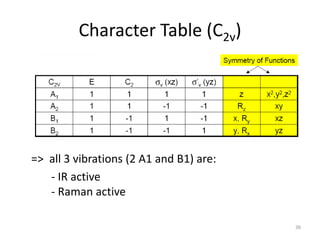
The document covers the fundamentals of symmetry operations, point groups, and representations in molecular properties such as vibrations and orbitals. It explains how to determine character tables for specific molecules and the significance of irreducible representations in understanding molecular behavior under these symmetry operations. Additionally, it discusses applications of group theory in predicting molecular vibrations and hybridization in various chemical contexts.

1. Character Tables
Dr. Christoph
Phayao University Nov.2013
1

2. What’s this lesson about ?
• Review Symmetry Operations
• Review Point Groups
• “Representations”
or: symmetry of molecule properties
(vibrations, orbitals)
• Reducing representations
2

3. Tetrahedral Td Octahedral Oh
Linear: D∞h for A-B-A ( i )
C ∞h for A-B
http://en.wikibooks.org/wiki/Introduction_to_Mathematical_Physics/N_body_problem_in_quantum_mechanics/Molecules
3

4. Determine the point groups of these molecules:
2 4
5 6 7
1
3
4

5. “Representations”
Each symmetry operation transforms a molecule to
look the same as before
(s. molwave.com simulation)
For example:
C2 axis and 2 σv mirrors
BUT: a symmetry operation transforms parts of a
molecule in different ways !
5

6. For example:
The z-axis of a C2v molecule remains unchanged
for all symmetry operations.
We call this element “totally symmetric” and this
is represented by the symbol A and “1” for every
operation:
http://www.webqc.org/symmetrypointgroup-c2v.html
6

7. Now we look at the x-axis of the water molecule – how
does it behave by all the symmetry operations ?
• E leaves it unchanged => “1” character
• C2 reverses the x-axis => “-1” character
• Reflection in the xz plane leaves it unchanged => “1”
• but reflection on the yz plane reverses it => “-1”
We call this behavior (antisymmetric to Cn) as “B”
7

8. 8

9. ผลของการดาเนินการเกี่ยวกับ C2 PX วงโคจรคืออะไร?
9

10. 10

11. Which characters does a py orbital have, if it
is transformed under the symmetry of C2v
11
E
c2
σv
σv
1

14. Character Table (C2v)
14

15. Example: C4v
What are the characters for the z-axis for each
symmetry operation ?
E 2C4 C2 2 σv 2 σd
15
But how about x- and y-axis ??

16. C4 operation
y
x
The x-value becomes the y-value
y
x
The y-value becomes the
negative x-value
=> (x, y)  (y, -x)
16

17. “Representations” of C4
In difference to the z-axis, the x- and y- axis are transformed into
“something” else (x becomes y, y becomes –x).
How about the characters here ?
We cannot use simple “1”and “-1” anymore !
Instead the characters are “0” for both x- and y-axis under C4 !
[ for advanced users: the characters are the trace of the
transformation matrix, which transforms the point (x, y) to (y, -x):
17

18. C4v: characters of x- and y-axis
18
E 2C4 C2 2 σv 2 σd
X- and y-axis are “degenerated”, they have the
same behaviour !
=> This set of characters is a irreducible
representation already and is called “E” (not to
confuse with identity E !)

19. Character Table for C4v
19
Find all character tables here:
http://www.webqc.org/symmetry.php
s and pz orbitals
dz2 orbital
dx2-y2 orbital
dxy orbital
px and py orbitals

20. Character Table Representations
1. Characters of +1 indicate that the basis function is
unchanged by the symmetry operation.
2. Characters of -1 indicate that the basis function is
reversed by the symmetry operation.
3. Characters of 0 indicate that the basis function
undergoes a more complicated change.

21. Character Table Representations
1. An A representation indicates that the
functions are symmetric with respect to
rotation about the principal axis of rotation.
2. B representations are asymmetric with
respect to rotation about the principal axis.
3. E representations are doubly degenerate.
4. T representations are triply degenerate.
5. Subscrips u and g indicate asymmetric
(ungerade) or symmetric (gerade) with
respect to a center of inversion.

22. B R E A K
22

23. “Reducible Representations”
The representations in the character tables are the
basic characters for each symmetry operation.
In reality we often have a combination of these !
23

24. Example: H orbitals in water
The H1 atom is different from the H2 atom !
How do these 2 atoms as H-1s AO transform
under the operations in C2v ?
24

25. A transformation (using a specific symmetry operation)
is called “ Γ “
Γ =
AO 2AO1
25

26. “Reduction”
The representation for the 2 bonds must be “reduced”
to the basic representations of the C2v point group !
Γ = 2 0 2 0
A1
B1
+
=> The 2 bonds are a combination of A1 and B1 representation
26

27. “Reduction” Formula – if we cannot see by just testing:
# A1 = (1/4) * [ (2 * 1 *1) + (0) + (2 * 1 *1) + (0) ] = 1
=> Γ contains 1x A1
# B1 = (1/4) * [ (2 *1 *1) + (0) + (2 *1 *1) ] = 1
=> Γ contains 1x B1
27
Г = 2 0 2 0
h = 4

28. What can we read out
of character tables ?
28

29. Applications of Group Theory
1. Determining the symmetry properties
of all molecular motion (rotations,
translations and vibrations).
Group theory can be used to predict
which molecular vibrations will be seen
in the infrared or Raman spectra.
For IR: we have 3N-6 modes in a molecule
(3N – 5 in a linear molecule)

30. IR vibrations in H2O
30
Find the characters of all x/z/y coordinates for each atom:
Under C2: only O-z-axis remains (= +1)
x1 and y1 reversed (= -2)
all other coordinates go elsewhere
=> character is: 1-2 = -1
Find the remaining characters for σv and σv’
1

31. Reduce the representation for coordinates
31
For the water molecule, Γvib = Γcart - Γtrans - Γrot =
{3A1 + A2 + 3B1 + 2B2} - {A1 + B1 + B2} - {A2 + B1 + B2} = 2A1 + B1
2

32. Projection Operator
Shape of the functions
32
We get 2 A1 vibrations and 1 B1 vibration
3
What happens to one x/y/z coordinate set under the symmetry operations ?
E C2 σv σv’
x1  x1 -x2 x1 -x2
y1  y1 -y2 -y1 y2
z1  z1 z2 z1 z2
Multiply with characters:
P(A1)(x1) = 2 x1 -2 x2 P(A1)(y1) = 0 P(A1)(z1) = 2 z1 + 2 z2
 x1 – x2 and z1 + z2 for A1
P(B1)(x1) = x1 + x2 P(B1)(y1) = 0 P(B1)(z1) = z1 – z2

33. All vibration modes of water
33

34. Molecular Vibrations
For a molecular vibration to be seen in
the infrared spectrum (IR active), it must
change the dipole moment of the
molecule. The dipole moment vectors
have the same symmetry properties as
the cartesian coordinates x, y and z.

35. Molecular Vibrations
For a molecular vibration to be seen in
the Raman spectrum (Raman active), it
must change the polarizability of the
molecule. The polarizability has the
same symmetry properties as the
quadratic functions:
xy, yz, xz, x2, y2 and z2

36. Character Table (C2v)
=> all 3 vibrations (2 A1 and B1) are:
- IR active
- Raman active
36

37. CO IR vibrations
We compare cis- and trans-ML2(CO)2 complexes in IR:
What are the point groups ?
37

38. Character Tables for cis and trans
38

39. Representations of 2 C-O groups
Which contains the irreducible representations :
Which contains the irreducible representations :
Conclusion: Number of IR peaks for cis and trans complex:
39

40. Applications of Group Theory
2. Predicting the orbitals used in group
orbitals. Group orbitals result from the
combining or overlap of atomic orbitals,
and they include the entire molecule.

41. H-AO’s in Water
41
Remember that we found that the 2 H orbitals
have the representations A1 + B1.
How do these combinations look like ?

42. Use “projection operator”
42
How does each H-orbital
transform under c2v ?
E C2 σv σv’
H1 H2 H1 H2
Multiply with the
characters:
 P(A1)(H1) = 2 H1 + 2 H2
 normalized: H1 + H2
 P(B1)(H1) = 2 H1 – 2 H2
 normalized: H1 – H2
These are
the 2 group
orbitals of H
in water

43. Applications of Group Theory
3. Predicting the orbitals used in σ bonds.
Group theory can be used to predict
which orbitals on a central atom can be
mixed to create hybrid orbitals.

44. Hybridization
• Determine the hybridization of boron in BF3.
The molecule is trigonal planar, and belongs to
point group D3h.
1. Consider the σ bonds as vectors.
Fa
B Fc
Fb
44

45. Hybridization
Determine how each vector (σ bond) is transformed
by the symmetry operations of the group.
45

46. Determining Hybridization
E 2C3 3C2 σh 2S3 3σv
Гred
46

47. Determining Hybridization
E 2C3 3C2 σh 2S3 3σv
Гred 3 0 1 3 0 1
47

48. “Reduction” of Гred
# A1’ = 1/12 *
[ ( 3 * 1 * 1) + ( 0) + (1 * 1 * 3) +
( 3 * 1 * 1) + (0) + ( 1 *1 *3)] = 1
Try the same method for A2’ and E’ !
48

49. “Reduction”
This is a reducible representation, so use character table to reduce it.
D3h E 2C3 3C2 σh 2S3 3σv
Г 3 0 1 3 0 1
#A1’ = (1/12) [ 3 + 0 + 3 + 3 + 0 + 3] = 1
#A2’ = (1/12) [ 3 + 0 - 3 + 3 + 0 - 3] = 0
…
#E’ = (1/12) [ 6 + 0 + 0 + 6 + 0 + 0] = 1
Г = A1’ + E’
Which orbitals belong to these symmetry species?
A1’ = s-orbital
E’ = 2 p-orbitals
Therefore, it is an sp2 hybrid orbital 49

50. Hybridization of BF3
Гred reduces to A1′ + E ′. The orbitals used in
hybridization must have this symmetry.
Which orbitals of Boron are involved in the bonding ?
(Consider that the d-orbitals are too high in energy to be used
for Boron !)
50

51. Degenerated Representations
Double degeneration = E (not confuse with identity”E” !!)
Triple degeneration = T
Example: D3h group has two representations “E”
51

52. Degeneration of x and y
We have to combine the 2 points into 1 matrix
and find the trace of the matrix (here: 2)
52

53. Degeneration x and y
53
For the C3 operation we can use the ROTATION MATRIX:
For 120 deg, the trace of the rotation matrix becomes -1 !

54. Summary: Character Tables
Molecule belongs to a symmetry point group if it is unchanged
under all the symmetry operations of this group.
Certain properties of the molecule (vibrational, electronic and
vibronic states, normal vibrational modes, orbitals) may behave
the same way or differently under the symmetry operations of
the molecule point group. This behavior is described by the
irreducible representation (irrep, character). All irreducible
representations of the symmetry point group may be found in
the corresponding character table.
Molecular property belongs to the certain irreducible
representation if it changes under symmetry operations exactly
as it is specified for this irreducible representation in the
character table. 54

55. Special notations
Mulliken Symbol Interpretation
a
Non-degenerate orbital;
symmetric to principal Cn
b
Non-degenerate orbital;
unsymmetric to principal Cn
e Doubly degenerate orbital
t Triply degenerate orbital
(subscript) g
Symmetric with respect to
center of inversion
(subscript) u
Unsymmetric with respect to
center of inversion
(subscript) 1
Symmetric with respect to
C2 perp. to principal Cn
(subscript) 2
Unsymmetric with respect to
C2 perp. to principal Cn
(superscript) ' Symmetric with respect to sh
(superscript) " Unsymmetric with respect to sh
55

56. Exercise: IR modes of H2O
56
Rule: 3N – 5 vibrations for linear molecules
3N – 6 vibrations for non-linear
Determine the behaviour of the INTERNAL coordinates of
the molecule (bonds and bond angles) :

57. Reducing Г
57
# A1 = ¼ [ (3) + (1) + (3) + (1) ] = 2
# B1 = ¼ [ (3) + (-1) + (3) + (-1) ] = 1

58. Basis functions
58
How do these vibrations look like ?
r1 -> r1 r2 r1 r2
r2 -> r2 r1 r2 r1
Ѳ -> Ѳ Ѳ Ѳ Ѳ
Under A1 multiply each with 1: ф1 = 2(r1+r2)
ф2 = 4 Ѳ
Under B1 multiply each with 1 / -1 / 1 / -1:
ф3 = 2(r1-r2)