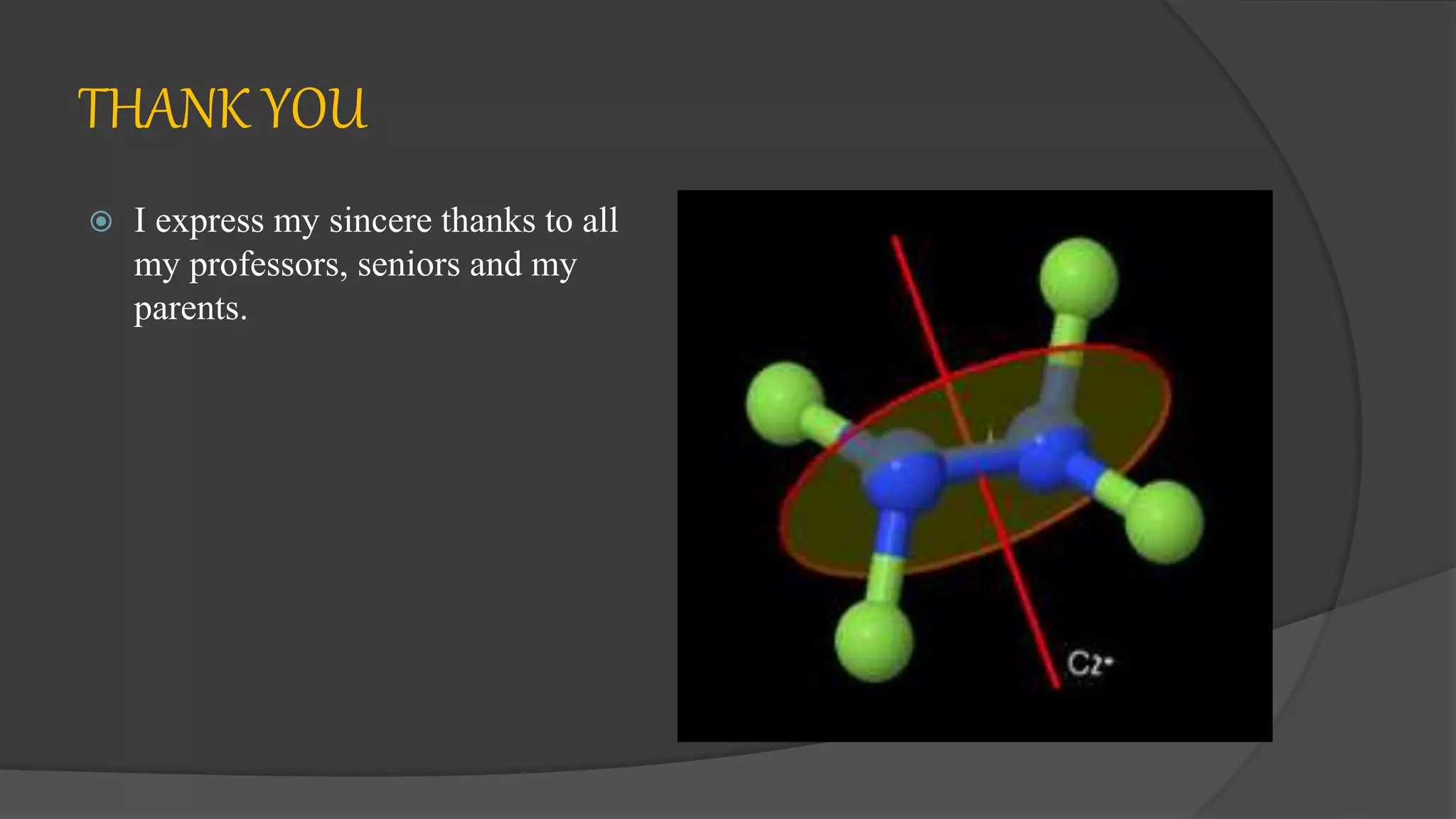
This document summarizes a seminar on group multiplication tables and abelian/non-abelian point groups. It defines groups, subgroups, symmetry operations, and point groups. It provides examples of group multiplication tables for C2v and C3v point groups. Abelian groups have commutative combinations while non-abelian groups like C3v do not. Low, high, and special symmetry molecule types are classified by their point groups. Examples are given throughout to illustrate key concepts.

1. SEMINAR ON
GROUP MULTIPLICATION TABLES
&
ABELIAN , NON-ABELIAN POINT GROUPS
BY
MISS. NEHA MILIND DHANSEKAR
MSc I ANALYTICAL CHEMISTRY
THE INSTITUTE OF SCIENCE
15, MADAM CAMA RAOD.

2. CONTENTS
Concept of groups
Sub – group
Classes of Symmetry Operations
Group Multiplication table
Abelian & Non Abelian Point Group
Point group

3. QUESTIONS
 Explain abelian and non-abelian point group using
suitable example for each. [4 marks ] { nov’ 17 ; june
18 }
 Define subgroup . Give its characteristic [ 3 marks ]
{ June 18 }

4. GROUPS
 A molecule may have different element of symmetry such as axis of
symmetry (Cn), plane of symmetry (σ) etc.
 A collection of all these elements of symmetry constitute a “ Symmetry
group”.
 In a molecule when at least one point is fixed for all these symmetry
operations to carry out , then the symmetry group called “ Point Group”.
 Complete set of symmetry elements “A , B ,C ” form a mathematical group
“ G ” and hence to form “G”, following condition must be satisfied.

5. 1.Two elements in a group (A&B) combines to form a third element called C and this
C belongs to the element of group .
A.B=C
2 An element combine itself to form the another element of group.
i.e A.A =E (exception)
A.A = B ( another element of group )
3. Group must contain identity element [E] which commute with other element
keeping them unchanged.
i.e. A.E =E.A = A
Similarly, B.E = E.B = B etc.
e.g . In H2O ; ( C2V)⇒ E.C2 = C2 =C2.E
4. Every element of group “Associative law of combinations”.
A(BC) =( AB)C
e.g . In H2O ; ( C2V)⇒ E (C2.σv) = (E.C2)σv = σ’v

6. 5.For every A in group ,there is A⁻¹ exist and when both are carried
out in succession , the resultant effect is identify transformation.
AA⁻¹=A⁻¹A=E
 Order of Group( h ) :
 It is a total no. of element in group .

7. SUB – GROUPS
 Among the operations that constitute a point group , there
generally exist smaller sets that also obey 4- requirements of a
group .
 The smaller sets which are groups in their own right , can be
considered as sub – groups of larger group. From which the
elements were carried .
 Group ⇒ h ( order) & sub – group ⇒ g(order )
then ‘g’ must be deviser of ‘h’
i.e h/g = k = Some integral

8. e.g. C2v ⇒ { E , C2 ,σ’v ,σ’’v }
 Group ⇒ C2v
 & Subgroups ⇒ { E } ⇒ C1
{ E , C2 } ⇒ C2
{ E , σ’v } ⇒ Cs
{ E , σ’’v } ⇒ Cs
Thus C1 , C2 & Cs are the sub- groups of group C2v .

9. CLASSES OF SYMMETRY OPERATIONS
 “ A set of elements in a group which are conjugate to one
another is said to form a class”.
 Two elements say A & B in a group forms a class if they are
conjugate and they are related as follows ;
 X⁻¹AX = B
 Where ; x = another element of group .
 E.g. Similarity transformation of C2 operation of H2O molecule
with all other operations .

10. C2V – { E , C2, σv , σ’v}
Table : E ⁻¹C2E= C2 ;
(C2) ⁻¹C2 (C2)=C2
(σv ) ⁻¹ C2 (σv )=C2
(σ’v) ⁻¹C2 σ’v = C2
Since E ⁻¹.E = (C2) ⁻¹.C2= (σv ) ⁻¹(σv )= (σ’v) ⁻¹ σ’v =E
&E.C2=C2
From this we can say that ,

11. • C2 belongs to seperate class since similarity
transformation of C2 with all separation generates C2
 Asymmetry operation which commute with all
symmetry operation belong to separate class. Hence in
Abelian group every symmetry operation belongs to
separate class .

12. GROUP MULTIPLICATION TABLE
 A multiplication table is an array showing the result of applying a
binary operation to the element of the given set .
Thus the table that reveals the relation between the elements of a
group and hence called “ Group Multiplication Table” .
 E.g 1. H2O belongs to (C2v) point group with E , C2 , σv
& σ’v as the symmetry elements .

13. C2v
C2v E C2 σv σ’v
E E C2 σv σ’v
C2 C2 E σ’v σv
σv σv σ’v E C2
σ’v σ’v σv C2 E
σv(xz) σv(yz)

15. C3v
C3V E C3¹ C3² σv σ’v σ’’v
E E C3¹ C3² σv σ’v σ’’v
C3¹ C3¹ C3² E σ’v σ’’v σv
C3² C3² E C3¹ σ’’v σv σ’v
σv σv σv σ’v E C3² C3¹
σ’v σ’v σ’v σ’’v C3¹ E C3²
σ’’v σ’’v σ’’v σv C3² C3¹ E

16. Abelian & Non –Abelian Point Group
 Definition : In mathematics of group , any group in which
all combinations of elements commute. This group is said
to be “ Abelian Group”.
 By associavity : The associative law of combination is valid
for combinations of elements of the group .
Thus , for example in C2v(H2O) ⇒ { E , C2 ,σ’v ,σ’’v }
 Account to commutation an associative law :
C2v ⇒ C2 (σ’v.σ’’v )=(C2 .σ’v) σ’’v

17. If the product two elements or operations of point groups is not commutative
then point group is called Non – Abelian Point group .
i.e. AB ≠ BA
E.g. NH3 ⇒ C3V = { E , C3 , C3², σv , σ’v , σ’’v }
 σv.C3²≠C3².σv

18. Point group
 “ Collection of a symmetry elements at a single point lying
exactly at centre of molecule called point group .”
 All the symmetry molecule categorized into 3 types
 1.Molecules of low symmetry (MLS)
 2.Molecules of high symmetry(MHS)
 3.Molecules of special symmetry(MSS)

20. 1.Molecules of low symmetry (MLS)
I. C1 ⇒ e.g. CHFClBr
II. Cs ⇒ e.g. SOCl2 , Phenol
III. Ci ⇒ e.g. Trans-CHFCl - CHFCl

21. REFERENCES
 Principle of Physical Chemistry, Puri, Sharma,
Pathania.
 Inorganic Chemistry: Principle and Structure, Huheey
and Keiter.

22. THANK YOU
 I express my sincere thanks to all
my professors, seniors and my
parents.