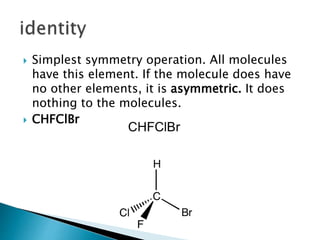
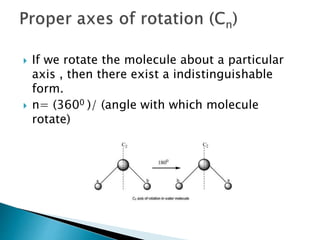
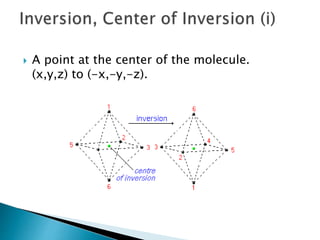
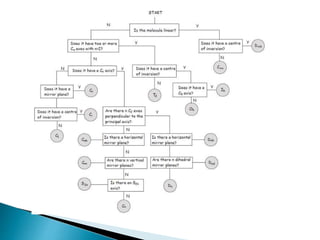
This document discusses symmetry operations and elements in molecules. It defines symmetry operations as actions that leave an object looking the same, and symmetry elements as the axes, planes, lines, or points with respect to which symmetry operations are carried out. It provides examples of common symmetry elements like identity, planes of reflection, inversion centers, proper and improper rotation axes. The document analyzes the symmetry of a specific molecule and determines it has D3h point group symmetry based on possessing a C3 axis, 3 C2 axes, and a horizontal plane of symmetry.

1. SUBMITTED TO: Dr. (Mrs.) Beena Bhatia
SUBMITTED BY: Vishal Kumar Jangid
M.Sc Final (Physics)-2017

2.  Symmetry operation: is an action that leaves
an object looking the same after it has been
carried out.
 Symmetry Elements: Each symmetry
operation has a corresponding symmetry
elements which is the axis, plane line or point
with respect to which the symmetry operation
is carried out.

3. Table of Elements and Operations
Element Operation Symbol
Identity Identity E
Symmetry plane
Reflection in the
plane
σ
Inversion center
Inversion of a point
x,y,z to -x,-y,-z
i
Proper axis
Rotation by
(360/n)
o
Cn
Improper axis
1. Rotation by
(360/n)
o
2. Reflection in
plane perpendicular
torotation axis
Sn

4.  Simplest symmetry operation. All molecules
have this element. If the molecule does have
no other elements, it is asymmetric. It does
nothing to the molecules.
 CHFClBr

5.  If we rotate the molecule about a particular
axis , then there exist a indistinguishable
form.
 n= (3600 )/ (angle with which molecule
rotate)

6.  A point at the center of the molecule.
(x,y,z) to (-x,-y,-z).

7.  Molecules contain mirror planes.
 σh(horizontal): plane perpendicular to
principal axis
 σd(dihedral), σv(vertical): plane linear with
principal axis
◦ σd: σ parallel to Cn and bisecting two C2' axes
◦ σv: Vertical, parallel to principal axis

8.  This is a compound operation combining a
rotation (Cn) with a reflection through a plane
perpendicular to the Cn axis σh.(Cn followed
by σh)
 σCn=Sn

9.  It is only possible for certain combinations of
symmetry elements to be present in a
molecule .
 we may group together molecules that
possess the same symmetry elements and
classify molecules according to their
symmetry.
 These groups of symmetry elements are
called point groups

11.  linear low symmetry? No
 Cn axis? Yes- Principal axis C3 passing
through B.
 nC2 axes? Yes 3C2 axes
 σh? Yes
D3h