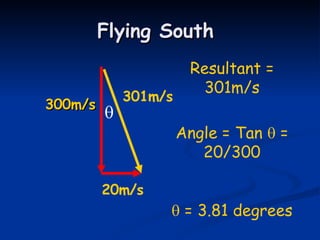
1) The document discusses how relative velocity affects the movement of objects when they encounter wind or other forces. It uses the example of an airplane flying south at 300m/s encountering a 20m/s westerly wind. 2) Using vector addition, it calculates that the resultant velocity will be 301m/s at an angle of 3.81 degrees south of due south. 3) It then considers how to determine the direction the plane must fly to still travel south at 300m/s with the same 20m/s westerly wind, calculating it needs a heading of 183.2 degrees.

1. Relative Velocity Do objects always go where you think that they will? http://www.metacafe.com/watch/39256/crosswinds/

2. Relative Velocity When we consider velocity, it is a vector. So has both magnitude and direction. When 2 things are moving with a velocity they may affect one or both of the objects On lined paper, draw the velocity vector for a plane moving South at 300m/s

3. Compass Headings

4. Flying South 300m/s But alas, there is a westerly wind of 20m/s. What effect will it have on your journey? 20m/s

5. Flying South 300m/s There will be a RESULTANT VELOCITY due to the 2 vectors Calculate its magnitude and heading 20m/s

6. Flying South 300m/s Resultant = 301m/s Angle = Tan  = 20/300  = 3.81 degrees 20m/s  301m/s

7. Flying in a pre-determined direction What if you want to fly South but the wind is the same, 20m/s from the West? Which way should you head? Required Direction (resultant) Wind 20m/s

8. Vector Addition Sin  = V air / V plane = 20 /300  = 3.82 Resultant v = √300 2 – 20 2 = 299m/s Velocity of plane is 300m/s at 183.2 heading Wind 20m/s 299 m/s resultant Velocity

9. Rules of Vector Addition Vectors are drawn with a magnitude and direction – usually as headings for velocity. E.g. North Additional vectors are added to the end of the first and drawn in the same direction if they are going in the same direction (relative to the first) Additional vectors are subtracted from the end of the first and drawn in the opposite direction if they are going in the opposite direction (relative to the first) Other vectors that are not parallel can be put end to end to work out either resultant or required velocities