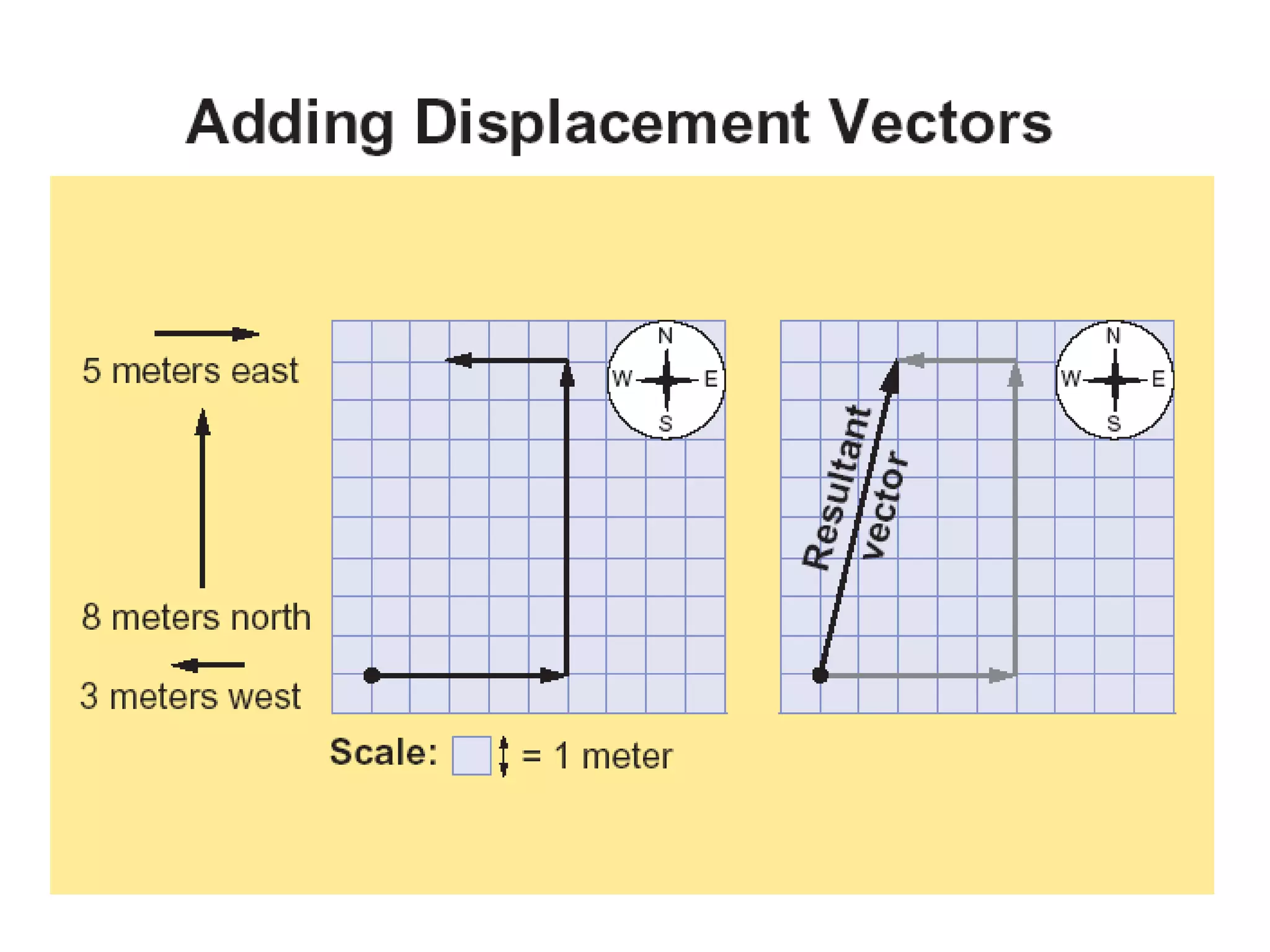
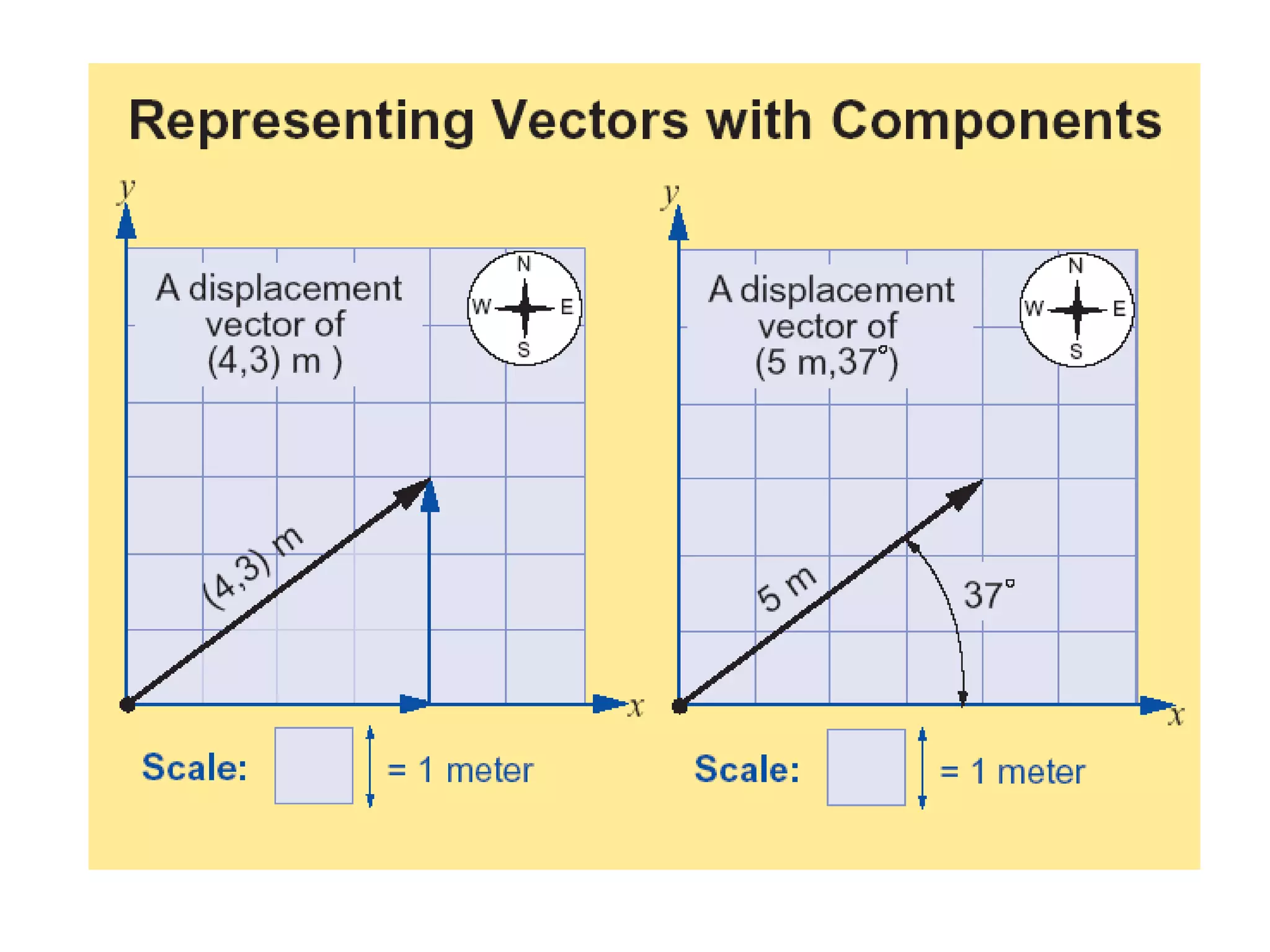
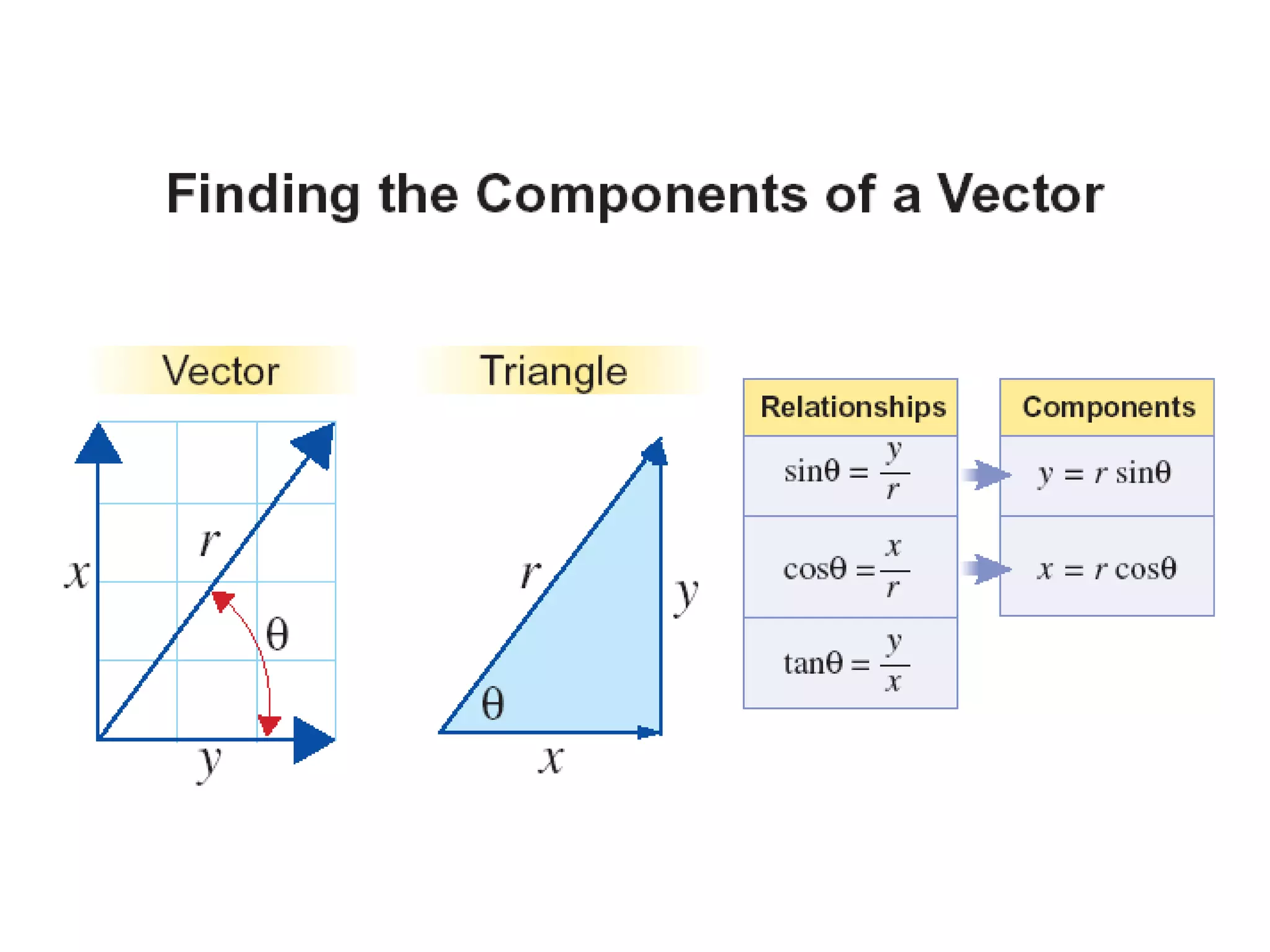
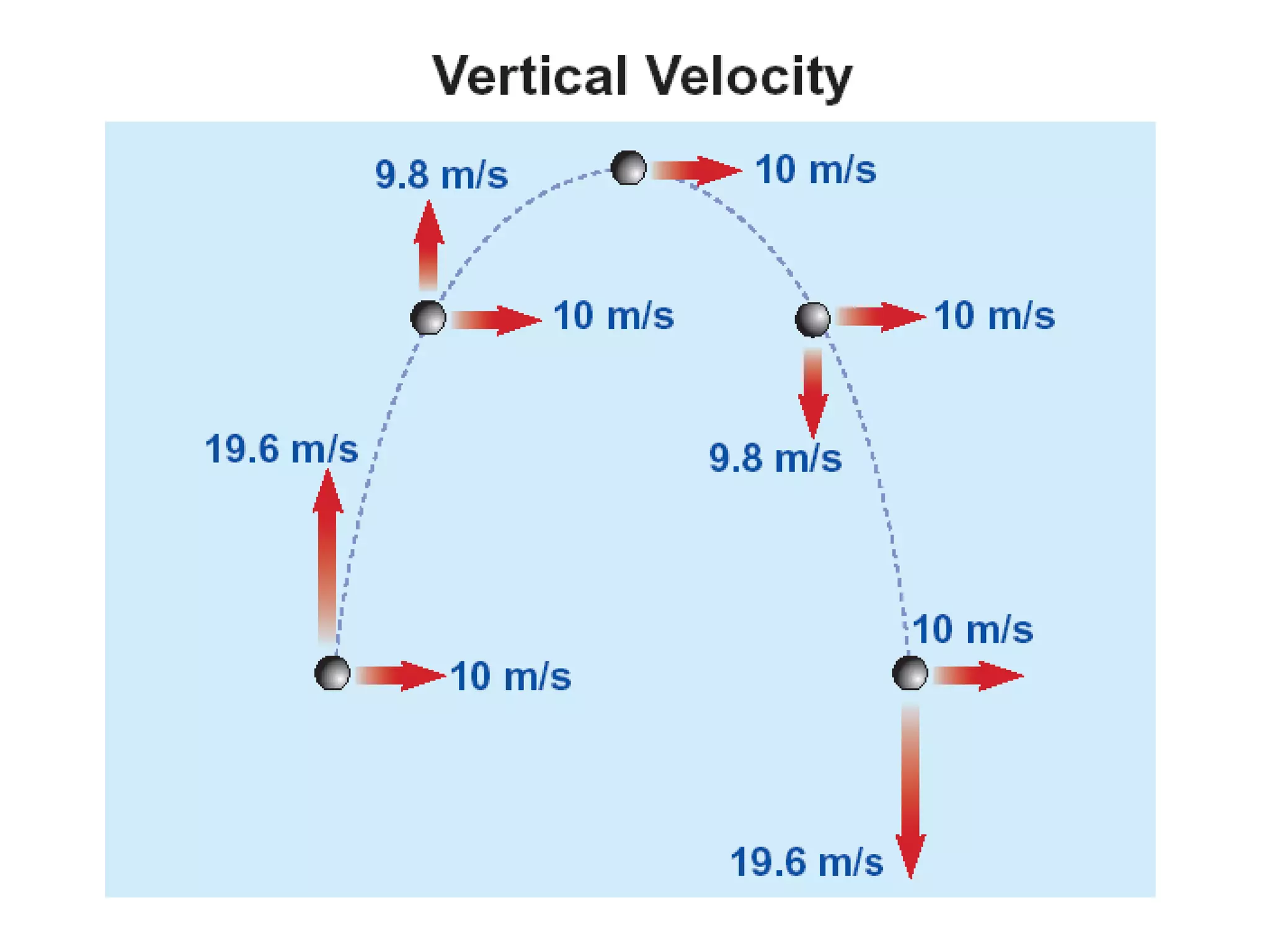
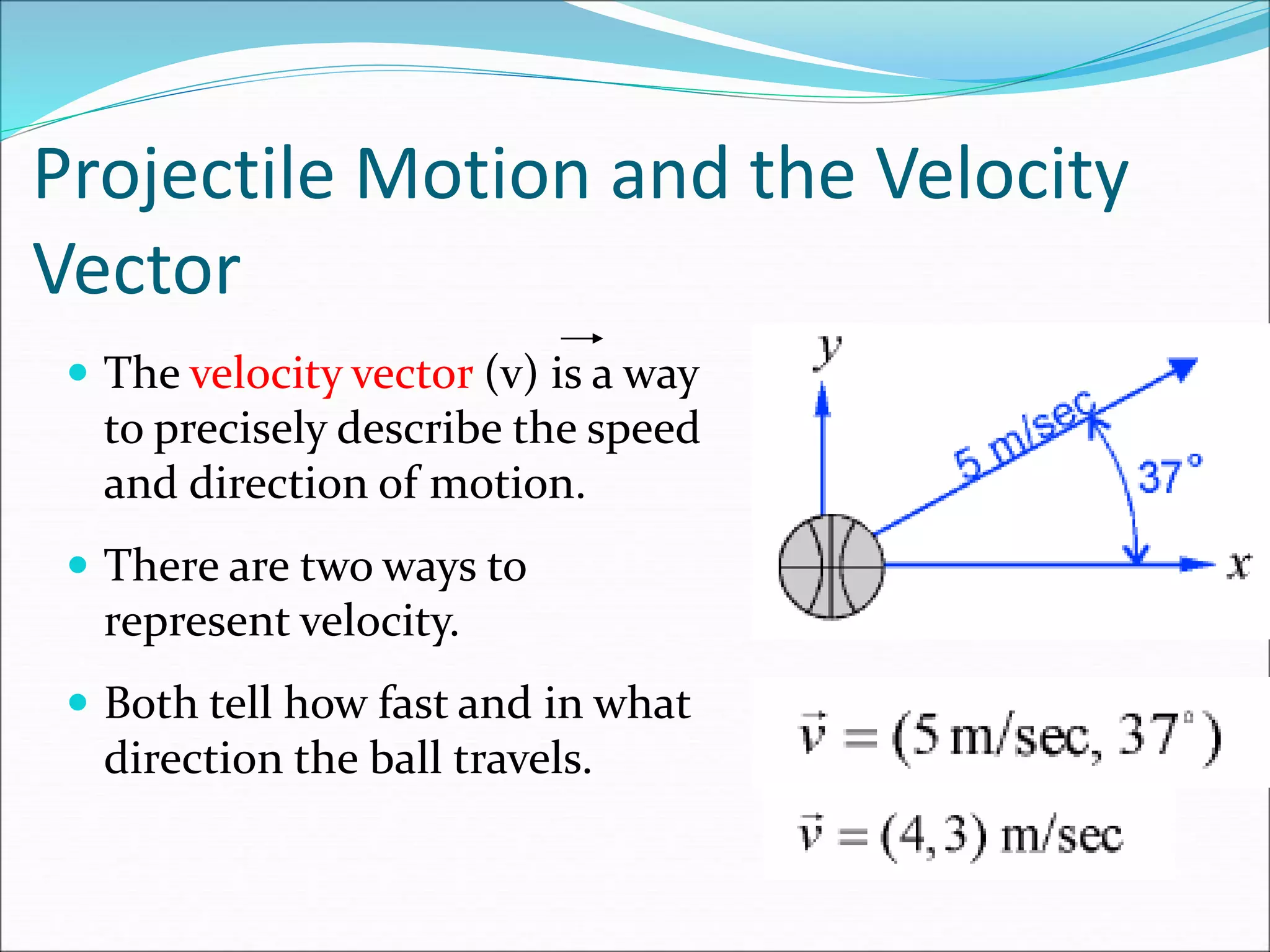
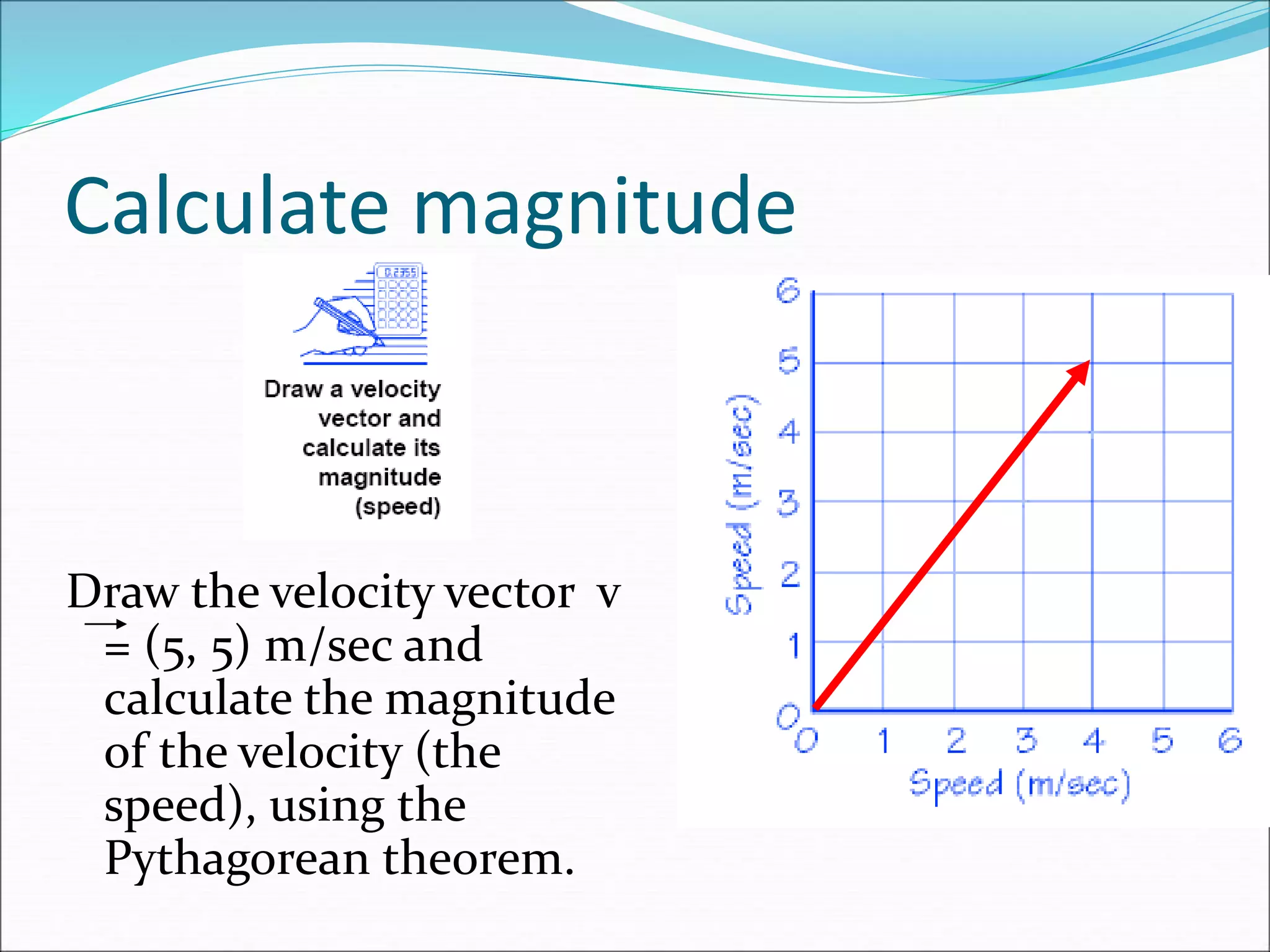
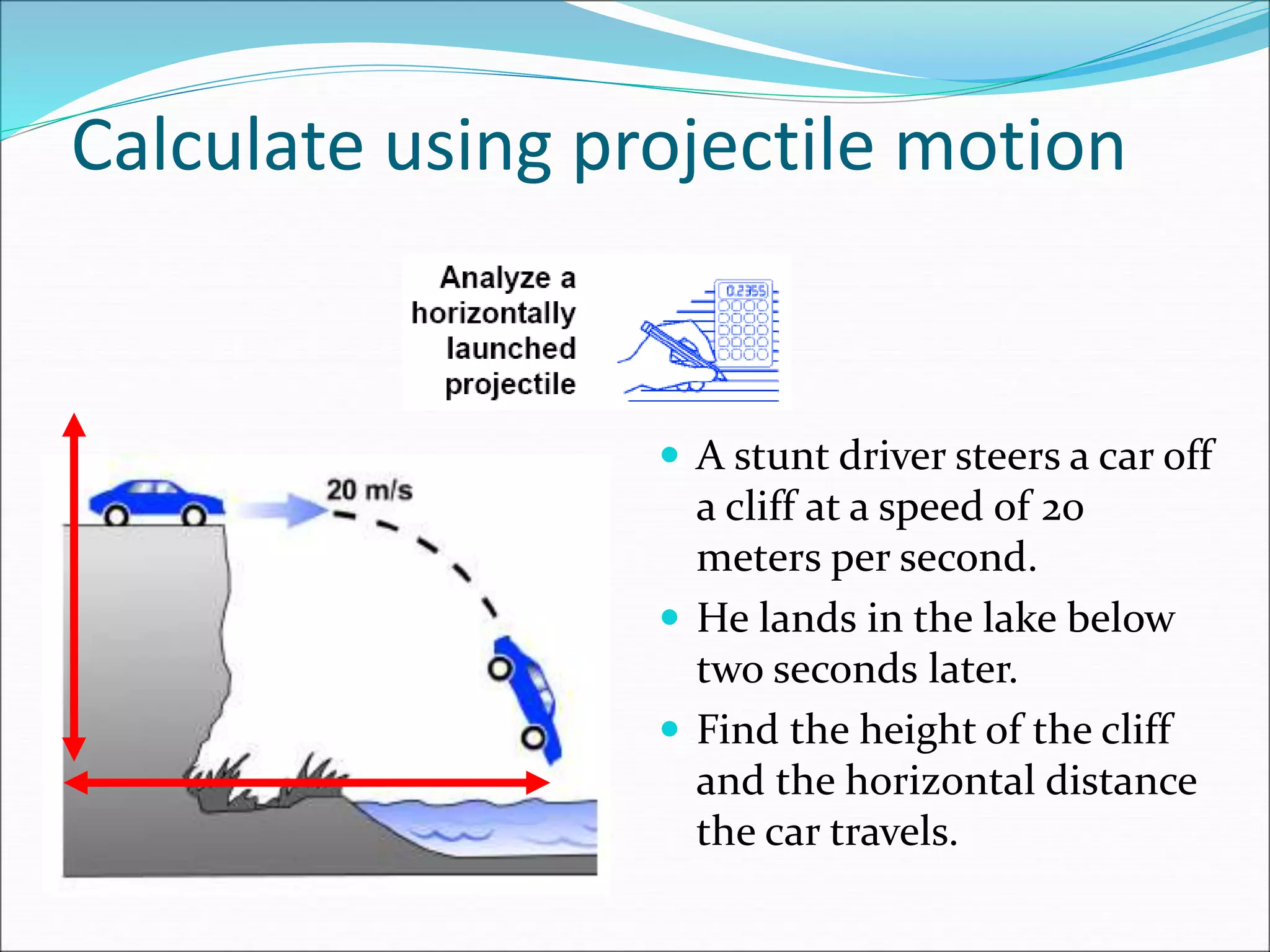
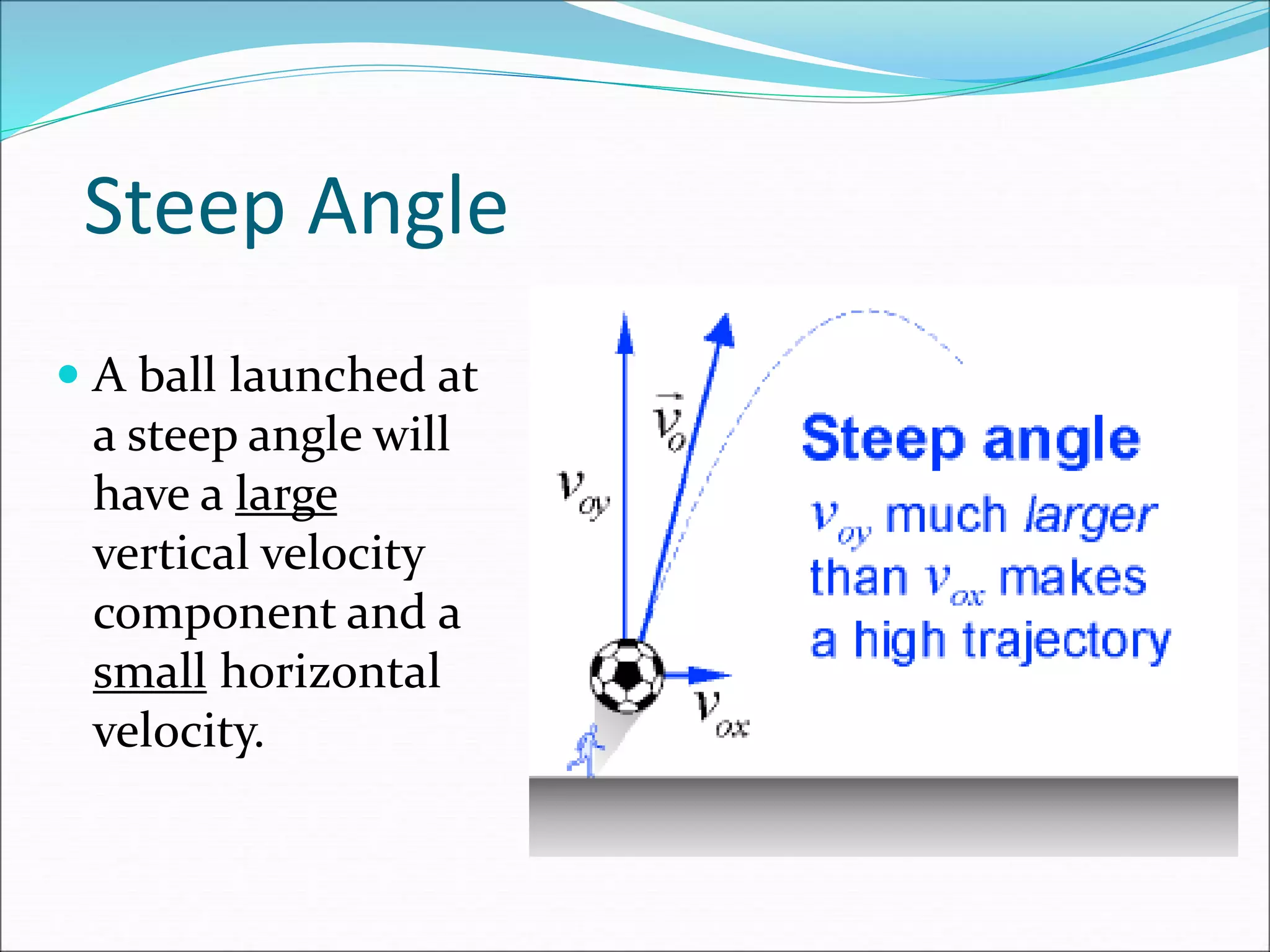
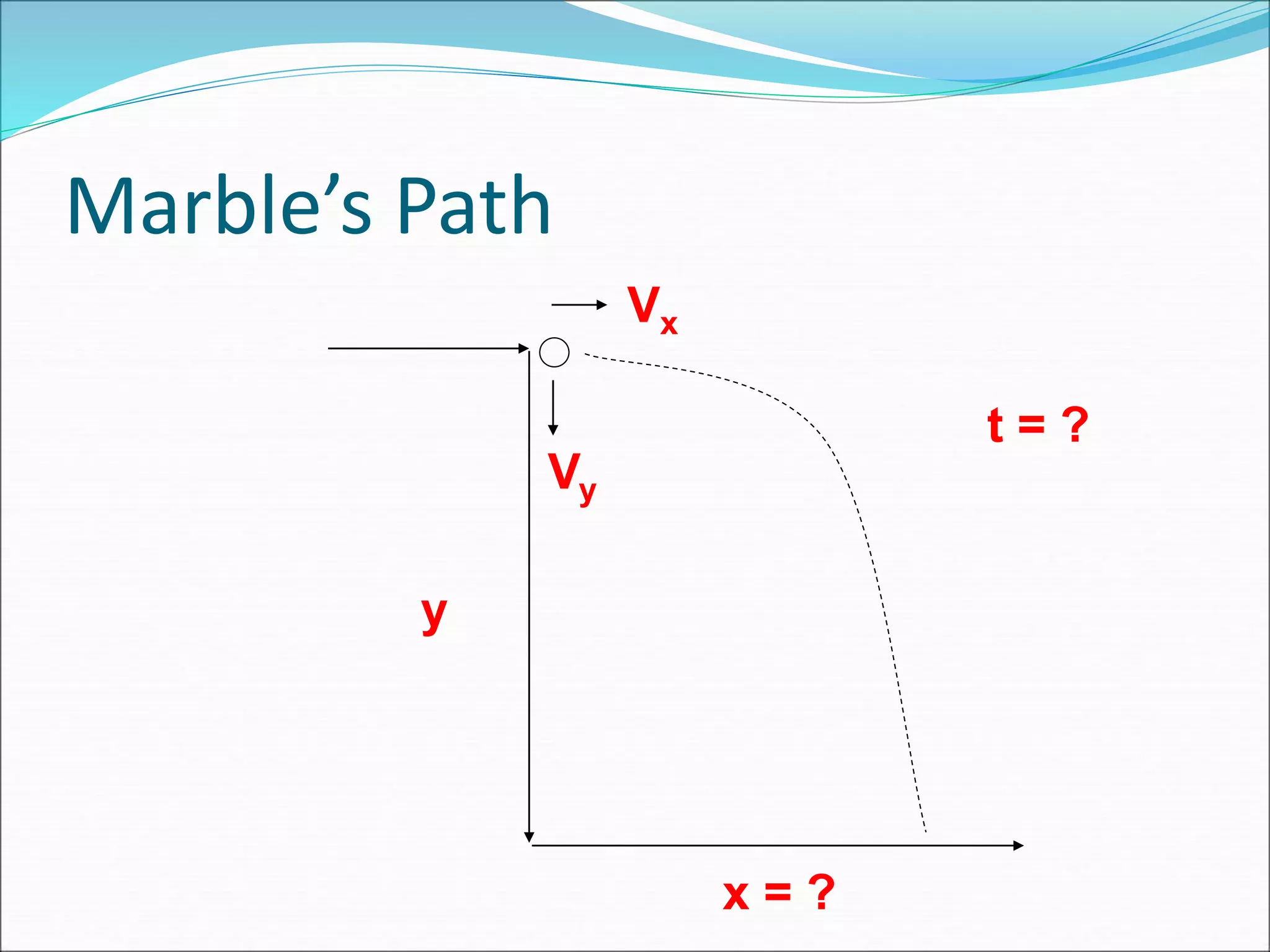
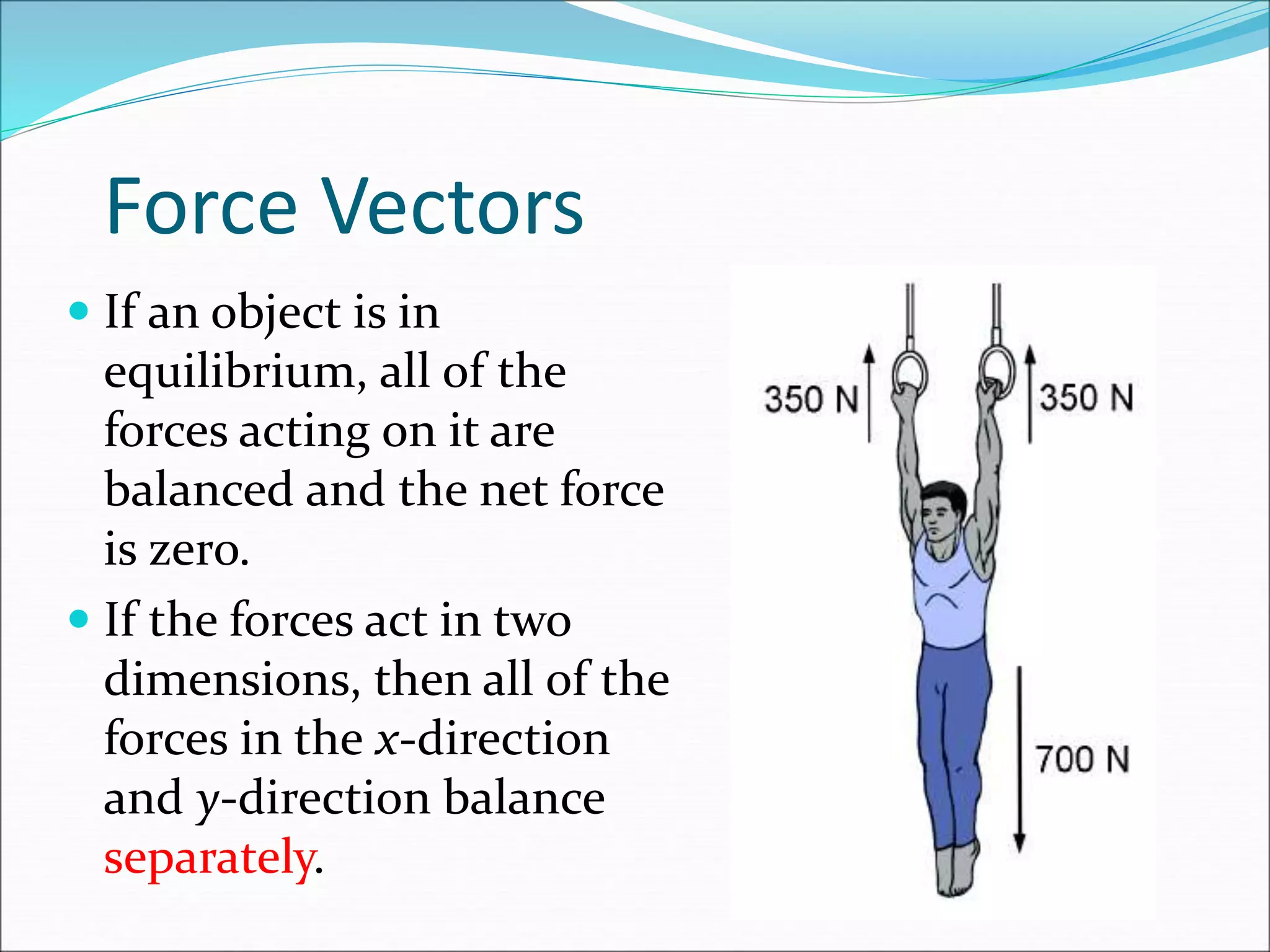
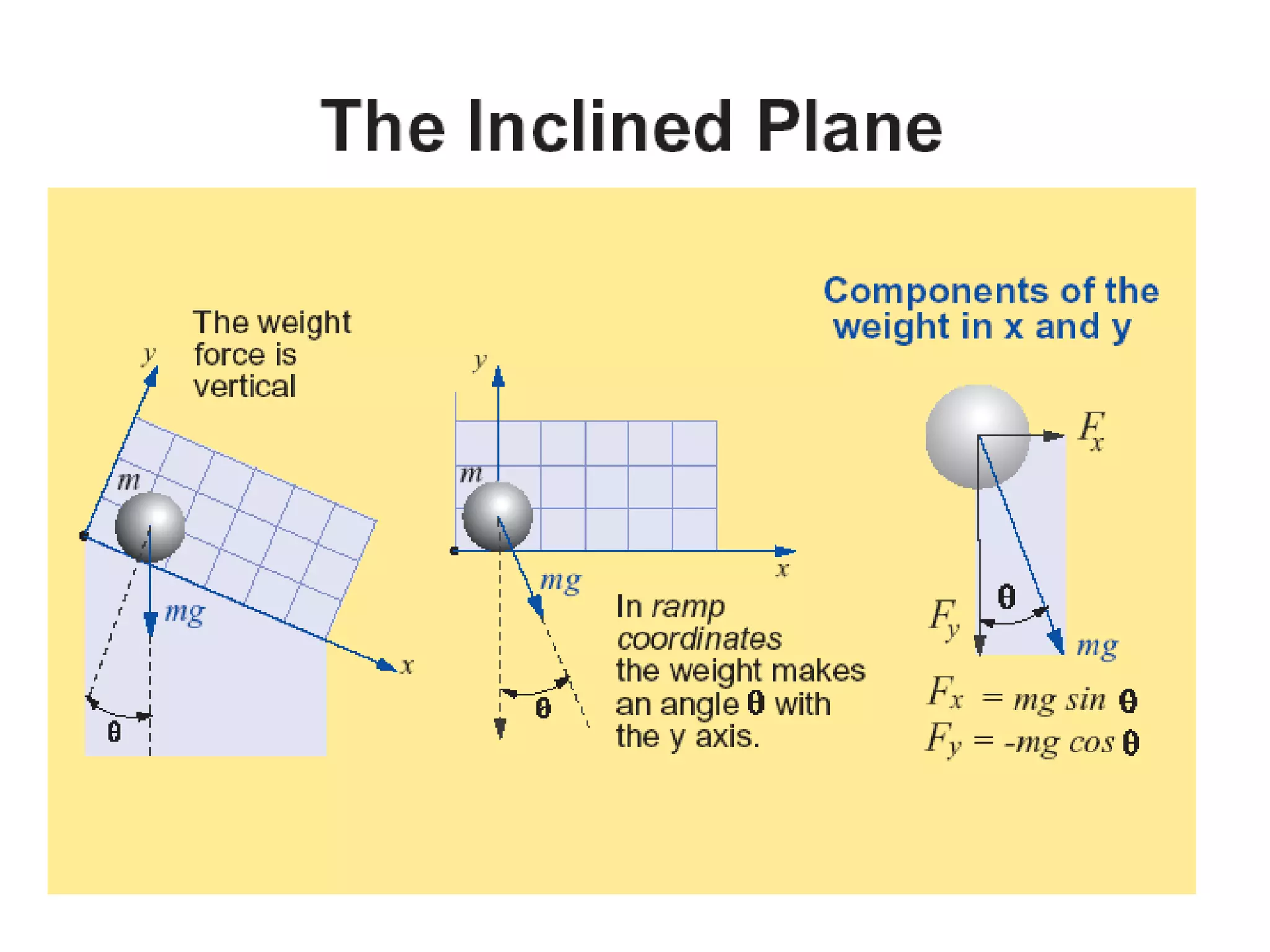
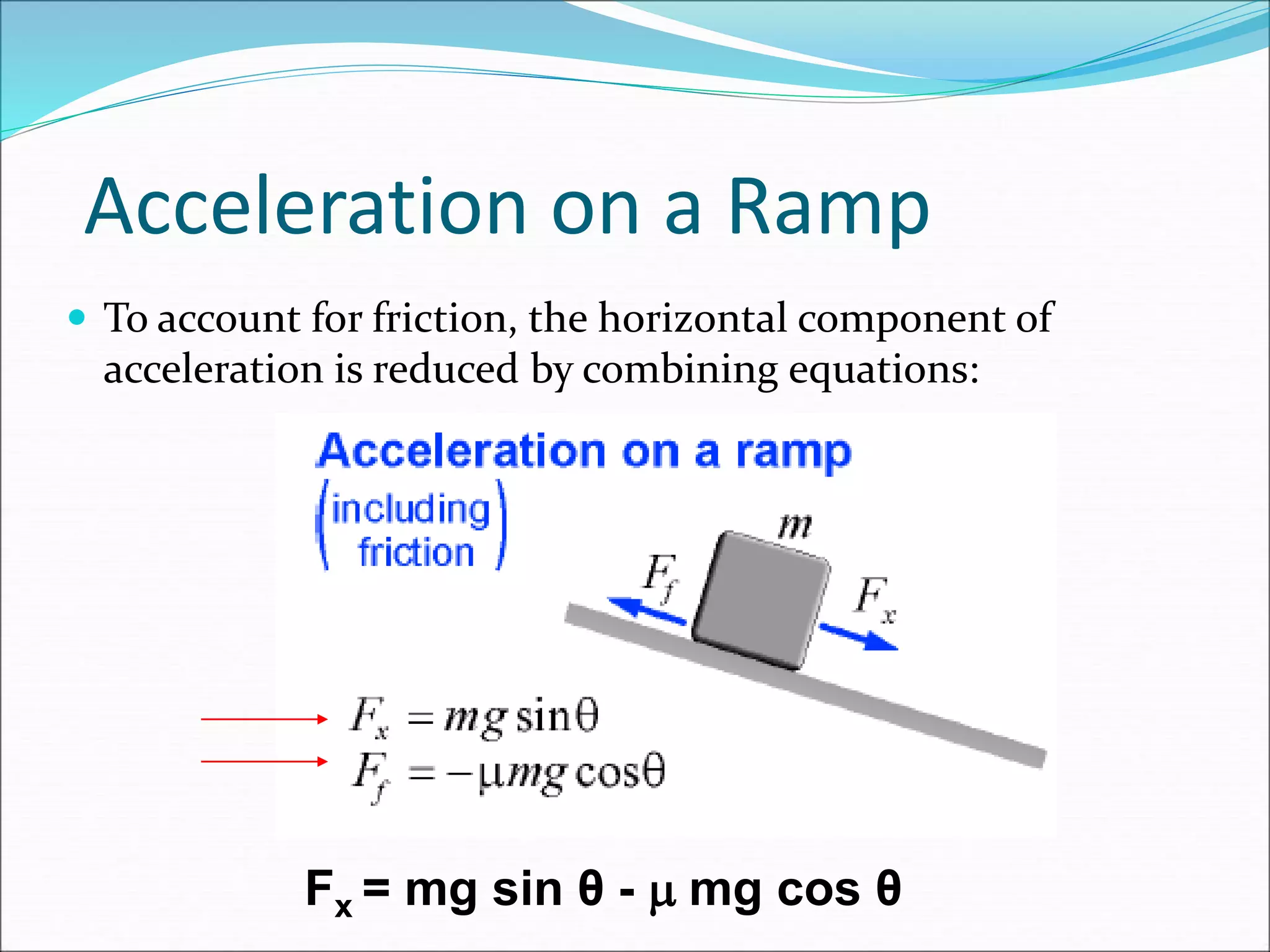
The document discusses vector concepts like displacement, velocity, and force and how to calculate their components in x and y directions. It also explains how to use vector addition and subtraction to solve problems involving projectile motion and forces in two dimensions, including calculating the acceleration on an inclined plane when given the angle of incline. The objectives cover topics like adding and subtracting vectors, writing vectors in polar and x-y coordinates, and using force vectors to solve two-dimensional equilibrium problems.

1. Vector Objectives
1. Add and subtract displacement vectors to describe
changes in position.
2. Calculate the x and y components of a displacement,
velocity, and force vector.
3. Write a velocity vector in polar and x-y coordinates.
4. Calculate the range of a projectile given the initial velocity
vector.
5. Use force vectors to solve two-dimensional equilibrium
problems with up to three forces.
6. Calculate the acceleration on an inclined plane when
given the angle of incline.

2. Chapter 7 Vocabulary Terms
 vector
 scalar
 magnitude
 x-component
 y-component
 cosine
 parabola
 Pythagorean
theorem
 displacement
 resultant
 position
 resolution
 right triangle
 sine
 dynamics
 tangent
 normal force
 projectile
 trajectory
 Cartesian
coordinates
 range
 velocity vector
 equilibrium
 inclined plane
 polar coordinates
 scale component

3. 7.1 Vectors and Direction
Key Question:
How do we accurately
communicate length
and distance?
*Students read Section 7.1 AFTER Investigation 7.1

4. Vectors and Direction
 A scalar is a quantity that
can be completely
described by one value: the
magnitude.
 You can think of magnitude
as size or amount,
including units.

5. Vectors and Direction
 A vector is a quantity that
includes both magnitude
and direction.
 Vectors require more than
one number.
 The information “1
kilometer, 40 degrees east
of north” is an example of a
vector.

6. Vectors and Direction
 In drawing a vector as an
arrow you must choose a
scale.
 If you walk five meters
east, your displacement
can be represented by a 5
cm arrow pointing to the
east.

7. Vectors and Direction
 Suppose you walk 5 meters east,
turn, go 8 meters north, then
turn and go 3 meters west.
 Your position is now 8 meters
north and 2 meters east of
where you started.
 The diagonal vector that
connects the starting position
with the final position is called
the resultant.

8. Vectors and Direction
 The resultant is the sum of two
or more vectors added together.
 You could have walked a shorter
distance by going 2 m east and
8 m north, and still ended up in
the same place.
 The resultant shows the most
direct line between the starting
position and the final position.

11. Calculate a resultant vector
 An ant walks 2 meters West, 3 meters North,
and 6 meters East.
 What is the displacement of the ant?

12. Finding Vector Components
Graphically
 Draw a
displacement
vector as an arrow
of appropriate
length at the
specified angle.
 Mark the angle and
use a ruler to draw
the arrow.

14. Finding the Magnitude of a Vector
 When you know the x- and y- components of a vector, and
the vectors form a right triangle, you can find the
magnitude using the Pythagorean theorem.

15. 7.1 Adding Vectors
 Writing vectors in components make it easy to add them.

16. Subtracting Vectors

17. Calculate vector magnitude
 A mail-delivery robot
needs to get from where it
is to the mail bin on the
map.
 Find a sequence of two
displacement vectors that
will allow the robot to
avoid hitting the desk in
the middle.

18. Projectile Motion and the Velocity
Vector
 Any object that is
moving through the air
affected only by gravity
is called a projectile.
 The path a projectile
follows is called its
trajectory.

19. Projectile Motion and the Velocity
Vector
 The trajectory of a
thrown basketball
follows a special type of
arch-shaped curve called
a parabola.
 The distance a projectile
travels horizontally is
called its range.

21. Projectile Motion and the Velocity
Vector
 The velocity vector (v) is a way
to precisely describe the speed
and direction of motion.
 There are two ways to
represent velocity.
 Both tell how fast and in what
direction the ball travels.

22. Calculate magnitude
Draw the velocity vector v
= (5, 5) m/sec and
calculate the magnitude
of the velocity (the
speed), using the
Pythagorean theorem.

23. Components of the Velocity Vector
 Suppose a car is driving 20
meters per second.
 The direction of the vector
is 127 degrees.
 The polar representation
of the velocity is v = (20
m/sec, 127°).

24. Calculate velocity
 A soccer ball is kicked at a speed of 10 m/s and an angle
of 30 degrees.
 Find the horizontal and vertical components of the ball’s
initial velocity.

25. Adding Velocity Components
 Sometimes the total velocity of an object is a combination of
velocities.
 One example is the motion of a boat on a river.
 The boat moves with a certain velocity relative to the
water.
 The water is also moving with another velocity relative to
the land.

26. Adding Velocity Components

27. Calculate velocity components
 An airplane is moving at a velocity of 100 m/s in a direction 30
degrees NE relative to the air.
 The wind is blowing 40 m/s in a direction 45 degrees SE relative
to the ground.
 Find the resultant velocity of the airplane relative to the
ground.

28. Projectile Motion
 When we drop a ball
from a height we know
that its speed increases
as it falls.
 The increase in speed is
due to the acceleration
gravity, g = 9.8 m/sec2.
Vx
Vy
x
y

29. Horizontal Speed
 The ball’s horizontal velocity
remains constant while it
falls because gravity does not
exert any horizontal force.
 Since there is no force, the
horizontal acceleration is
zero (ax = 0).
 The ball will keep moving to
the right at 5 m/sec.

30. Horizontal Speed
 The horizontal distance a projectile moves can be
calculated according to the formula:

31. Vertical Speed
 The vertical speed (vy) of the
ball will increase by 9.8 m/sec
after each second.
 After one second has passed,
vy of the ball will be 9.8 m/sec.
 After the 2nd second has
passed, vy will be 19.6 m/sec
and so on.

33. Calculate using projectile motion
 A stunt driver steers a car off
a cliff at a speed of 20
meters per second.
 He lands in the lake below
two seconds later.
 Find the height of the cliff
and the horizontal distance
the car travels.

34. Projectiles Launched at an Angle
 A soccer ball kicked
off the ground is
also a projectile, but
it starts with an
initial velocity that
has both vertical and
horizontal
components.
*The launch angle determines how the initial velocity
divides between vertical (y) and horizontal (x) directions.

35. Steep Angle
 A ball launched at
a steep angle will
have a large
vertical velocity
component and a
small horizontal
velocity.

36. Shallow Angle
 A ball launched at
a low angle will
have a large
horizontal velocity
component and a
small vertical one.

37. Projectiles Launched at an Angle
The initial velocity components of an object launched at a velocity vo
and angle θ are found by breaking the velocity into x and y
components.

38. Range of a Projectile
 The range, or horizontal distance, traveled by a
projectile depends on the launch speed and the launch
angle.

39. Range of a Projectile
 The range of a projectile is calculated from the
horizontal velocity and the time of flight.

40. Range of a Projectile
 A projectile travels farthest when launched at 45
degrees.

41. Range of a Projectile
 The vertical velocity is responsible for giving the
projectile its "hang" time.

42. "Hang Time"
 You can easily calculate your own hang time.
 Run toward a doorway and jump as high as you can, touching the wall or door frame.
 Have someone watch to see exactly how high you reach.
 Measure this distance with a meter stick.
 The vertical distance formula can be rearranged to solve for time:

43. Projectile Motion and the Velocity
Vector
Key Question:
Can you predict the landing spot of a projectile?
*Students read Section 7.2 BEFORE Investigation 7.2

44. Marble’s Path
Vy
x = ?
y
Vx
t = ?

45. In order to solve “x” we must know
“t”
Y = vot – ½ g t2
2y = g t2
vot = 0 (zero)
Y = ½ g t2
t2 = 2y
g
t = 2y
g

46. Forces in Two Dimensions
 Force is also represented in x-y components.

47. Force Vectors
 If an object is in
equilibrium, all of the
forces acting on it are
balanced and the net force
is zero.
 If the forces act in two
dimensions, then all of the
forces in the x-direction
and y-direction balance
separately.

48. Equilibrium and Forces
 It is much more difficult
for a gymnast to hold his
arms out at a 45-degree
angle.
 To see why, consider that
each arm must still
support 350 newtons
vertically to balance the
force of gravity.

49. Forces in Two Dimensions
 Use the y-component to find the total force in the
gymnast’s left arm.

50. Forces in Two Dimensions
 The force in the right arm must also be 495 newtons
because it also has a vertical component of 350 N.

51. Forces in Two Dimensions
 When the gymnast’s arms
are at an angle, only part of
the force from each arm is
vertical.
 The total force must be
larger because the vertical
component of force in each
arm must still equal half his
weight.

52. Forces and Inclined Planes
 An inclined plane is a straight surface, usually with
a slope.
 Consider a block sliding
down a ramp.
 There are three forces that
act on the block:
 gravity (weight).
 friction
 the reaction force
acting on the block.

53. Forces and Inclined Planes
 When discussing forces, the word “normal” means
“perpendicular to.”
 The normal force acting
on the block is the
reaction force from the
weight of the block
pressing against the
ramp.

54. Forces and Inclined Planes
 The normal force on
the block is equal
and opposite to the
component of the
block’s weight
perpendicular to the
ramp (Fy).

55. Forces and Inclined Planes
 The force parallel to
the surface (Fx) is
given by
Fx = mg sinθ.

57. Acceleration on a Ramp
 Newton’s second law can be used to calculate the
acceleration once you know the components of all the
forces on an incline.
 According to the second law:
a = F
m
Force (kg . m/sec2)
Mass (kg)
Acceleration
(m/sec2)

58. Acceleration on a Ramp
 Since the block can only accelerate along the ramp, the force that
matters is the net force in the x direction, parallel to the ramp.
 If we ignore friction, and substitute Newtons' 2nd Law, the net
force is:
Fx =
a =
m sin θ
g
F
m

59. Acceleration on a Ramp
 To account for friction, the horizontal component of
acceleration is reduced by combining equations:
Fx = mg sin θ - m mg cos θ

60. Acceleration on a Ramp
 For a smooth surface, the coefficient of friction (μ) is
usually in the range 0.1 - 0.3.
 The resulting equation for acceleration is:

61. Calculate acceleration on a ramp
 A skier with a mass of 50 kg is on a hill making an angle of
20 degrees.
 The friction force is 30 N.
 What is the skier’s acceleration?

62. Vectors and Direction
Key Question:
How do forces balance
in two dimensions?