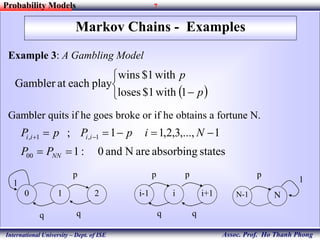
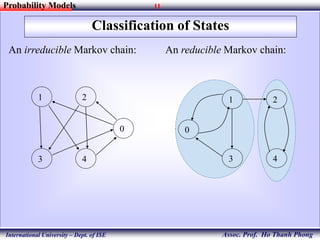
The document discusses various concepts related to stochastic processes and Markov chains, including their definitions, classifications of states, and transition probabilities. It presents examples such as weather forecasting and gambling models to illustrate these concepts. The document also covers important equations and properties like Chapman-Kolmogorov equations, recurrence vs. transience, and limiting probabilities.