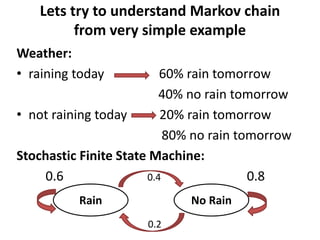
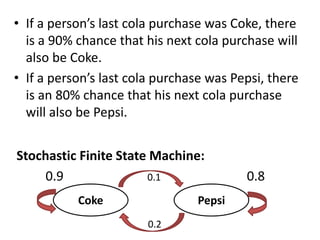
This document presents a summary of the Markov chain model. It begins with an introduction to development planning models and an overview of the Markov chain model and its properties. It then discusses the origin of Markov chains and how they were introduced by Andrey Markov. Several applications of Markov chain models are provided, such as market research, text generation, and customer journey predictions. Finally, the document concludes with a simple example of using a Markov chain to model weather patterns.

1. A Presentation on
Markov Chain Model
Course Title: Development Planning and Management
Course Code: DS 3109
Presented to-
Asma Ul Husna
Assistant Professor
Development Studies Discipline
Khulna University
Presented by-
Md. Ayatullah Khan
Student ID: 152119
Development Studies Discipline
Khulna University
Date of Submission: 29 October, 2017

2. Table of Content
• Introduction
• Origin of Markov Chain Model
• What is Markov Chain Model?
• Markov assumptions
• Configuration of the Markov-Chain Model
• Markov Chain Application
• Example of Markov Chain Model
• Conclusion

3. Introduction
• Development planning contains a number of
theories and planning models. Markov model is
one of the best planning model of them.
• Markov model is a stochastic model used to
model randomly changing systems where it is
assumed that future states depend only on the
current state not on the events that occurred
before it (that is, it assumes the Markov
property).

4. • Markov chain model is one of the most
powerful tools for analyzing complex
stochastic system.
• Markov chain model have become popular
in manpower planning system. Several
researchers have adopted Markov chain
models to clarify manpower policy issues.

5. Origin of Markov Chain Model
• Markov chains were introduced in 1906 by Andrey Markov
(1856–1922)and were named in his honor.
• Andrey Markov studied Markov chains in the early 20th
century.
• Markov was interested in studying an extension of
independent random sequences, motivated by a
disagreement with Pavel Nekrasov .
• In his first paper on Markov chains, Markov showed that
under certain conditions the average outcomes of the
Markov chain would converge to a fixed vector of values.
• Markov later used Markov chains to study the distribution
of vowels in Eugene Onegin, written by Alexander Pushkin,
and proved a central limit theorem for such chains.

6. • Markov-Chain(Markov 1914) has been applied
to short term market forecasting and business
decision, on the future market the firms'
future market share, given a consumer
transition from one firm to the next.

7. What is Markov Chain Model?
• A stochastic model that describe the probabilities
of transition among the states of a system.
• It is a random process that undergoes transitions
from one state to another on a state space.
• Change of states depends probabilistically only on
the current state of the system.
• It is required to possess a property that is usually
characterized as "memoryless": the probability
distribution of the next state depends only on the
current state and not on the sequence of events
that preceded it.

8. • a Markov chain model is defined by a set of
states
some states emit symbols
other states (e.g. the begin state) are silent
• Changes of state depends probabilistically on
the current state of the system.
• Markov chain model makes calculation of
conditional probability easy.

9. Markov assumptions
• The probabilities of moving from a state to all
others sum to one.
• The probabilities apply to all system
participants.
• The probabilities are constant over time.

10. Configuration of the Markov-Chain
Model
• Markov systems deal with stochastic environments
in which possible "outcomes occur at the end of a
well-defined, usually first period“.
• This situation further involves a multi-period time
frame, during which the occurring consumer's
transient behavior, for example, affects the
stability of the firm's performance.
• This transient behavior, whose future outcome is
unknown but needs to be predicated, creates
inter-period transitional probabilities.

11. • Such a stochastic process, known as the
Markov process, contains a special case,
where the transitional probabilities from one
time period to another remains stationary, in
which case the process is referred to as the
Markov-Chain.

12. Markov Chain Application
Market research problems (Market share
predictions)
• Markov text generators
• Asset pricing and other financial predictions
• Customer journey predictions
• Population genetics
• Algorithmic music composition
• Page ranks (Google results)

13. Lets try to understand Markov chain
from very simple example
Weather:
• raining today 60% rain tomorrow
40% no rain tomorrow
• not raining today 20% rain tomorrow
80% no rain tomorrow
Stochastic Finite State Machine:
0.6 0.4 0.8
0.2
Rain No Rain

14. • If a person’s last cola purchase was Coke, there
is a 90% chance that his next cola purchase will
also be Coke.
• If a person’s last cola purchase was Pepsi, there
is an 80% chance that his next cola purchase
will also be Pepsi.
Stochastic Finite State Machine:
0.9 0.1 0.8
0.2
Coke Pepsi

15. Conclusion
• Markov chain is a simple concept which can
explain most complicated real time Many of
the Artificial intelligence tools use this simple
principle called Markov chain in some form.
• This presentation illustrates how easy it is to
understand this concept and some of it’s
applications.

16. Thank You