This document discusses Markov chains and related topics: - It defines Markov chains as stochastic processes that take values in a countable set, with the memoryless property that future states only depend on the present state. - It distinguishes between discrete-time and continuous-time Markov chains, and introduces transition probabilities and matrices. - It covers Chapman-Kolmogorov equations for calculating multi-step transition probabilities recursively, and the concept of a stationary distribution when state probabilities converge over time. 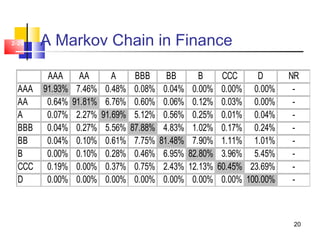- Examples discussed include transforming processes into Markov chains, a camera inventory model, and using Markov chains to model bond credit ratings. 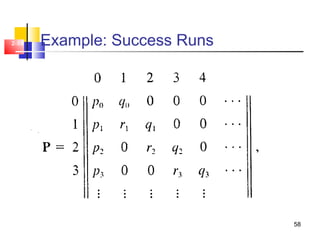- Special cases like two-state chains, independent random variables, random walks

1. 1
Bab 3 Karlin

2. 2
2-2

3. 3
2-3 Markov Chain
 Stochastic process that takes values in a countable
set
 Example: {0,1,2,…,m}, or {0,1,2,…}
 Elements represent possible “states”
 Chain “jumps” from state to state
 Memoryless (Markov) Property: Given the present
state, future jumps of the chain are independent of
past history
 Markov Chains: discrete- or continuous- time

4. 4
2-4 Discrete-Time Markov Chain
 Discrete-time stochastic process {Xn: n = 0,1,2,…}
 Takes values in {0,1,2,…}
 Memoryless property:
 Transition probabilities Pij
 Transition probability matrix P=[Pij]
1 1 1 0 0 1
1
{ | , ,..., } { | }
{ | }
n n n n n n
ij n n
P X j X i X i X i P X j X i
P P X j X i
+ − − +
+
= = = = = = =
= = =
0
0, 1ij ij
j
P P
∞
=
≥ =∑

5. 5
2-5 Chapman-Kolmogorov Equations
 n step transition probabilities
 Chapman-Kolmogorov equations
is element (i, j) in matrix Pn
Recursive computation of state probabilities
{ | }, , 0, , 0n
ij n m mP P X j X i n m i j+= = = ≥ ≥
n
ijP
0
, , 0, , 0n m n m
ij ik kj
k
P P P n m i j
∞
+
=
= ≥ ≥∑
0 1, if
0, if
ij
i j
P
i j
=
= 
≠

6. 6
2-6 Proof of Chapman-Kolmogorov

7. 7
2-7 State Probabilities – Stationary Distribution
 State probabilities (time-dependent)
 In matrix form:
 If time-dependent distribution converges to a limit
 π is called the stationary distribution
Existence depends on the structure of Markov chain
1
1 1
0 0
{ } { } { | }π πn n
n n n n j i ij
i i
P X j P X i P X j X i P
∞ ∞
−
− −
= =
= = = = = ⇒ =∑ ∑
0 1π { }, π (π ,π ,...)n n n n
j nP X j= = =
1 2 2 0
π π π ... πn n n n
P P P− −
= = = =
π lim πn
n→∞
=
π πP=

8. Example: Transforming a Process
into a Markov Chain
2-8

9. 9
2-9

10. 10
2-10

11. 11
Example: Camera Inventory

12. 12
2-12
monday

13. 13
2-13

14. 14
2-14

15. 15
2-15

16. 16
2-16

17. 17
2-17

18. 18
2-18

19. 19
2-19

20. 20
2-20 A Markov Chain in Finance
AAA AA A BBB BB B CCC D NR
AAA 91.93% 7.46% 0.48% 0.08% 0.04% 0.00% 0.00% 0.00% -
AA 0.64% 91.81% 6.76% 0.60% 0.06% 0.12% 0.03% 0.00% -
A 0.07% 2.27% 91.69% 5.12% 0.56% 0.25% 0.01% 0.04% -
BBB 0.04% 0.27% 5.56% 87.88% 4.83% 1.02% 0.17% 0.24% -
BB 0.04% 0.10% 0.61% 7.75% 81.48% 7.90% 1.11% 1.01% -
B 0.00% 0.10% 0.28% 0.46% 6.95% 82.80% 3.96% 5.45% -
CCC 0.19% 0.00% 0.37% 0.75% 2.43% 12.13% 60.45% 23.69% -
D 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 100.00% -

21. 21
First Step Analysis

22. 22
2-22

23. 23
2-23 Simple FSA

24. 24
2-24

25. 25
2-25

26. 26
2-26

27. 27
2-27

28. 28
2-28

29. 29
2-29 FSA- Extension

30. 30
2-30

31. 31
2-31

32. 32
2-32 Example - 1
What is 1 1 1 1, , , and ?u u v v
See pg 120

33. 33
2-33

34. 34
2-34

35. 35
2-35 Example - 2
Fecundity Model
 The states are
 E0: prepuberty
 E1: Single
 E2: Married
 E3: Divorced
 E4: Widowed
 E5: Δ

36. 36
2-36

37. 37
2-37

38. 38
2-38

39. 39
Special MC

40. 40
2-40 1. Two-State MC

41. 41
2-41

42. 42
2-42

43. 43
2-43

44. 44
2-44 Numerical Example

45. 45
2-45 Another Special MC
 Independent Random Variables
 Successive Maxima
 Partial Sums
 One-Dimensional Random Walks (Player fortune)
 Success Runs

46. 46
2-46 Independent Random Variables

47. 47
2-47 Successive Maxima

48. 48
2-48

49. 49
2-49 One-Dimensional Random Walks

50. 50
2-50

51. 51
2-51 Example: Player Fortune

52. 52
2-52

53. 53
2-53

54. 54
2-54 Example: Another Random Walks (r=0)

55. 55
2-55

56. 56
2-56

57. 57
2-57

58. 58
2-58 Example: Success Runs

59. 59
Functionals of Random Walks and
Success Runs
Tugas Kelompok

60. 60
Another Look at First Step Analysis
Tugas Kelompok

61. 61
Branching Processes

62. 62
2-62

63. 63
2-63 Example: Electron Multipliers

64. 64
2-64 Example: Neutron Chain Reaction

65. 65
2-65 Example: Survival of Family Names

66. 66
2-66 Example Survival of Mutant Genes

67. 67
2-67 Mean and Variance of Branching Process

68. 68
2-68

69. 69
2-69

70. 70
2-70 Extinction Probabilities

71. 71
2-71

72. 72
2-72

73. 73
2-73

74. 74
Branching Processes and Generating
Functions
Tugas Kelompok