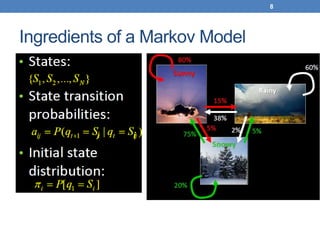
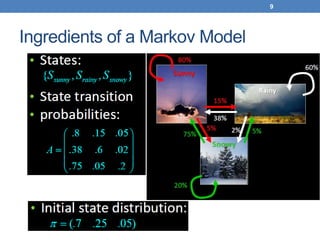
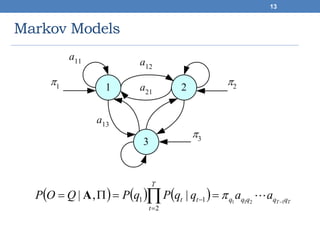
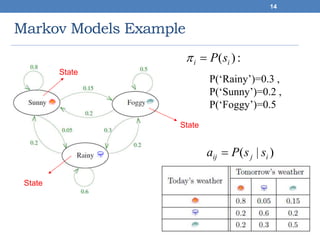
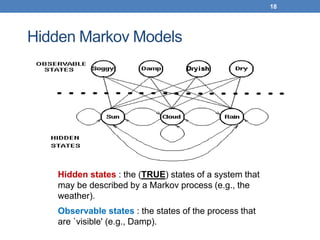
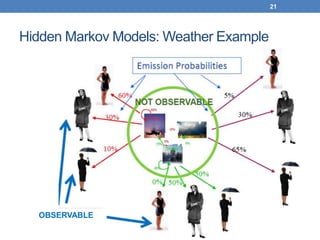
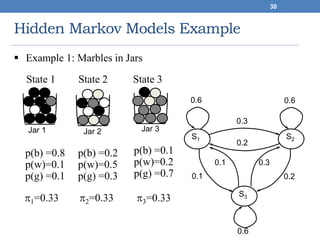
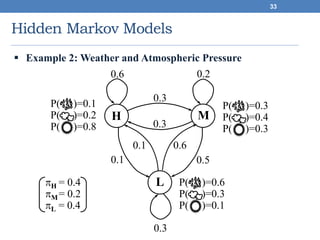
This document discusses hidden Markov models (HMMs). It begins by covering Markov chains and Markov models. It then defines HMMs, noting that they have hidden states that can produce observable outputs. The key components of an HMM - the transition probabilities, observation probabilities, and initial probabilities - are explained. Examples of HMMs for weather and marble jars are provided to illustrate calculating probabilities. The main issues in using HMMs are identified as evaluation, decoding, and learning. Evaluation calculates the probability of an observation sequence given a model. Decoding finds the most likely state sequence that produced an observation sequence. Learning determines model parameters to best fit training data.

1. BFCI
MACHINE LEARNING
CS614
Prepared by: MahmoudAhmed El-Tayeb
Supervised by: Prof. Dr. Hala HelmyZayed
1
Hidden Markov Model

2. Agenda
 Markov Chain & Markov Models
 Hidden Markov Model
 Main Issues Using HMMs:
• Evaluation
• Decoding
• Learning
2

3. Agenda
 Markov Chain & Markov Models
 Hidden Markov Model
 Main Issues Using HMMs:
• Evaluation
• Decoding
• Learning
3

4. History!!
4
Andrey Markov (1856 – 1922) was a
Russian mathematician best known for
his work on stochastic processes. A
primary subject of his research later
became known as Markov chains and
Markov processes.
Markov model is a stochastic model used to
model randomly changing systems. It is
assumed that future states depend only on the
current state, not on the events that occurred
before it (that is, it assumes the Markov
property).

5. 5
Weather:
• Raining today 40% rain tomorrow
60% no rain tomorrow
• Not raining today 20% rain tomorrow
80% no rain tomorrow
Markov Process
Simple Example







8.02.0
6.04.0
P
• Stochastic matrix:
Rows sum up to 1
The transition matrix:

6. •
6
Markov Chains Parameters
Sunny
Rain
Cloudy
2-State transition matrix : The probability of
the weather given the previous day's
weather.
3-Initial Distribution : Defining the probability of the
system being in each of the states at time 0.
1-States : Three states
- sunny, cloudy, rainy.

7. Weather: A Markov Model
• Probability of moving
to a given state
depends only on the
current state: 1st
Order Markovian
7

8. Ingredients of a Markov Model
8
j i

9. Ingredients of a Markov Model
9

10. Probability of a Time Series
• Given:
10

11. Markov chain property
 Discrete Markov System
- It is easy to depict a Markov system as a graph.
- N distinct states: S1, S2, ..., SN state at “time” t , qt = Si
- Begins (at time t=1) in some initial state(s).
- At each time step (t=1,2,…) the system moves from currentto next
state (possibly the same as the current state) according to transition
probabilitiesassociated with current state.
 Markov Property: The state of the system at time t+1 depends only
on the state of the system at time t (first order markov assumption).
11

12. Markov chain property cont.
P(qt+1=Sj | qt=Si, qt-1=Sk ,...) = P(qt+1=Sj | qt=Si)
qt=1
qt=2 qt=3 qt=4 qt=5
)()|()|()|(),,,( 11221121 iiiikikikikikii sPssPssPssPsssP  
 To define Markov model, the following probabilities have to
be specified: transition probabilities and initial
probabilities )( ii sP
12
)|( ijij ssPa 

13. Markov Models
      TT qqqqq
T
t
tt aaqqPqPQOP 1211
2
11 |,| 
 
 A
13

14. Markov Models Example
14
State
State
State
P(‘Rainy’)=0.3 ,
P(‘Sunny’)=0.2 ,
P(‘Foggy’)=0.5
:)( ii sP
)|( ijij ssPa 

15. Markov Models Example cont.
15
)sunny-foggy-sunny-rainy-rainy-foggy-sunny(P
 Suppose we want to calculate a probability of a sequence of
states in our example : ”sunny-foggy-rainy-rainy-sunny-foggy-
sunny ”
O = {“sunny-foggy -rainy-rainy-sunny- foggy -sunny”}.
Assume that S1 : sunny,
S2 : rainy,
S3 : foggy.
P(O | model)
= P(S1,S3,S2,S2,S1,S3,S1)
= P(S1).P(S3|S1).P(S2|S3). P(S2|S2). P(S1|S2).P(S3|S1).P(S1|S3)
= 𝜋1. 𝑎13 . 𝑎32. 𝑎22. 𝑎21. 𝑎13. 𝑎31
= 0.2*0.15*0.3*0.6*0.2*0.15*0.2 = 0.0000423
P(‘Rainy’)=0.3 ,
P(‘Sunny’)=0.2 ,
P(‘Foggy’)=0.5

16. Agenda
 Markov Chain & Markov Models
 Hidden Markov Model
 Main Issues Using HMMs:
• Evaluation
• Decoding
• Learning
16

17. Hidden Markov Models: Intuition
• Suppose you can’t observe the state
• You can only observe some evidence…
17

18. 18
18
Hidden Markov Models
Hidden states : the (TRUE) states of a system that
may be described by a Markov process (e.g., the
weather).
Observable states : the states of the process that
are `visible' (e.g., Damp).

19. Hidden Markov Models: Weather Example
• Observables:
19
j

20. Hidden Markov Models: Weather Example
• This means : the probability that you will see symbol k
(observing thing) given at some time t , you are in
some particular state s.
• EX: what is the probability that you will see coat (K)
, given that it is sunny (S) .
20
j

21. Hidden Markov Models: Weather Example
21
OBSERVABLE

22. Probability of a Time Series
• Given:
• What is the probability of this series?
22
Today’s
weather
Tomorrow's weather
sunny rainy snowy
sunny .8 .15 .05
rainy .38 .6 .02
snowy .75 .05 .2
weather
Observation probability
Swimming suit coat umbrella
sunny .6 0.3 .1
rainy .05 .3 .65
snowy 0 .5 .5

23. Probability of a Time Series
• Given:
23

24. Specification of an HMM
24

25. Hidden Markov Models cont.
25
 A Hidden Markov Model, is a stochastic model where the states
of the model are hidden. Each state can produce an output which
is observed.
 Each state can produce a number of outputs according to a
probability distribution, and each distinct output can potentially
be generated at any state
 Imagine: You were locked in a room for several days and you were
asked about the weather outside. The only piece of evidence you
have is whether the person who comes into the room bringing your
daily meal is carrying an umbrella or not.
o What is hidden? Sunny, Rainy, Snowy
o What can you observe? Umbrella , Coat, Swimming suit

26. Hidden Markov Models cont.
26
 To define hidden Markov model, the following probabilities
have to be specified:
- N : number of states :
- M : the number of observables:
- Matrix of transition probabilities A=(aij),
- Matrix of observation probabilities B=(bi (vm )), and
- A vector of initial probabilities =(i)
 Model is represented by =(A, B, ).
},,,{ 21 Nsss 
},,,{ 21 Mvvv 
q1 q2 q3 q4 ……
1o 2o 3o 4o Observed
data

27. Specification of an HMM: 𝜆= (A,B,π)
27
number of observation

28. Hidden Markov Models Some Math.
28
With an observation sequence O=(o1 o2 … oT), state sequence
q=(q1 q2 … qT), and model  :
Probability of O, given state sequence q and model , is:
assuming independence between observations. This expands:
-- or --
The probability of the state sequence q can be written:


T
t
tt MqPMP
1
),|(),|( oqO
)|()|()|(),|( 2211 TT qpqpqpMP oooqO  
TT qqqqqqq aaaMP 132211
)|( 
 q
)()()(),|( 21 21 Tqqq T
bbbMP oooqO 

29. Hidden Markov Models Some Math.
29
The probability of both O and q occurring simultaneously is:
which can be expanded to:
)|(),|()|,( MPMPMP qqOqO 
)()()()|,( 1322211 211 Tqqqqqqqqqq TTT
baababMP oooqO  


30. Hidden Markov Models Example
30
Jar 1 Jar 2 Jar 3
S1 S2
0.3
0.2
0.6 0.6
S3
0.1
0.1
0.3
0.2
0.6
p(b) =0.8
p(w)=0.1
p(g) =0.1
p(b) =0.2
p(w)=0.5
p(g) =0.3
p(b) =0.1
p(w)=0.2
p(g) =0.7
State 3State 2State 1
1=0.33 2=0.33 3=0.33
 Example 1: Marbles in Jars

31. Hidden Markov Models Example cont.
31
 With the following observation
 What is probability of this observation, given state
sequence {S3 S2 S2 S1 S1 S3} and the model??
= b3(g) b2(w) b2(w) b1(b) b1(b) b3(g)
= 0.7 * 0.5 * 0.5 * 0.8 * 0.8 * 0.7
= 0.0784
g w w b b g
weather
Observation probability
b w g
s1 .8 .1 .1
s2 .2 .5 .3
s3 .1 .2 .7

32. Hidden Markov Models Example cont.
32
 With the same observation and different state sequence
 What is probability of this observation, given state
sequence {S1 S1 S3 S2 S3 S1} and the model??
= b1(g) b1(w) b3(w) b2(b) b3(b) b1(g)
= 0.1 * 0.1 * 0.2 * 0.2 * 0.1 * 0.1
= 0.000004
g w w b b g
weather
Observation probability
b w g
s1 .8 .1 .1
s2 .2 .5 .3
s3 .1 .2 .7

33. Hidden Markov Models
33
 Example 2: Weather and Atmospheric Pressure
0.3
0.3
0.6 0.2
0.1
0.1
0.6
0.5
0.3
P( )=0.1
P( )=0.2
P( )=0.8
H
P( )=0.3
P( )=0.4
P( )=0.3
M
L P( )=0.6
P( )=0.3
P( )=0.1
H = 0.4
M= 0.2
L = 0.4

34. Hidden Markov Models
34
What is probability of O={sun, sun, cloud, rain, cloud, sun}
and the sequence {H, M, M, L, L, M}, given the model?
= H·bH(s) ·aHM·bM(s) ·aMM·bM(c) ·aML·bL(r) ·aLL·bL(c) ·aLM·bM(s)
= 0.4 · 0.8 · 0.3 · 0.3 · 0.2 · 0.4 · 0.5 · 0.6 · 0.3 · 0.3 · 0.6 · 0.3
= 1.12x10-5
Today’s
State
Next State
H M L
H .6 .3 .1
M .3 .2 .5
L .1 .6 .3
State
Observation probability
rain cloud sun
H .1 .2 .8
M .3 .4 .3
L .6 .3 .1
H = 0.4
M= 0.2
L = 0.4

35. Hidden Markov Models
35
What is probability of O={sun, sun, cloud, rain, cloud, sun}
and the sequence {H, H, M, L, M, H}, given the model?
= H·bH(s) ·aHH·bH(s) ·aHM·bM(c) ·aML·bL(r) ·aLM·bM(c) ·aMH·bH(s)
= 0.4 · 0.8 · 0.6 · 0.8 · 0.3 · 0.4 · 0.5 · 0.6 · 0.6 · 0.4 · 0.3 · 0.8
= 3.19x10-4
Today’s
State
Next State
H M L
H .6 .3 .1
M .3 .2 .5
L .1 .6 .3
State
Observation probability
rain cloud sun
H .1 .2 .8
M .3 .4 .3
L .6 .3 .1
H = 0.4
M= 0.2
L = 0.4

36. Agenda
 Markov Chain & Markov Models
 Hidden Markov Model
 Main Issues Using HMMs:
• Evaluation
• Decoding
• Learning
36

37. Three classic HMM problems
• Evaluation
• Given a model and an output sequence ,
what is the probability that the model generated that output
• Decoding
• Given a model and an output sequence, what is the single
most likely state sequence (path) through the model that
produced that sequence?
• Learning
• Given a model and a set of observed sequences, what
should the model parameters be so that it has a high
probability of generating those sequences?
37

38. Main Issues Using HMMs
38
 Evaluation problem: Given the HMM M=(A, B, ) and the
observation sequence O=o1 o2 ... oK , calculate the probability
that model M has generated sequence O .
 Decoding problem: Given the HMM M=(A, B, ) and the
observation sequence O=o1 o2 ... oK , calculate the single most
likely sequence of hidden states si that produced this observation
sequence.
 Learning problem: Given some training observation sequences
O=o1 o2 ... oK and general structure of HMM (numbers of hidden
and visible states), determine HMM parameters M=(A, B, )
that best fit training data, that is maximizes P(O | M) .

39. The three main problems on HMMs
1. Evaluation
GIVEN a HMM , and a sequence O,
FIND Prob[ O |  ]
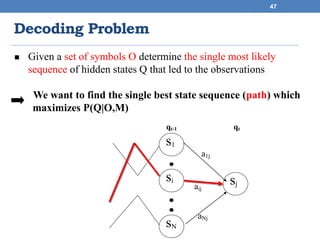
2. Decoding
GIVEN a HMM , and a sequence O,
FIND the sequence X of states that maximizes P[X | O,  ]
3. Learning
GIVEN a sequence O,
FIND a model  with parameters , A and B that
maximize P[ O |  ]

40. HMM Problems & Solutions
• Problem 1 (Evaluation): Likelihood of a sequence
• Forward Procedure
• Backward Procedure
• Problem 2 (Decoding): Best state sequence
• Viterbi Algorithm
• Problem 3 (Learning): Re-estimation
• Baum-Welch ( Forward-Backward Algorithm )

41. Agenda
 Markov Chain & Markov Models
 Hidden Markov Model
 Main Issues Using HMMs:
• Evaluation
• Learning
• Decoding
41

42. Central problems in HMM modelling
• Problem 1 Evaluation ( Naïve solution ) :
Given Observation Sequence O ={o1… oT}
Efficiently estimate P(O|λ)
• Useful in sequence classification
• Complicated
• It will take a long time.
because:
This is summed over all possible paths ( all possible state
sequences) if there is N states and their T times steps, total
number of paths is NT and each path costing O(T)
calculations.
the complexity = O(T NT) SO naïve is not good solution

43. Forward/Backward Algorithm
• Used for determining the parameters of an
HMM from training set data
• Calculates probability of going forward to a
given state (from initial state), and of
generating final model state (member of
training set) from that state
• Iteratively adjusts the model parameters
43

44. Agenda
 Markov Chain & Markov Models
 Hidden Markov Model
 Main Issues Using HMMs:
• Evaluation
• Learning
• Decoding
44

45. Learning Problem
Given a structure of the model, determine HMM
parameters M=(A, B, ) that best fit training data
determine these parameters
- Baum-Welch (Expectation-maximization, EM)Algorithm
• Often used to determine the HMM parameters
• Can also determine most likely path for a (set of) output
sequence(s)
• Add up probabilities over all possible paths
• Then re-update parameters and iterate
• Cannot guarantee global optimum; very expensive
45

46. Agenda
 Markov Chain & Markov Models
 Hidden Markov Model
 Main Issues Using HMMs:
• Evaluation
• Learning
• Decoding
46

47. Decoding Problem
47
 Given a set of symbols O determine the single most likely
sequence of hidden states Q that led to the observations
We want to find the single best state sequence (path) which
maximizes P(Q|O,M)
s1
si
sN
sjaij
aNj
a1j
qt-1 qt

48. Viterbi Algorithm
• Classical dynamic programming algorithm
• Choose “best” path (at each point), based on log-odds
scores
• Save results of “sub sub problems” and re-use them
as part of higher-level evaluations
• More efficient than Baum-Welch
48

49. Viterbi Algorithm
•
49
)o...o,o,sq,qP(qmax(i) t21it1-t1 t
𝜹t(i) is the highest probability of a state path for the partial
observation sequence O1O2O3…Ot such that the state Si.
The major difference from the forward algorithm:
Maximization instead of sum and additional backtracking

50. Thank You
50