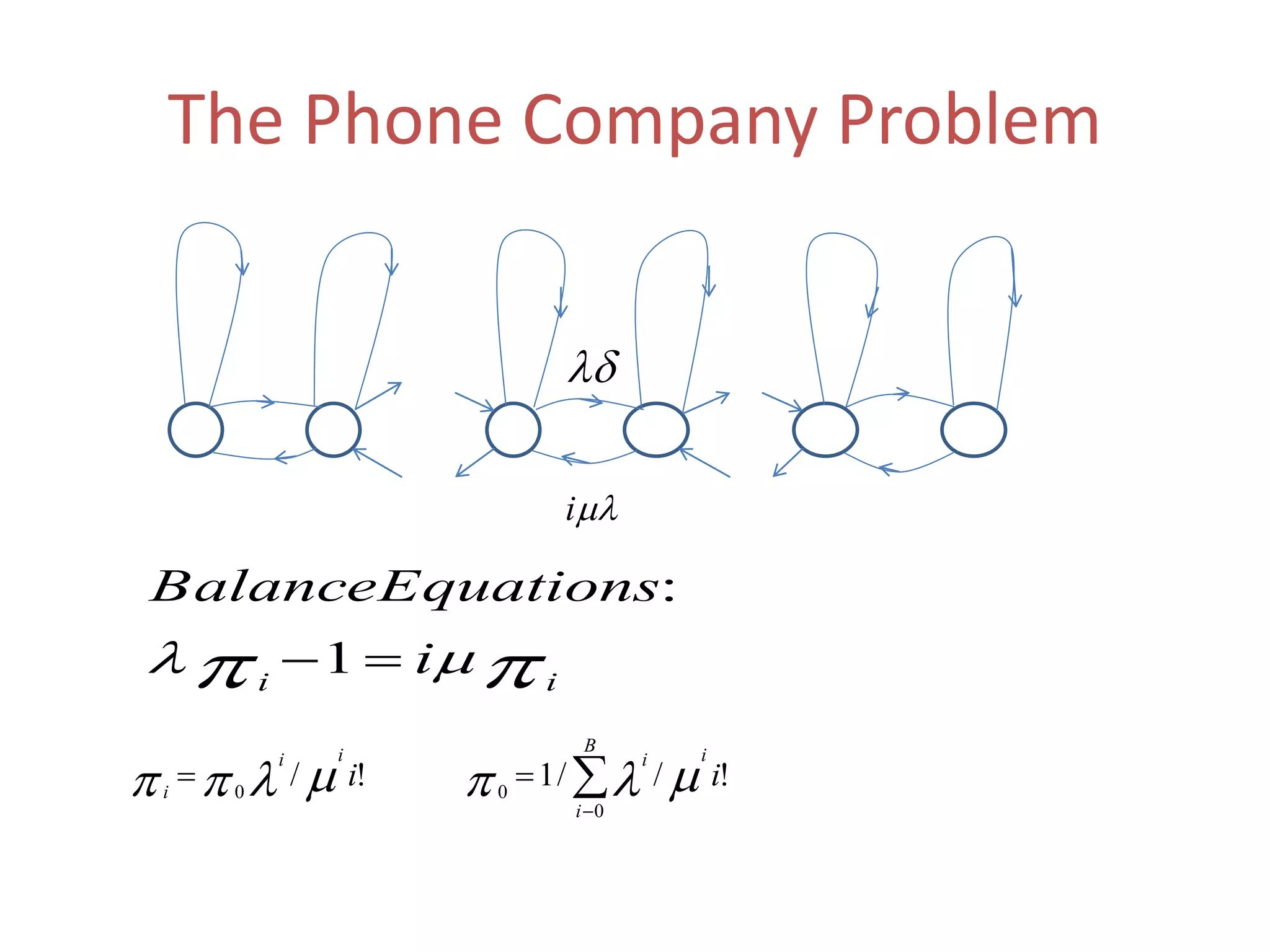
1. Markov processes can be used to model systems that transition between states based on probabilities. The document discusses several applications of Markov processes including calculating steady state probabilities, absorption probabilities, and expected times to absorption. 2. As an example, the document examines a phone company problem where calls arrive as a Poisson process and call durations are exponentially distributed. It shows how to set up and solve the balance equations to find steady state probabilities. 3. Other examples covered include finding the probability of an absent-minded professor getting wet during rain and calculating absorption probabilities and expected times for an example Markov chain. The document also discusses mean first passage and recurrence times.

1. Markov Processes-III
Presented by:

2. Outline
• Review of steady-state behavior
• Probability of blocked phone calls
• Calculating absorption probabilities
• Calculating expected time to absorption

3. Preview
• Assume a single class of recurrent states, a-periodic:
• Plus transient states, then
• Where Does not depend on the initial conditions
 jij
nn r  )()lim(
 j
 jn
ijn xx  )|()lim( 0

4. Preview
• Can be found as the unique solution to
the balance equations
• Together with
 m
1
mj
k
kjkj P 1,  
 
j
j
1

5. Example
1 2
7/5,7/2 21
 
5.0 5.0
8.0
2.0

6. Example
• Assume that process starts as state 1
)99()1,1( 11111001 rPxx andP 
prxx andP
1211101100
)100()21( 

7. The Phone Company Problem
• Calls originate as a poison process, rate
 Each call duration is exponentially distributed(parameter
 B lines available
• Discrete time intervals of( small) length




8. The Phone Company Problem
  ii
i
EquationsBalance
1
:


B
i
iiii
i
ii
0
00
!//1!/ 

i

9. Steady State Probability:
Example#1
• Consider a Markov chain with given transition
probabilities and with a single recurrent class
which is a-periodic
• Assume that for the n-step transition
probabilities are very close to steady state
probabilities
• Find
500n
 lJKJjkij PPr
XXXX ilkJP


)1000(
)|,,( 0200010011000

10. Steady State Probability:
Example#1
• B)
• Solution:
• By using Bay’s Rule:
?/( 10011000
 jiP XX
 jiji P
XXXXX jPjiPjiP
/
)(/),()/( 10011001100010011000



11. Steady State Probability:
Example#2
• An absent minded professor has two
umbrellas that she uses when coming from
home to office and back. If it rains and
umbrella is available in her location, she takes
it. If it is not raining, she always forget to take
an umbrella. Suppose it rains with probability
‘P’ each time comes, independently of other
times, what is the steady state probability that
she wet during a rain?

12. Steady State Probability:
Example#2
• Markov mode with following states:
• State ‘i’ where i=0,1,2
• ‘i’ umbrellas are available in current location
• Transition probability matrix:
01
10
100
pp
pp



13. Steady State Probability:
Example#2
• The chain has single recurrent class which is a-
periodic
• So, steady state convergence theorem applies.
0 2 1
p1
p1 p
p
1

14. Steady State Probability:
Example#2
• Balance Equations are as below:
1
)1(
)1(
021
102
211
20








p
pp
p

15. Steady State Probability
Example#2
• After Solving:
• So, the steady state probability that she gets
wet is times the probability of rain=
)3(/1
)3(/1
)3(/)1(
1
1
0
p
p
pp






0
p0

16. Calculating Absorption Probabilities
• What is the probability that: process eventually settles in
state 4, given that the initial state is i?
ai
3
2
5
4
1
1
1
2.0
2.0
3.0
4.0
5.0
6.0
8.0

17. Calculating Absorption Probabilities
SolutionuniqueiotherallFor
iFor
iFor
apa
a
a
j
j
iji
i
i



0,5
1,4

18. Expected time to absorption
• Find expected number of transitions until reaching the
Absorbing state, given that
the initial state is i?
3
2
4
1
1
2.0
5.0
4.0
5.0
6.0
8.0
i

19. Expected Time to Absorption
SolutionuniqueiotherallFor
ifor
j
jiji
i
p



1:
40

20. Absorption Probabilities
Example#1
• Consider the Markov Chain

21. Mean First Passage and Recurrence
Times
• Chain with one recurrent class;
• Fix s recurrent
• Mean first passage time from s to i
 


j
jiji
s
m
ni
siallfor
tosolutionuniquetheare
isthatsuchnE
tpt
t
ttt
XXt
1
0
,.
]|}0[min{
21
0


22. Mean First Passage and Recurrence
Times
• Mean recurrence time of s:




p
ssthatsuchnE
aj
j js
ns
tt
XXt
1
]|}1[min{ 0