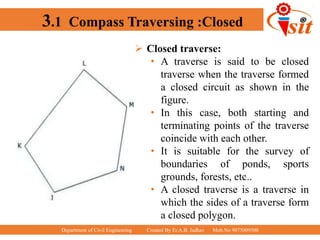
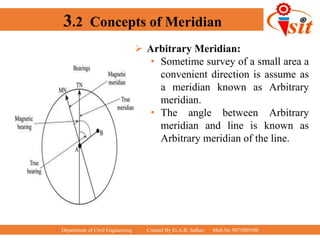
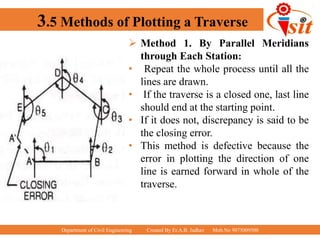
The document discusses compass traversing and the components of a prismatic compass used for surveying. It describes open and closed traverses, different types of meridians (true, magnetic, arbitrary), concepts of bearing (whole circle, quadrantal, fore, back), and components of the prismatic compass including the magnetic needle, graduated circle, prism, object vane, eye vane, and glass cover. The document is intended to teach basic surveying concepts and the use of a prismatic compass for taking measurements in the field.