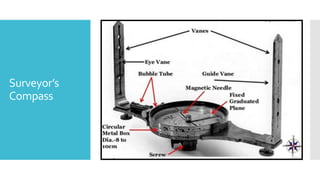
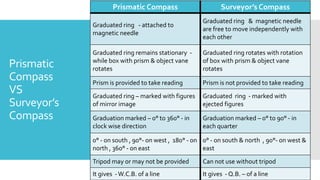
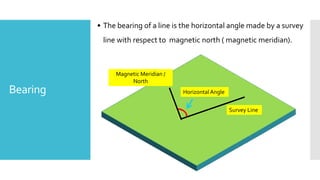
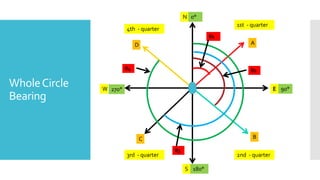
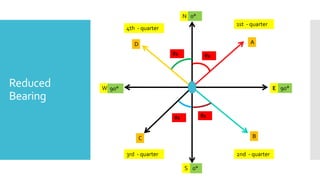
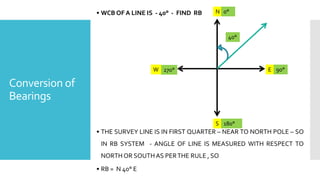
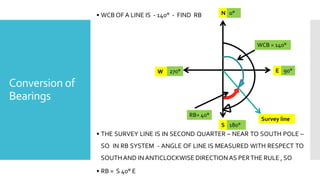
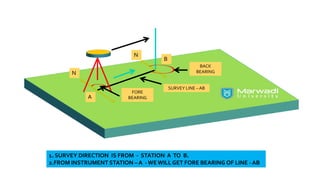
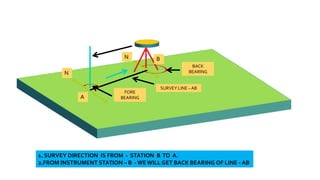
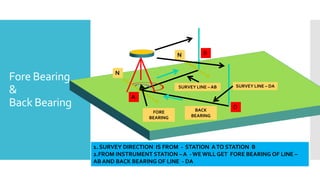
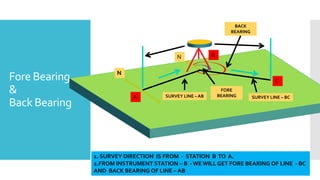
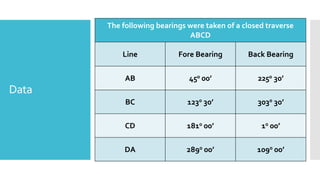
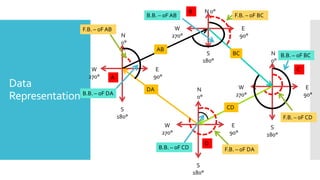
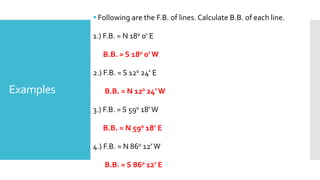
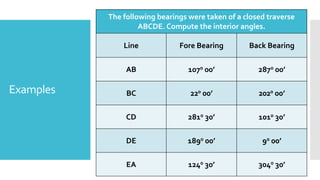
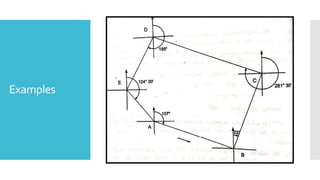
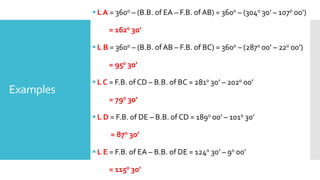
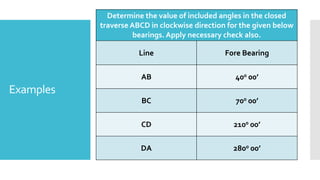
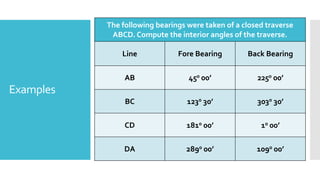
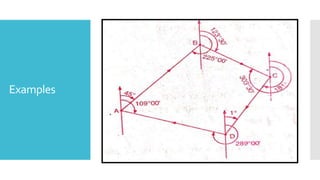
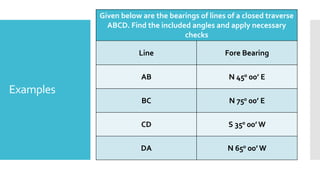
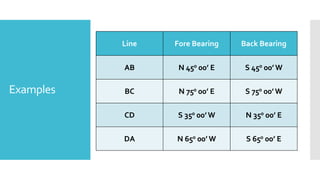
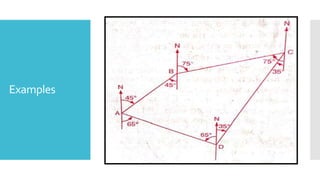
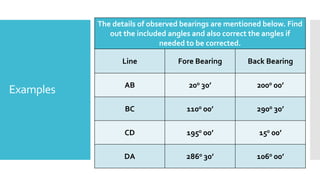
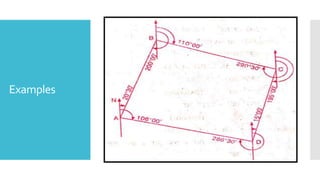
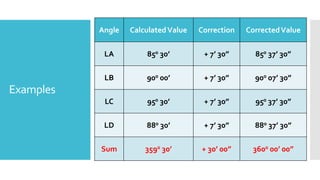
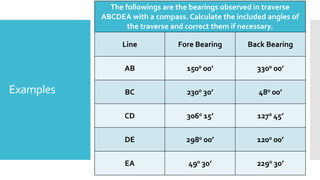
This document provides a disclaimer for content used in a YouTube channel's videos. It states that the content is meant for non-commercial, educational purposes only. It acknowledges that some images used may be under copyright but their use was unintentional and for fair use only. The document says that any copyrighted material will be removed if a claim is received.

1. Disclaimer
It is hereby declared that the production of the said content is meant for
non-commercial, scholastic and research purposes only.
We admit that some of the content or the images provided in this channel's
videos may be obtained through the routine Google image searches and few of
them may be under copyright protection. Such usage is completely inadvertent.
It is quite possible that we overlooked to give full scholarly credit to the Copyright
Owners. We believe that the non-commercial, only-for-educational use of the
material may allow the video in question fall under fair use of such content.
However we honour the copyright holder's rights and the video shall be deleted
from our channel in case of any such claim received by us or reported to us.

2. Department of Civil
Engineering
Jay Kirit Kalaria
Unit No - 3
Unit Title – Angular
Measurement
Subject Name – Basic Civil
Engineering
Code – 3110004

3. Angular
Measurement
ANGULAR
MEASUREMENT
2.
TYPES AND
USE OF
COMPASS
3.
BEARINGS
4.
SYSTEMOF
BEARING
5.
COMPUTATION
OF ANGLES
6.
TRUE BEARING &
MAGNETIC
BEARING
7.
LOCAL
ATTRACTION
1. INTRODUCTION

4. Compass
Survey
• When survey area is large, undulated and having more no. of
details in it – in that case it is not possible to adopt chain
surveying (to divide area in to network of triangles).
• In such situation - for survey - method of traversing is
adopted.
• In traversing – framework consist of a number of connected
survey lines
• Length – of survey line is measured by chain or tape and the
direction of survey line is measured by – magnetic compass
• This type of survey - is called compass survey or compass
traversing.

5. Traverse A
E
D
C
B

6. Types of
Compass
• Prismatic compass
• Surveyor’s compass

7.  Civl 5 6 7 16 20 24 25 27 28 31 32 33 34 35 36 38 39 40 41 42 43 44
45 46 48 50 53 55 58 61 63 66
 Me
 2 9 12 14 16 17 21 27
 Chem
 1 7 10 11 14 22 23
 Auto
 7

8. Prismatic
Compass
• Main parts of prismatic compass are:
 Cylindrical metal box
 Pivot
 Lifting pin & lifting lever
 Magnetic needle
 Graduated circle or ring
 Prism
 Object van
 Eye vane
 Glass cover
 Sun glass
 Reflecting mirror
 Spring brake or brake pin

9. Surveyor’s
Compass

10. Working of
Prismatic
Compass
• Prismatic compass is mounted on light tripod stand - having
vertical spindle in the ball and socket arrangement - to
which compass is fixed.
• Working or temporary adjustment of prismatic compass -
involves 3 steps.
• Before taking reading with prismatic compass
1) Centering
2) Leveling
3) Focusing …. Is required to be done
• After performing above three steps - bearing of a line is
observed.

11. Prismatic
Compass
VS
Surveyor’s
Compass
Prismatic Compass Surveyor’s Compass
Graduated ring - attached to
magnetic needle
Graduated ring & magnetic needle
are free to move independently with
each other
Graduated ring remains stationary -
while box with prism & object vane
rotates
Graduated ring rotates with rotation
of box with prism & object vane
rotates
Prism is provided to take reading Prism is not provided to take reading
Graduated ring – marked with figures
of mirror image
Graduated ring - marked with
ejected figures
Graduation marked – 0° to 360° - in
clock wise direction
Graduation marked – 0° to 90° - in
each quarter
0° - on south , 90°- on west , 180° - on
north , 360° - on east
0° - on south & north , 90°- on west &
east
Tripod may or may not be provided Can not use without tripod
It gives -W.C.B. of a line It gives - Q.B. – of a line

12.  CIVIL 3 10 13 14 51 56 64 15
 ME 1 4 7 10 20 22 11 24 22 28 29 33 8
 Auto 1 3 4
 Che 2 3 5 6 16

13.  CIVIL 2 3 8 9 10 13 14 51 56 64 15 62 64 59
 ME 1 4 7 10 20 22 11 24 22 29 8 30 5 25 6 26 3
 Auto 1 3 4
 Che 2 5 6 16 15 4 17

14. Bearing
Magnetic Meridian /
North
Survey Line
Horizontal Angle
• The bearing of a line is the horizontal angle made by a survey
line with respect to magnetic north ( magnetic meridian).

15. Types of
Bearings
• Types of bearing - based upon meridian
1.True bearing:
 It is a horizontal angle between -true meridian and survey
line
 It is measured from -true north in clock wise direction
2. Magnetic bearing:
 It is a horizontal angle between -magnetic north and survey
line
3. Grid bearing:
 It is a horizontal angle between - grid meridian and survey
line
4. Arbitrary bearing:
 It is a horizontal angle between - arbitrary meridian and
survey line

16. System of
Bearings
• Whole Circle Bearing
• Reduced Bearing or Quadrantal Bearing System

17.  CIVIL 1 5 6 7 16 20 25 26 27 28 31 32 33 35 36 38 39 40 42 43 44 45
46 48 50 61 63 60 27
 ME 2 9 12 14 27 31
 AUTO 7 8
 CHE 1 14 10 11 23

18. WholeCircle
Bearing
• Bearing of a line measured with respect to magnetic
meridian in clockwise direction.
• Value - 0° to 360°
• Quarter start form - North – progress in clockwise direction.
• First - 0° to 90° , second - 90° to 180° , third - 180° to 270°,
fourth - 270° to 360°.
• As per the figure – A,B,C, & D - station - in quarter - 1st , 2nd
, 3rd , & 4th.
• ThenW.C.B. of line - OA = θ1
OB = θ2
OC = θ3
OD = θ4

19. WholeCircle
Bearing
N
W
S
E
270°
180°
90°
0°
1st - quarter
2nd - quarter
3rd - quarter
4th - quarter
D
C B
A
θ3
θ4 θ2
θ1

20. Reduced
Bearing
• When whole circle bearing of a line is converted into -
quadrant bearing - it is called reduced bearing.
• It is similar to Q.B. – value varies between – 0° to 90°.
• In this system - quarter should be mentioned for proper
designation.

21. Reduced
Bearing
N
W
S
E
90°
0°
90°
0°
1st - quarter
2nd - quarter
3rd - quarter
4th - quarter
D
C B
A
θ1
θ1 θ1
θ1

22. Conversion of
Bearings
W.C.B. – of
Any Line
Quarter in
Which it
Lies
Rule Quarter
0° to 90° I RB = WCB N –E
90° to 180° II RB = 180° - WCB S – E
180° to 270° III RB = WCB - 180° S – W
270° to 360° IV RB = 360° - WCB N – W

23. Conversion of
Bearings
N
W
S
E
40°
270°
180°
90°
0°
• WCB OF A LINE IS - 40° - FIND RB
• THE SURVEY LINE IS IN FIRST QUARTER – NEAR TO NORTH POLE – SO
IN RB SYSTEM - ANGLE OF LINE IS MEASURED WITH RESPECT TO
NORTH OR SOUTHAS PERTHE RULE , SO
• RB = N 40° E

24. Conversion of
Bearings
N
W
S
E
WCB = 140°
270°
180°
90°
0°
RB= 40°
Survey line
• WCB OF A LINE IS - 140° - FIND RB
• THE SURVEY LINE IS IN SECOND QUARTER – NEAR TO SOUTH POLE –
SO IN RB SYSTEM - ANGLE OF LINE IS MEASURED WITH RESPECT TO
SOUTHAND INANTICLOCKWISE DIRECTIONAS PERTHE RULE , SO
• RB = S 40° E

25. Fore Bearing &
Back Bearing
• FORE BEARING:
 Bearing of a line measured in the forward direction of survey
line - is known as fore bearing.
• BACK BEARING:
 Bearing of a line measured in the backward ( opposite)
direction of survey line - is known as back bearing.

26. N
N
B
A
FORE
BEARING
BACK
BEARING
1. SURVEY DIRECTION IS FROM - STATION A TO B.
2.FROM INSTRUMENT STATION – A - WE WILL GET FORE BEARING OF LINE - AB
SURVEY LINE – AB

27. N
N B
A
FORE
BEARING
BACK
BEARING
1. SURVEY DIRECTION IS FROM - STATION B TO A.
2.FROM INSTRUMENT STATION – B - WE WILL GET BACK BEARING OF LINE - AB
SURVEY LINE – AB

28. Fore Bearing
&
Back Bearing
N
N B
A
FORE
BEARING
BACK
BEARING
1. SURVEY DIRECTION IS FROM - STATION ATO STATION B
2.FROM INSTRUMENT STATION – A - WE WILL GET FORE BEARING OF LINE –
AB AND BACK BEARING OF LINE - DA
SURVEY LINE – AB
D
SURVEY LINE – DA

29. Fore Bearing
&
Back Bearing
N
N B
A
FORE
BEARING
BACK
BEARING
1. SURVEY DIRECTION IS FROM - STATION B TO A.
2.FROM INSTRUMENT STATION – B - WE WILL GET FORE BEARING OF LINE - BC
AND BACK BEARING OF LINE – AB
SURVEY LINE – AB
C
SURVEY LINE – BC

30. Data
The following bearings were taken of a closed traverse
ABCD
Line Fore Bearing Back Bearing
AB 450 00’ 2250 30’
BC 1230 30’ 3030 30’
CD 1810 00’ 10 00’
DA 2890 00’ 1090 00’

31.  1 5 6 7 20 24 28 27 3031 32 33 34 35 36 38 39 40 41 42 43 44 45 46 48
49 50 53 55 58 61
 Me 2 12 14 16 17 21 27
 Auto 7 8
 Che
 1 7 10 11 14 18 22 23

32. Data
Representation
N
0°
W
270°
S
180°
E
90°
N 0°
W
270°
S
180°
E
90°
N
0°
W
270°
S
180°
E
90°
N
0°
W
270°
S
180°
E
90°
A
DA
CD
BC
AB
D
C
B
F.B. – 0F AB
F.B. – 0F DA
F.B. – 0F CD
F.B. – 0F BC
B.B. – 0F DA
B.B. – 0F CD
B.B. – 0F BC
B.B. – 0F AB

33. Conditions for
Determining
B.B.
ForWCB System:
If F.B. is less than 1800,
B.B. = F.B. + 1800
If F.B. is more than 1800,
B.B. = F.B. – 1800
For RB or QB System:
F.B. and B.B. have equal numerical values, but in opposite
directions.
So angle remains same but direction will be opposite.

34. Examples
Following are the observed fore bearings of lines. Find their
back bearings.
1.) F.B. = 120 24’
Here F.B. is less than 1800, therefore B.B. = F.B. + 1800
= 120 24’ + 1800
B.B. = 1920 24’
2.) F.B. = 1190 48’
Here F.B. is less than 1800, therefore B.B. = F.B. + 1800
= 1190 48’ + 1800
B.B. = 2990 48’

35. Examples
3.) F.B. = 2660 30’
Here F.B. is more than 1800, therefore B.B. = F.B. - 1800
= 2660 30’ - 1800
B.B. = 860 30’
4.) F.B. = 3540 18’
Here F.B. is more than 1800, therefore B.B. = F.B. - 1800
= 3540 18’ - 1800
B.B. = 1740 18’

36. Examples
Following are the F.B. of lines. Calculate B.B. of each line.
1.) F.B. = N 180 0’ E
B.B. = S 180 0’ W
2.) F.B. = S 120 24’ E
B.B. = N 120 24’ W
3.) F.B. = S 590 18’W
B.B. = N 590 18’ E
4.) F.B. = N 860 12’W
B.B. = S 860 12’ E

37. Meridians
 Bearing of a line - always measured in clockwise with respect
to some reference line or direction , - this fixed reference line is
known as meridian.
 Three types of meridian:-
 Magnetic meridian:-
 Direction shown by a freely suspended needle which is
magnetized and balanced properly without influenced
by any other factors
 True meridian:-
 True meridian is a line which passes through -true
north and south.
 Can be determined by observing bearing of sun at 12
noon
 Arbitrary meridian:-
 In case of small work or place where true meridian or
magnetic meridian cannot be determined
 Any direction of a permanent object is taken as a
reference direction - called as arbitrary meridian.

38. Local
Attraction
 When prismatic compass – centered on any station – needle
shows – magnetic meridian / magnetic north( north direction)
 But , when centered near by - iron or steel structures , under
electric cable of high voltage current - magnetic needle of
compass will not show – magnetic north but is deflected from its
normal location.
 That means - magnetic needle is under the influence of the some
external force
 This deviation of needle form the magnetic north (its original
location) under the influence of magnetic force - known as -
LOCAL ATTRACTION.
 Bearing measured from such station are not - correct and
required to be correct to plot the traverse

39. Sources of
Local
Attraction
Natural sources : - iron ores , magnetic rocks , etc.
Artificial sources : - steel structures , rails, iron pipes , electric
lines ,metal pieces ,chains , arrows , ranging rods , bunch of
keys in hand & pocket.

40. Detection of
Local
Attraction
 Fore and back bearing of a line is taken.
 If the difference of fore and back bearing of a line is exactly - 180° , -
NO LOCAL ATTRACTION.
 If the difference of fore and back bearing of a line is OTHER THEN -
180° , - NEEDLE IS UNER THE INFLUENCCE OF LOCAL
ATTRACTION.
 To balance the effect of local attraction – amount of error is found out
and is equally distributed between – fore and back bearing of the line.
 EXAMPLE : -
 Observed FB of line AB – 70° 30’
 Observed BB of line AB - 250° 00’
 Difference of BB & FB = (250° 00’ - 70° 30’) = 179° 30’

41. Detection of
Local
Attraction
 Difference of BB & FB = (250° 00’ - 70° 30’) = 179° 30’
 Means - there is local attraction.
 Amount of error = (180° 00’-179° 30’) = 30’
 So, distribute - error equally in FB & BB - of line AB.
 Means - 30’/2 = 15’ – will required to be adjusted in each bearing
 If in FB – error is added - then in BB - error is subtracted
 If in FB – error is subtracted - then in BB - error is added
 So that difference between - FB & BB of line AB – must be - 180°.
 For our case - subtract the error of - 15’ from – FB and add error of
15’ in BB of line AB
 So , Corrected FB – of line AB = (70° 30’-15’) = 70° 15’
 Corrected BB of line AB = (250° 00’ +15’) = 250° 15’
 Now difference of FB & BB – of line AB
 =(250° 15’ -70° 15’)= 180°

42. Method of
Application of
Correction
1) First Method:
 Internal angles - are calculated from observed bearing
 Check is applied - sum of internal angles should be equal to (2n-4) X 90°
 If not total error is equally distributed among all the angles
 Then form starting form the unaffected line - bearings of other lines are
corrected from corrected internal angles
1) Second Method:
 From the given bearing - unaffected line is first detected
 Then form unaffected line - bearing of other affected lines are corrected by
finding amount of error at each station.
 If all the lines are affected by local attraction –line with minimum error is
identified
 FB & BB of this line are adjusted by distributing error equally ( making
difference of FB & BB = 180°)
 Then from line FB & BB of other lines are corrected.

43. Examples
The following bearings were taken of a closed traverse
ABCDE. Compute the interior angles.
Line Fore Bearing Back Bearing
AB 1070 00’ 2870 00’
BC 220 00’ 2020 00’
CD 2810 30’ 1010 30’
DE 1890 00’ 90 00’
EA 1240 30’ 3040 30’

44. Examples

46. Examples
L A = 3600 – (B.B. of EA – F.B. of AB) = 3600 – (3040 30’ – 1070 00’)
= 1620 30’
L B = 3600 – (B.B. ofAB – F.B. of BC) = 3600 – (2870 00’ – 220 00’)
= 950 30’
L C = F.B. of CD – B.B. of BC = 2810 30’ – 2020 00’
= 790 30’
L D = F.B. of DE – B.B. of CD = 1890 00’ – 1010 30’
= 870 30’
L E = F.B. of EA – B.B. of DE = 1240 30’ – 90 00’
= 1150 30’

47. Examples
Check:
1.) Sum of interior angles = (2N – 4) × 900
= (2 × 5 - 4) × 900 = 5400 (Where, N = No. of Angles)
2.) LA + LB + LC + LD + LE = 1620 30’ + 950 00’ + 790 30’ + 870 30’ +
1150 30’
= 5400
Therefore, OK

48. Examples
Determine the value of included angles in the closed
traverse ABCD in clockwise direction for the given below
bearings. Apply necessary check also.
Line Fore Bearing
AB 400 00’
BC 700 00’
CD 2100 00’
DA 2800 00’

49. Examples
Line Fore Bearing Back Bearing
AB 400 00’ 2200 00’
BC 700 00’ 2500 00’
CD 2100 00’ 300 00’
DA 2800 00’ 1000 00’

50. Examples

51. Examples
L A = B.B. of DA – F.B. of AB = 1000 00’ – 400 00’
= 600 00’
L B = B.B. ofAB – F.B. of BC = 2200 00’ – 700 00’
= 1500 00’
L C = B.B. of BC – F.B. of CD = 2500 00’ – 2100 00’
= 400 00’
L D = 3600 – (F.B. of DA – B.B. of CD) = 3600 – (2800 00’ – 300 00’)
= 1100 00’

52. Examples
Check:
1.) Sum of interior angles = (2N – 4) × 900
= (2 × 4 - 4) × 900 = 3600 (Where, N = No. of Angles)
2.) LA + LB + LC + LD = 600 00’ + 1500 00’ + 400 00’ + 1100 00’
= 3600
Therefore, OK

53. Examples
The following bearings were taken of a closed traverse
ABCD. Compute the interior angles of the traverse.
Line Fore Bearing Back Bearing
AB 450 00’ 2250 00’
BC 1230 30’ 3030 30’
CD 1810 00’ 10 00’
DA 2890 00’ 1090 00’

54. Examples

55. Examples
L A = B.B. of DA – F.B. of AB = 1090 00’ – 450 00’
= 640 00’
L B = B.B. ofAB – F.B. of BC = 2250 00’ – 1230 30’
= 1010 30’
L C = B.B. of BC – F.B. of CD = 3030 30’ – 1810 00’
= 1220 30’
L D = 3600 – (F.B. of DA – B.B. of CD) = 3600 – (2890 00’ – 10 00’)
= 720 00’

56. Examples
Check:
1.) Sum of interior angles = (2N – 4) × 900
= (2 × 4 - 4) × 900 = 3600 (Where, N = No. of Angles)
2.) LA + LB + LC + LD = 640 00’ + 1010 30’ + 1220 30’ + 720 00’
= 3600
Therefore, OK

57. Examples
Given below are the bearings of lines of a closed traverse
ABCD. Find the included angles and apply necessary
checks
Line Fore Bearing
AB N 450 00’ E
BC N 750 00’ E
CD S 350 00’ W
DA N 650 00’ W

58. Examples
Line Fore Bearing Back Bearing
AB N 450 00’ E S 450 00’ W
BC N 750 00’ E S 750 00’ W
CD S 350 00’ W N 350 00’ E
DA N 650 00’ W S 650 00’ E

59. Examples

60. Examples
L A = 1800 – (F.B. ofAB + B.B. of DA) = 1800 – (450 00’ + 650 00’)
= 700 00’
L B = (1800 – F.B. of BC) + B.B. of AB = (1800 – 750 00’) + 450 00’
= 1500 00’
L C = B.B. of BC – F.B. of CD = 750 00’ – 350 00’
= 400 00’
L D = B.B. of CD + F.B. of DA = 350 00’ + 650 00’
= 1000 00’

61. Examples
Check:
1.) Sum of interior angles = (2N – 4) × 900
= (2 × 4 - 4) × 900 = 3600 (Where, N = No. of Angles)
2.) LA + LB + LC + LD = 700 00’ + 1500 00’ + 400 00’ + 1000 00’
= 3600
Therefore, OK

62. Examples
The details of observed bearings are mentioned below. Find
out the included angles and also correct the angles if
needed to be corrected.
Line Fore Bearing Back Bearing
AB 200 30’ 2000 00’
BC 1100 00’ 2900 30’
CD 1950 00’ 150 00’
DA 2860 30’ 1060 00’

63. Examples

64. Examples
L A = B.B. of DA – F.B. of AB = 1060 00’ – 200 30’
= 850 30’
L B = B.B. ofAB – F.B. of BC = 2000 00’ – 1100 00’
= 900 00’
L C = B.B. of BC – F.B. of CD = 2900 30’ – 1950 00’
= 950 30’
L D = 3600 – (F.B. of DA – B.B. of CD) = 3600 – (2860 30’ – 150 00’)
= 880 30’

65. Examples
Check:
1.) Sum of interior angles = (2N – 4) × 900
= (2 × 4 - 4) × 900 = 3600 (Where, N = No. of Angles)
2.) LA + LB + LC + LD = 850 30’ + 900 00’ + 950 30’ + 880 30’
= 3590 30’
Therefore,Total Error = 3590 30’ – 3600 00’ = - 30’
Therefore,Total Correction = + 30’
Therefore, Correction per Angle = +
30′
4
= + 7’ 30”

66. Examples
Angle CalculatedValue Correction CorrectedValue
LA 850 30’ + 7’ 30” 850 37’ 30”
LB 900 00’ + 7’ 30” 900 07’ 30”
LC 950 30’ + 7’ 30” 950 37’ 30”
LD 880 30’ + 7’ 30” 880 37’ 30”
Sum 3590 30’ + 30’ 00” 3600 00’ 00”

67.  Civil 31 28 33 43 35 39 46
 Me 2 17
 Che 14
 Auto All Absent

68. Examples
The followings are the bearings observed in traverse
ABCDEA with a compass. Calculate the included angles of
the traverse and correct them if necessary.
Line Fore Bearing Back Bearing
AB 1500 00’ 3300 00’
BC 2300 30’ 480 00’
CD 3060 15’ 1270 45’
DE 2980 00’ 1200 00’
EA 490 30’ 2290 30’

69. Examples

70. Examples
L A = B.B. of EA – F.B. of AB = 2290 30’ – 1500 00’
= 790 30’
L B = B.B. ofAB – F.B. of BC = 3300 00’ – 2300 30’
= 990 30’
L C = 3600 – (F.B. of CD – B.B. of BC) = 3600 – (3060 15’ – 480 00’)
= 1010 45’
L D = 3600 – (F.B. of DE – B.B. of CD) = 3600 – (2980 00’ – 1270 45’)
= 1890 45’
L E = B.B. of DE – F.B. of EA = 1200 00’ – 490 30’
= 700 30’

71. Examples
Check:
1.) Sum of interior angles = (2N – 4) × 900
= (2 × 5 - 4) × 900 = 5400 (Where, N = No. of Angles)
2.) LA + LB + LC + LD + LE = 790 30’ + 990 30’ + 1010 45’ + 1890 45’ +
700 30’
= 5410 00’
Therefore,Total Error = 5410 00’ – 5400 00’ = + 10
Therefore,Total Correction = - 10 = - 60’
Therefore, Correction per Angle = -
60′
5
= - 12’

72. Examples
Angle CalculatedValue Correction CorrectedValue
LA 790 30’ - 12’ 790 18’
LB 990 30’ - 12’ 990 18’
LC 1010 45’ - 12’ 1010 33’
LD 1890 45’ - 12’ 1890 33’
LE 700 30’ - 12’ 700 18’
Sum 5410 00’ - 60’ 5400 00’