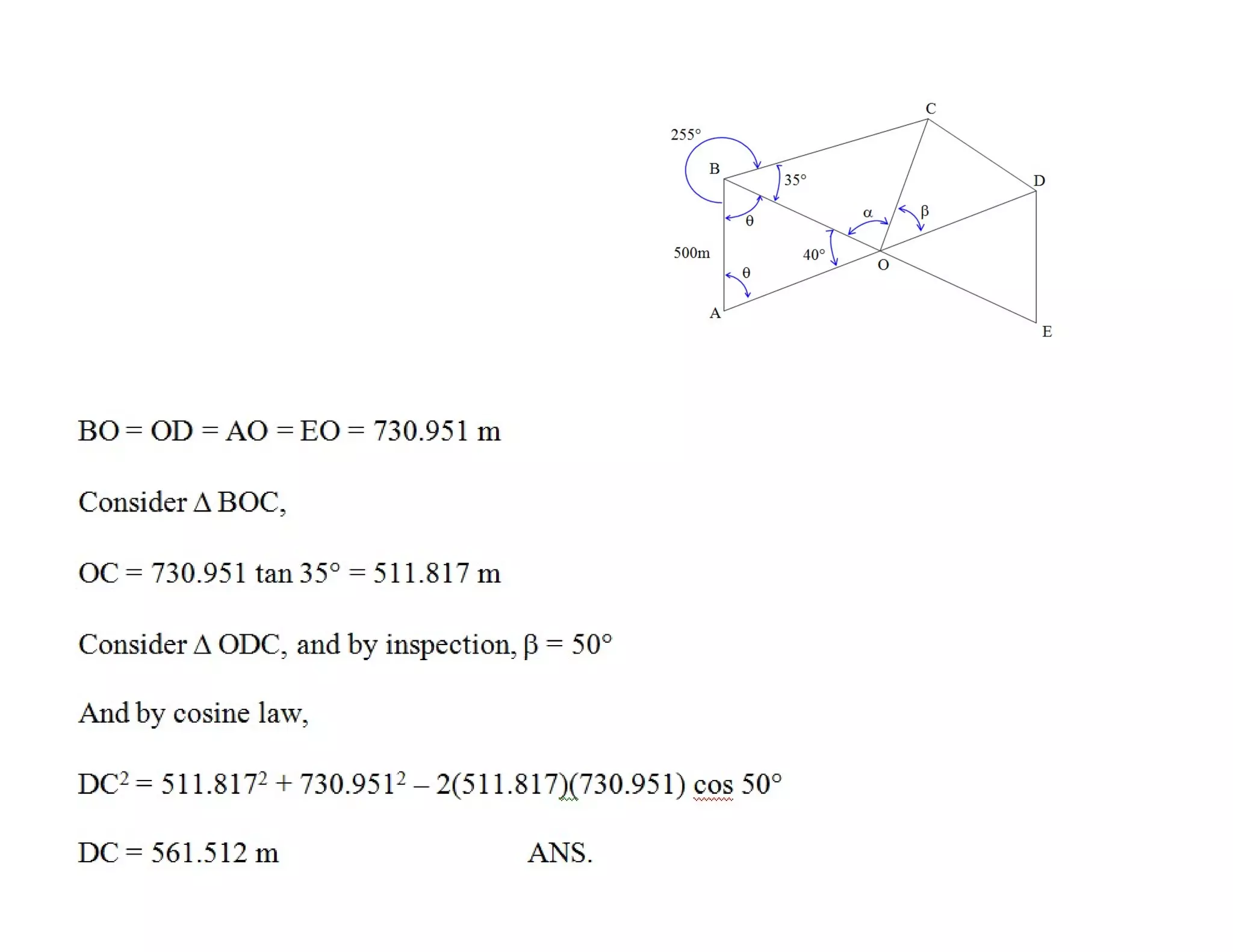
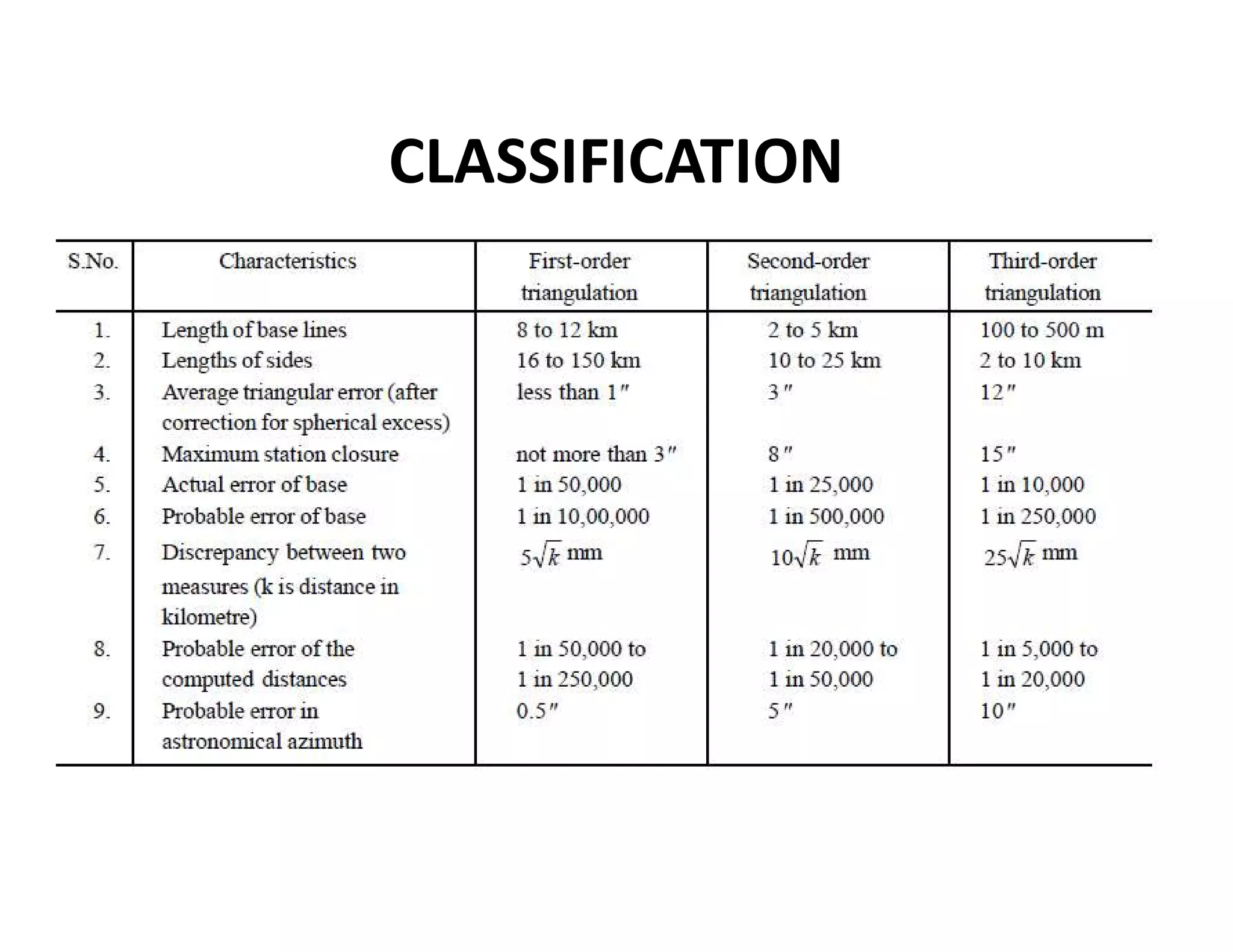
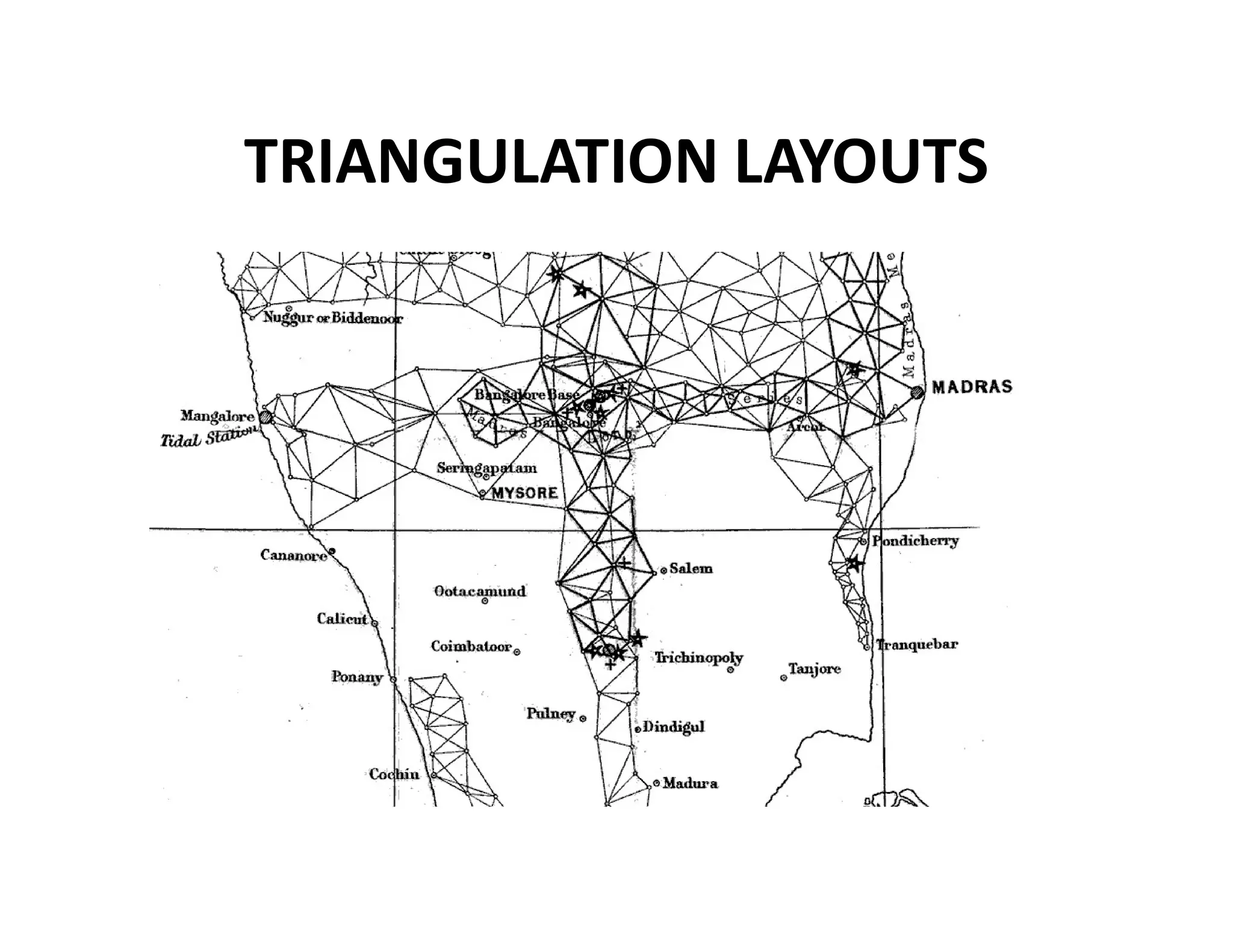
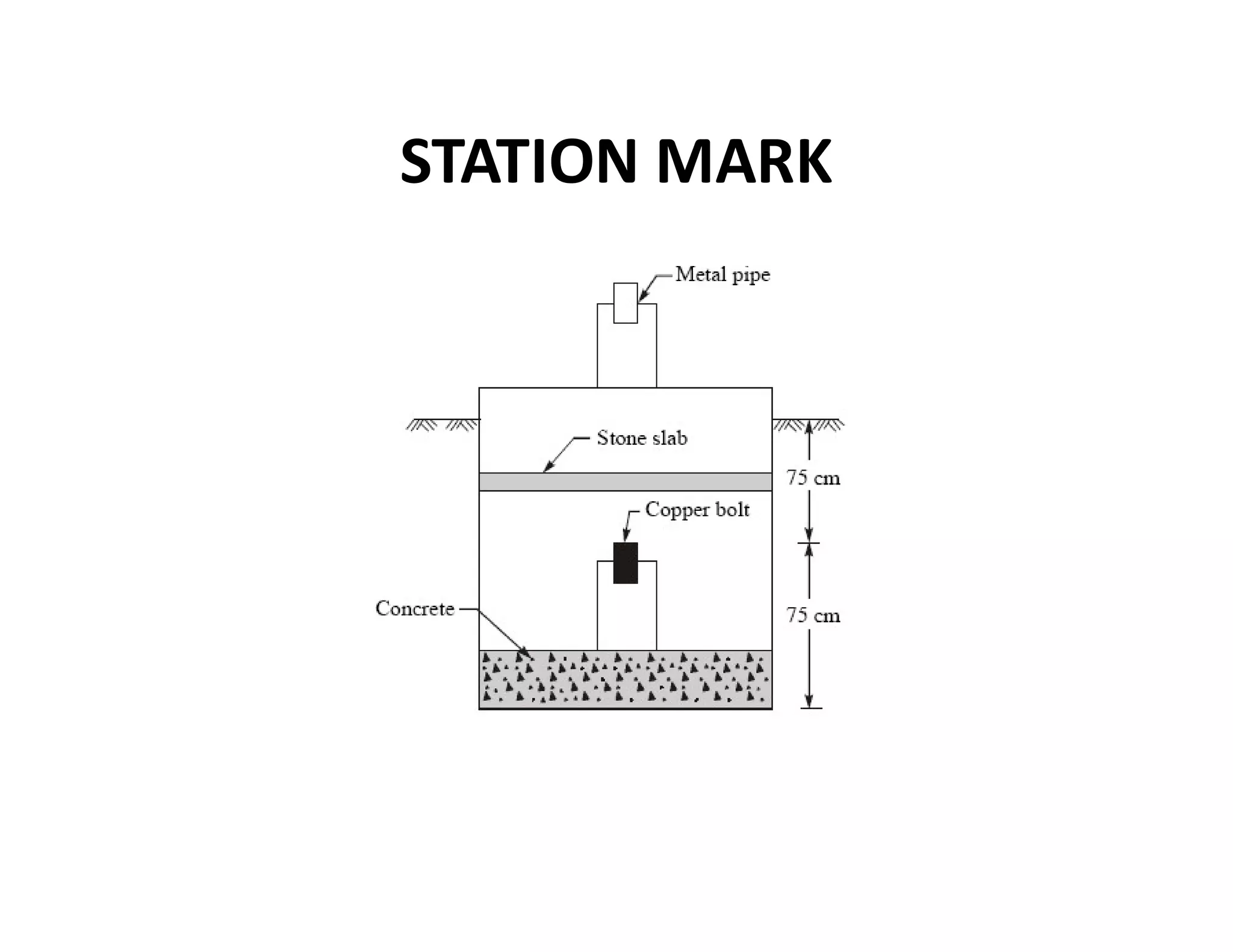
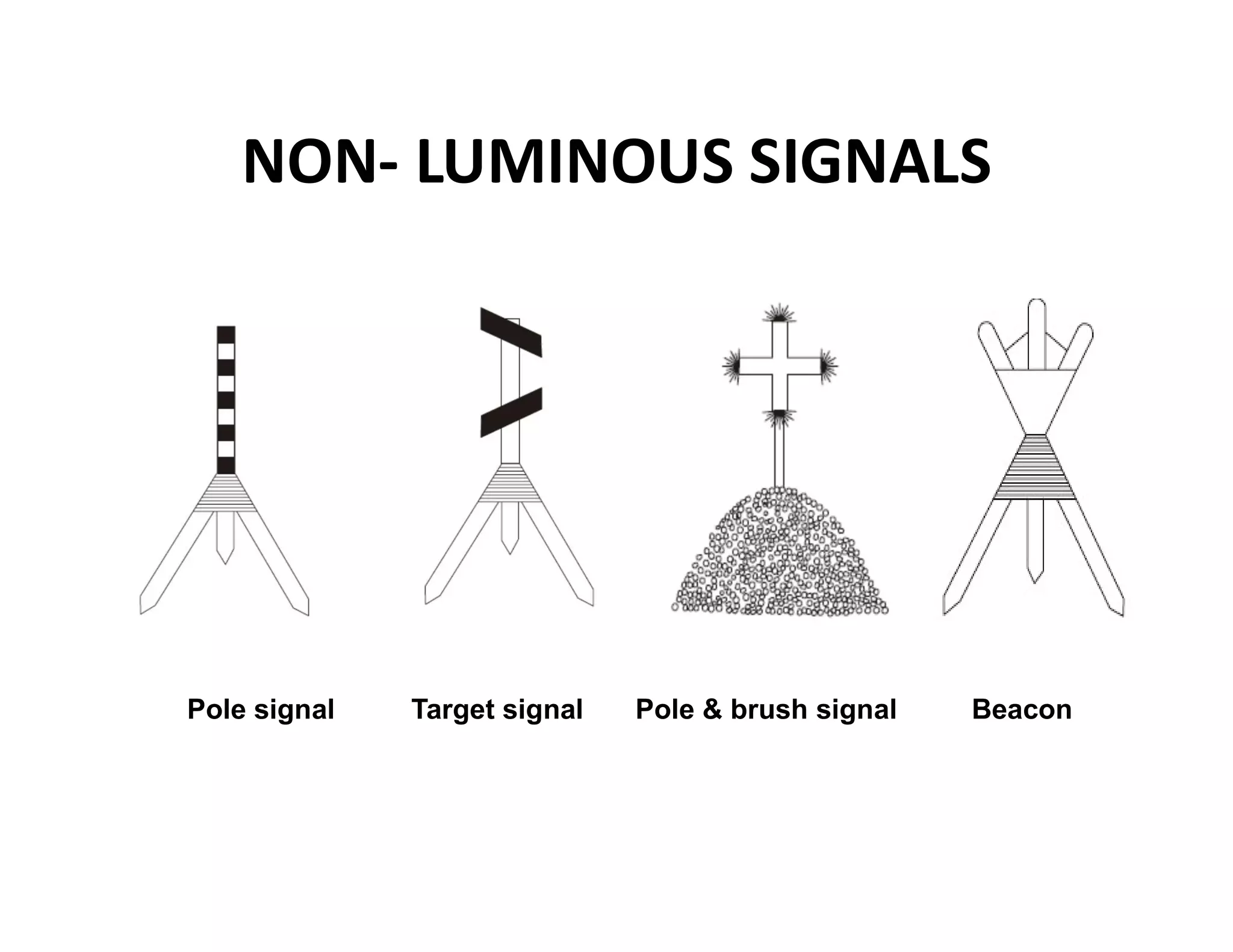
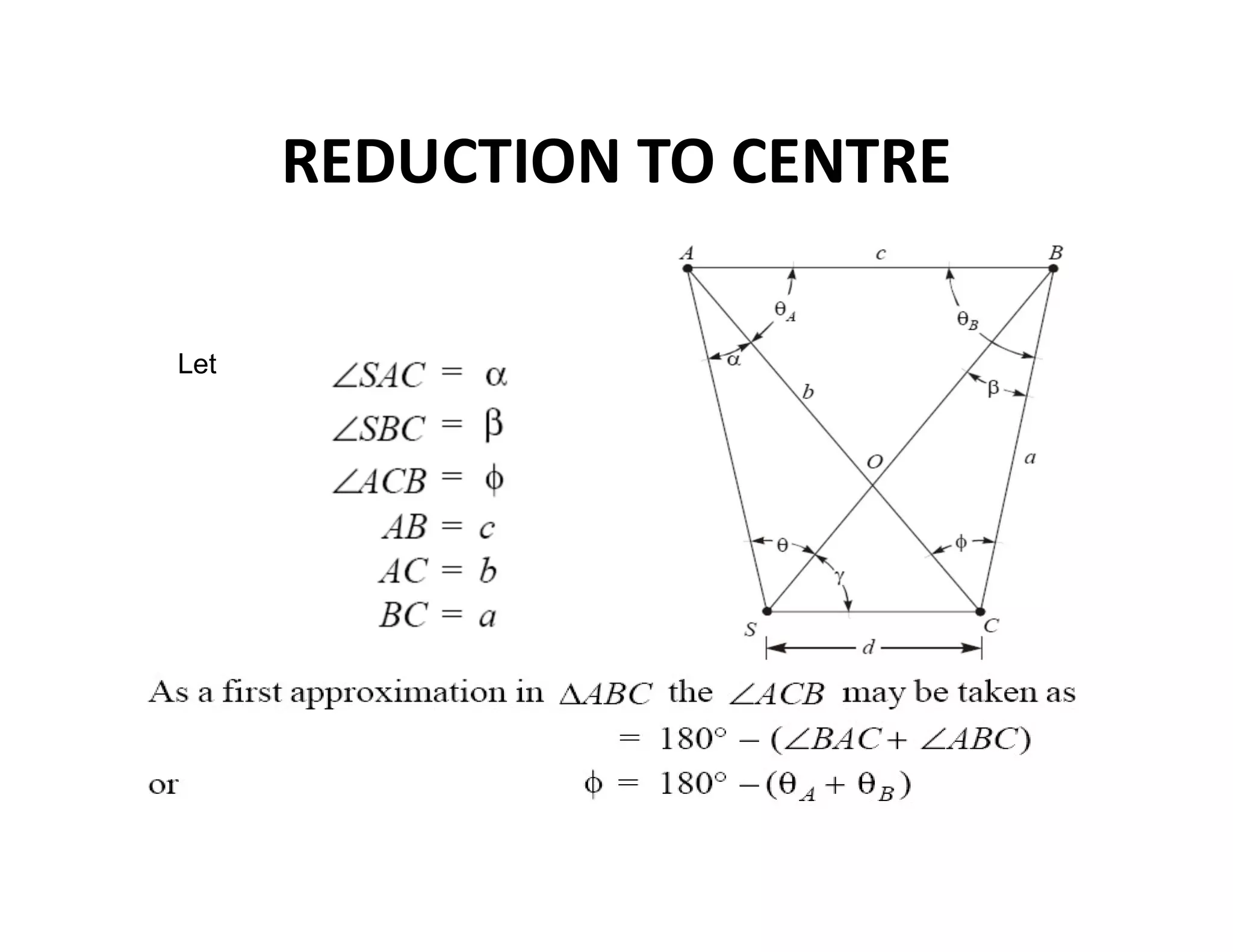
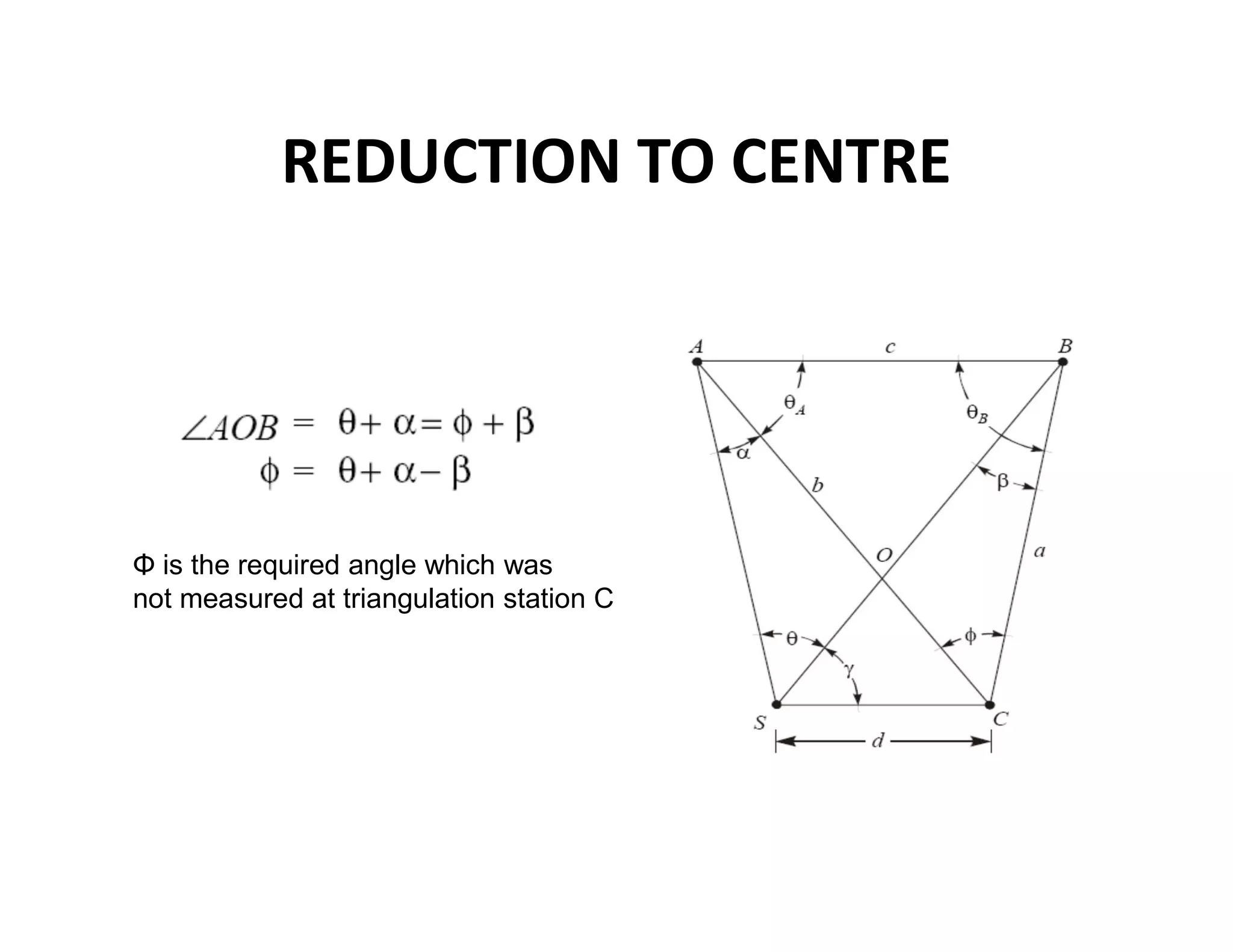
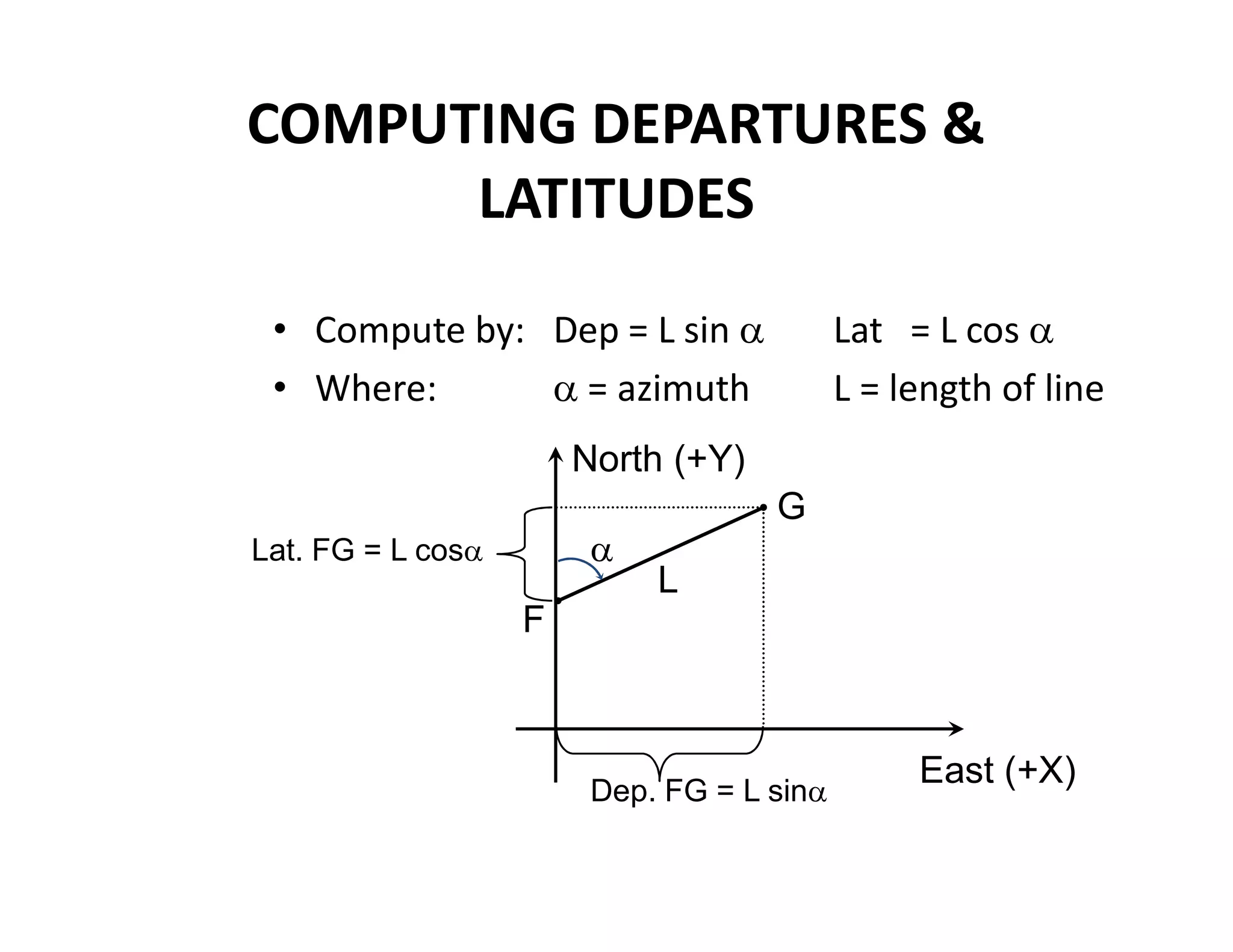
The document outlines the principles and classification of geodetic surveying and triangulation systems, detailing methodologies, types of errors, and essential formulas for establishing accurate positional measurements. It discusses the objectives of triangulation, including determining the earth's shape, providing control for surveys, and proper selection of triangulation stations and layouts. The text also emphasizes the significance of careful surveying techniques and computations required for triangulation accuracy.