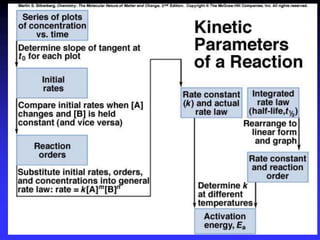
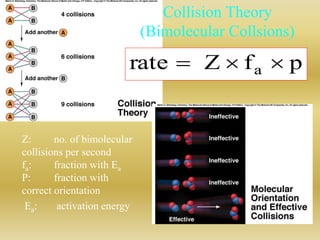
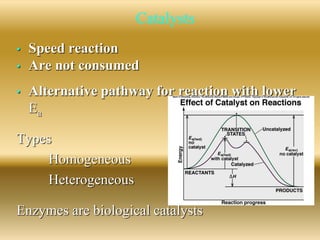
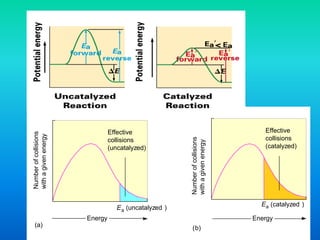
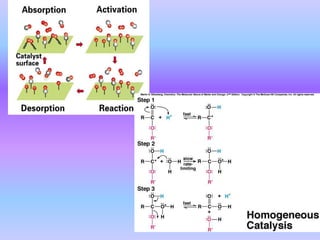
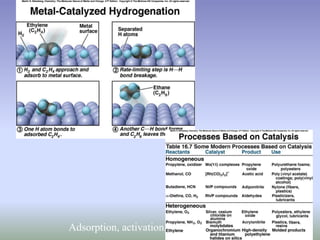
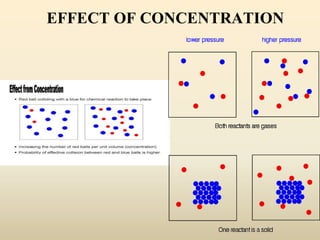
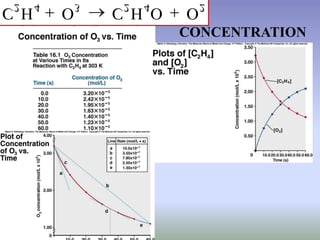
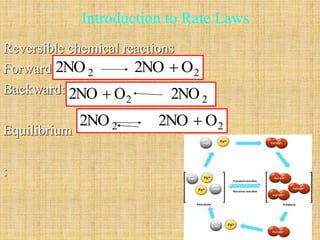
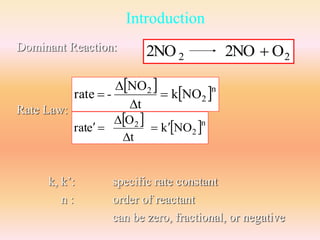
The document discusses chemical kinetics and reaction rates. It defines zero, first, and second-order reactions based on how the reaction rate depends on reactant concentrations. For zero-order reactions, the rate is independent of concentration. For first-order reactions, the rate is directly proportional to one reactant concentration. For second-order reactions, the rate is proportional to the product of two reactant concentrations or the square of one reactant concentration. It also presents the integrated rate laws and methods for determining the order of a reaction from experimental data by plotting concentrations versus time.

1. CHEMICAL
KINETICS

2. HOMOGENEOUS REACTIONS
in which all reactants and products are in one
phase
KINETICS Chemical kinetics, also known as
reaction kinetics, is the study of rates of
chemical processes

3. KINETICS
Reaction Rates
Factors affecting rate
Quantitative rate
expressions
Determination
Factors
Models for Rates
Reaction
Mechanisms
Effects of catalysts

4. RATES
B A 
Change in concentration of a reactant or
product per unit rate
. per unit volume of the fluid for fluid-phase reactions, per unit
area (or unit mass) of the
     A

t
A - A
t 0
t - t
Change in conc, A
Change in time, t
t 0


 

5. Temperature

6. Nature Of
The
Reactants
Complexity
Bond strengths
Etc.

7. STATE OF
SUBDIVISION/SURFACE
AREA

8. EFFECT OF CONCENTRATION

9. 2 4 3 2 4 2 C H  O  C H O  O
CONCENTRATION

10. Time(s) [NO2] [NO] [O2]
0 0.0100 0.0000 0.0000
50 0.0079 0.0021 0.0011
100 0.0065 0.0035 0.0018
150 0.0055 0.0045 0.0023
200 0.0048 0.0052 0.0026
250 0.0043 0.0057 0.0029
300 0.0038 0.0062 0.0031
350 0.0034 0.0066 0.0033
400 0.0031 0.0069 0.0035
2 2 2NO 2NO  O

11. Graph: Concentration vs. time
   NO  -  NO
    
2 2 400 2 0      
Concentration vs Time
0.012
0.01
0.008
0.006
0.004
0.002
0
NO
0 50 100 150 200 250 300 350 400 450
Time, sec
Conc.,mol/L
[NO2]
[NO]
[O2]
2 2 2NO 2NO  O
1.725 10 M
0.0031 - 0.0100
400 - 0
t - t
t
5
400 0


-[NO2]/t time period(s)
–4.20E-05 0 - 50
–2.80E-05 50 - 100
–2.00E-05 100 - 150
–1.40E-05 150 - 200
–1.00E-05 200 - 250
–1.00E-05 250 - 300
–8.00E-06 300 - 350
–6.00E-06 350 - 400
–1.75E-05 0 - 400 Concentration vs Time
0.012
0.01
0.008
0.006
0.004
0.002
0
0 50 100 150 200 250 300 350 400 450
Time, sec
Conc.,mol/L
[NO2]
[NO]
[O2]

12. Instantaneous rate
Slope of tangent line at a point on the graph


y
x
slope of tangent line

 NO

rate 2

t


 
0.009M
375 s
NO
rate @ 100 s 2 


t


M
s
rate @ 100 s 2.4 10 -5  

13. INSTANTANEOUS RATE
Concentration vs Time
0.012
0.01
0.008
0.006
0.004
0.002
0
0 50 100 150 200 250 300 350 400 450
Time, sec
Conc.,mol/L
[NO2]
[NO]
[O2]
12_291
0.0003
70s
O2
0.0100
0.0075
0.005
0.0025
0.0006
70s
0.0026
110 s
NO2
NO
50 100 150 200 250 300 350 400
Concentrations (mol/L)
Time (s)
[NO2 ]
 t

14. Concentration vs Time
0.012
0.01
0.008
0.006
0.004
0.002
0
0 50 100 150 200 250 300 350 400 450
Time, sec
Conc.,mol/L
[NO2]
[NO]
[O2]
 NO

rate 2

t




y
x
slope of tangent line

 
0.010M
225 s
NO
rate @ 0 s 2 


t


M
s
rate @ 0 s 4.4 10 -5  
Slope of tangent line at time
0 (y intercept)
Initial Rate (t = 0)

15. RATE LAWS
 m n rate  k A B
k = rate constant
m, n = order
2 2 2NO 2NO  O
rate = k[NO2]n
Order of Reaction In chemical kinetics, the order of
reaction with respect to a certain reactant, is defined
as the power to which its concentration term.

16. Introduction to Rate Laws
Reversible chemical reactions
Forward:
Backward:
Equilibrium
:
2 2 2NO 2NO  O
2NO O 2NO 2 2 
2 2 2NO 2NO  O

17. Introduction
Dominant Reaction:
Rate Law:
2 2 2NO 2NO  O
 
 n
2
NO
2 k NO
t

rate 

O
k, k’: specific rate constant
n : order of reactant
can be zero, fractional, or negative
 -
 
 n
2
2 k NO
t
rate  


 

18. Method of Initial Rates
 m n rate  k A B
Unknown: k, m, n
Initial rate: instantaneous rate just after
reaction is initiated

19. Initial Rates, NO2 decomposition
2 2 2NO 2NO  O

 -
rate 
Experiment
 NO

2 k NO
t

Initial Conc.
[NO2]
 n
2
Rate [O2]
Formation
1 0.01 7.1 x 10-5
2 0.02 2.8 x 10-4

20. General:
- k NO
rate 2
Substituting:
Solution:
n
 
2 2
 n
1 2
- k NO
rate 1

n
 
 n
1
- k 0.020
2
-4
2.8 10
-5
- k 0.010

7.1 10


4  (2) n
so n 
2 ln 4 
n ln 2

21. Rate constant
Rate 1
 
 n
2
NO
2 k NO
t

 -
rate 

7.1 x 10-5 M s-1 = -k[0.01 M]2
k = 0.71 M-1 s-1
Rate 2
2.8 x 10-4 M s-1 = -k[0.02 M]2
k = 0.70 M-1 s-1
 
 2
2
NO
2 0.70 NO
t
rate law  




22. Experiment
H I 2HI 2 2  
Initial Conc.
[H2]
Initial Conc.
[I2] Rate
1 0.0113 0.0011 1.9 x 10-23
2 0.0220 0.0033 1.1 x 10-22
3 0.0550 0.0011 9.3 x 10-23
4 0.0220 0.0056 1.9 x 10-22

23. O2 + 2 NO  2NO2

24. Types
Differential:
Rate dependence on concentration

 -
rate 

rate  
Integrated:
 
 n
2
NO
2 k NO
t

 
 n
2
O
2 k NO
t

 
Concentration dependence on time

25. First Order Reactions
For aA  products
Differential:
 
kA
A

 -
rate 

t
   0 ln A  - kt  ln A t
Integrated: first order reaction (order = 1) has a
rate proportional to the concentration of one of
the reactants. A common example of a first-order
reaction is the phenomenon of  A
radioactive 
0 decay.
The rate law is:
ln 
kt
 A

rate = k[A] (or B instead of A), with t
k having the
The rate of reaction is proportional to the
concentration of A

26. Half-life, first order reactions
Integrated law:
Half-life:
Half of initial reacted
[A]t = ½[A]0
Independent of [A]0
 
 
kt
A
ln 0 
A
t
ln2
0.693
k
t
k
t
2
1
2
1



27. First order
Plot:
ln[A] vs. time
ln[A]
ln[A]0
slope = -k
time
lnA  - kt  lnA0 t
y mx  b

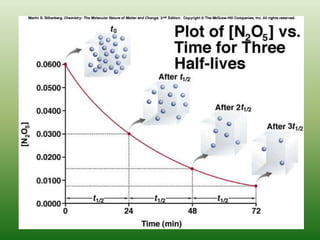
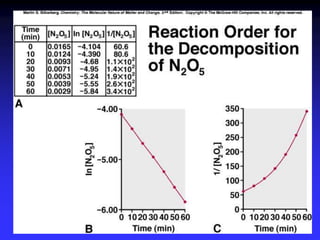
30. SECOND-ORDER REACTION
A second-order reaction (order = 2) has a rate
proportional to the concentration of the square
of a single reactant or the product of the
concentration of two reactants:
rate = k[A]2 (or substitute B for A or k multiplied
by the concentration of A times the
concentration of B), with the units of the rate
constant M-1sec-1

31. SECOND ORDER
1
kt
1
   0 A
Plot:
1 vs. time
[A]
1
[A]o
slope = k
time
y mx  b
A
 
t
1
[A]

32. SECOND ORDER REACTIONS
For aA  products
Differential:
Integrated:
 
kA2
A
rate 

t

 -
1
   0 A
1
1
 
   
kt
A
A
0
t
1
kt
A
 
t

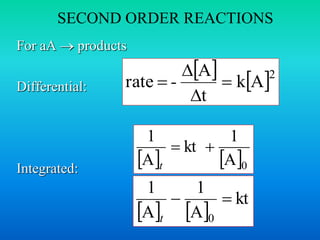
33. HALF-LIFE, SECOND ORDER
REACTIONS
Integrated law:
Half-life:
Half of initial reacted
[A]t = ½[A]0
1
1
 
   
Inversely proportional to [A]0
kt
A
A
0
t
1
 0 k A
t
2
1


34. Zero-order reactions (order = 0) have a constant
rate. This rate is independent of the
concentration of the reactants. The rate law is:
rate = k, with k having the units of M/sec.

35. Zero Order Reactions
For aA  products
Differential:
Integrated:
 
rate 0  
kA k
A

t

 -
   0 A  - kt  A t
A A - kt 0   t

36. Zero order
   0 A  - kt  A t
Plot:
[A] vs. time
[A]
[A]0
slope = -k
time
y mx  b

38. Graphical Method
First order
Second order
Zero order
Straight line
lnA  - kt  lnA0 t
1
kt
1
 A
  A
0  
t
   0 A  - kt  A t
y  mx  b

41. Summary
Conditions set so dominant forward reaction
Differential Rate Laws
rate as a function of concentration
method of initial rates
Integrated Rate Laws
concentration as a function of time
graphical method
Experimental data collection
Rate law types can be interconverted

42. Reaction Mechanism
Chemical equation: Summary
Mechanism: Series of elementary steps
Elementary Steps: Reactions with rate laws
from molecularity
Molecularity: Number of species that must
collide to produce reaction

44. Reaction Mechanism
Proposed elementary steps must satisfy conditions:
— reasonable reactions
— sum of steps = overall balanced reaction
— mechanism rate law = experimental rate law

45. Intermediates
—appear in steps
—produced in one step
—used in subsequent
—not in overall equation

46. Rate-determining step
In a multi-step process:
SLOWEST step
Determines overall reaction rate
“Bottleneck”

47. Model for Kinetics
Collision Theory
rate determined by particle collisions
collision frequency and energy
Cl + NOCl → Cl2 + NO
Transition State Theory
how reactants convert to products

50. rate Z f p a   
Z: no. of bimolecular
collisions per second
fa: fraction with Ea
P: fraction with
correct orientation
Ea: activation energy
Collision Theory
(Bimolecular Collsions)

52. Arrhenius Equation
Ea
RT
k Ae


k: rate constant
Ea: activation energy (minimum required)
T: absolute temperature
R: universal gas constant
A: orientation factor
Energy & orientation requirements for reaction

53. Hydrolysis of an ester

55. Transition State Theory
Ea and internal energy:
Bonds breaking and forming
Atoms rearranging
“Transition State”
Unstable intermediate
At point of highest energy

56. forward reaction reverse reaction

58. I- + CH3Cl  Cl- + CH3I

61. Catalysts
• Speed reaction
• Are not consumed
• Alternative pathway for reaction with lower
Ea
Types
Homogeneous
Heterogeneous
Enzymes are biological catalysts

62. 12_304
Effective
collisions
(uncatalyzed)
Ea (uncatalyzed )
Effective
collisions
(catalyzed)
Ea (catalyzed )
Number of collisions
with a given energy
Number of collisions
with a given energy
Energy Energy
(a) (b)

64. Adsorption, activation, reaction, desorption