The document discusses chemical kinetics, which is the study of reaction rates and mechanisms. It covers key topics such as:
- Reaction rates can be defined as the change in concentration of reactants or products over time.
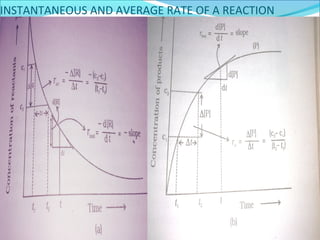
- Instantaneous and average reaction rates, where instantaneous rate is preferable since rate changes over time.
- Rate laws express the reaction rate in terms of molar concentrations of reactants, with order of the reaction being the sum of exponents.
- Reaction orders can be determined experimentally and differ from stoichiometric coefficients. Integrated rate equations take different forms depending on the reaction order.
- Methods for determining the order of a reaction include differential, isolation, integration, and half-life
![CHEMICAL KINETICS
The study of reaction rates and their mechanisms is called chemical
kinetics. The word kinetics means movement.Thermodynamics tell
about the feasibility of a reaction(∆G = −ve).Which product is stable(at
equilibrium)? Where as Kinetics tell about the (rate) of a chemical
process and mechanism of a reaction(any intermediate).
Thermodynamics favors the process (∆G: -ve ) .Kinetics makes this
reaction nearly impossible (Requires a very high pressure and
temperature over long time. Chemical kinetics also known as Reaction
kinetics is the study of rate of chemical processes.
Rate of a Chemical Reaction: The speed of a reaction or the rate of a reaction
can be defined as the change in concentration of a reactant or product in unit
time. Consider a reaction ,R P,If [R]1 and [p]1 are the concentration of
reactant and product at time T1 and [R]2 and [p]2 are the concentration of reactant
and product at time T2 , ∆t= T2 -T1 and Δ [R] = [R]2 - [R]1 and Δ [p] = [p]2 - [p]1
Rate of disappearance R = -Change in concentration(∆R)= +Change in
concentration(∆P)
time (∆t) time (∆t)](https://image.slidesharecdn.com/ldskinetics-3-170828154531/75/Lds-kinetics-3-1-2048.jpg)
![Unit of rate of a reaction :-
unit of rate of a reaction are concentration time-1
.If concentration is
in mol L-1
S-1
. In gases reactions the unit of a rate equation will be
atm S-1
.
Rate can be expressed in three different ways;
(i) Initial rate: rate of reaction in the starting time is initial rate.
(ii) Average rate:- Average rate is the rate of a reaction which
measure at a particualr period of time interval. Average rate cannot
be used to predict the rate of a reaction at a particular instant as it
would be constant for the time interval for which it is calculated. So
to express the rate at a particular moment of time we used
instantaneous rate.
rav= -Δ[R] = Δ[P]
Δt Δt
(iii)Instantaneous rate: The rate at a particular moment of time is
instantaneous rate. As Δt →0 or rinst= -d[R] = d[P]
dt dt](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-3-320.jpg)
![Rate changes with time hence expressing the rate as an instantaneous
rate is preferable.
Instantaneous rate means rate at a particular instant (infinitesimal change
in time) i.e. Rate = ± d[concentration]
dt
For the reaction,
5Br-
(aq) +BrO3
-
(aq) +6H+
(aq) 3Br→ 2(aq) +3H2O
Rate= -1Δ[Br-
] = -1 Δ[Br O3
-
] = -1 Δ[H+
] = 1 Δ[Br2]= 1 Δ [H2O]
5 Δt Δt 6 Δt 3 Δt 3 Δt
Concentration
Time](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-4-320.jpg)
![Rate Law Expression and rate constant:
The rate of a chemical reaction at a given temperature depends on
concentration,(pressure in gases), temperature , catalyst. The representation of
rate in terms of concentration of reactants is called as rate law.
The rate of a homogeneous reaction is proportional to the
product of the concentrations of the reactants raised to some
power.
Thus for a general reaction
or -d[R] =k[A]x
[B]Y
dt
This equation is known as differential equation and k is called
rate constant or specific rate or velocity constant. It is
independent of concentrations and time.Has a specific value at
a given temperature .
or](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-5-320.jpg)

![ The sum of the powers of the concentration terms (α + β)
in the rate equation is known as the overall order of the
reaction.
α, β are called the partial orders w. r. t the reactants A
and B respectively.
The order of a reaction generally has a value 0 to 3
Order can also have fractional value e.g. decomposition
of acetaldehyde: CH3CHO → CH4 + CO, rate = k
[CH3CHO]3/2
order = 3/2 or 1.5
Order is different from the stoichiometric coefficient and
needs to be determined experimentally.
Order of a Reaction](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-7-320.jpg)
![Reaction Orders and Rate
The reaction order, n, determines how the rate depends on
the concentration of the reactant.
The rate law for the
reaction can be written:
Rate = k[A]0
= k
Rate = k[A]1
Rate = k[A]2](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-8-320.jpg)
![Unit of Rate of Reaction
Concentration time−1
e.g. mol L−1
sec−1
or mol dm−3
sec−1
Gaseous reactions: Pressure time−1
e.g. torr sec−1
(1)For a 0th
order reaction: Rate = k
k = rate = [conc.] time−1
= mol L−1
sec−1
(2)For a 1st
order reaction: Rate = k [conc.]
k = rate/[conc.] = [conc.] time−1
/[conc.] = time−1
= sec−1
(3)For a 2nd
order reaction: Rate = k [conc.]2
k = rate/[conc.]2
= [conc.] time−1
/[conc.]2
= [conc.]−1
time−1
= mol −1
L
sec−1
(4)For a nth
order reaction: Rate = k [conc.]n
k = rate/[conc.]n
= [conc.] time−1
/[conc.]n
= [conc.]1−n
time−1
since ,thus K=rate/[A]x
[B]y
=concentration x 1
time ( concentration )n](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-9-320.jpg)

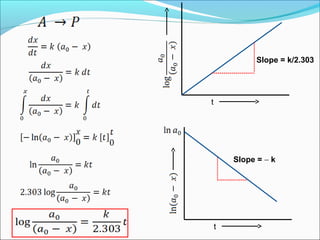
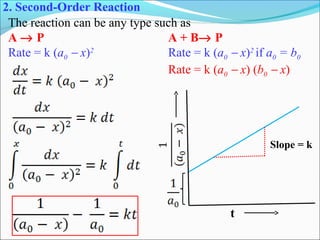
![Integrated rate equation: It is different for different order reaction
(1)Zero Order reactions: For a zero order reaction R P
Rate= -d[R] /dt = K[R]0
As any quantity raised to power zero is 1
Thus rate= -d[R] /dt = Kx1.
Rearrange the equation, d[R] = - kdt
Integrating both side , [R] = - kt + I………(.1)
At t=0,R=[R]0
Substituting in equation , [R]0
= - Kx0+I, [R]0
=I
Substituting the value of I in the equation. [R] = - Kt+[R]0
………..(2)
If we plot [R] against t, we get a straight line with slope = -K and intercept
equal to [R]0
simplifying equation . we get the rate constant k= [R]0
- [R]
t
[R]
K= - Slope
Concentration R](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-11-320.jpg)
![1st
order reactions:-
For a reaction R → P
Rate=-d[R] /dt = K[R]
Or d[R] = -kdt
[R]
Integrating the equation ln[R] =-kt+I…………….(1)
When t=0,R=[R]0 where [R]0 is the initial concentration of the reactant.
Then , ln[R]0 =-kx0+I
ln[R]0 =I
Substituting “I “in equation 1, we get, ln[R] =-kt+ ln[R]0
Rearranging the equation ln [R] = -kt
[R]0
Or k= 1 ln [R]
T [R]0
At time t1, ln[R]1 =-kt1+ ln[R]0 ……………………(2)
At time t2 , ln[R]2 =-kt2+ ln[R]0 ………………………(3)
Substracting 3 from 2 we get,ln[R]1- ln[R]2=-kt1 –( -kt2)
or ln [R]1 = k(t2-t1)
[R]2
Thus K= 1 ln [R] ………………….(4)](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-12-320.jpg)
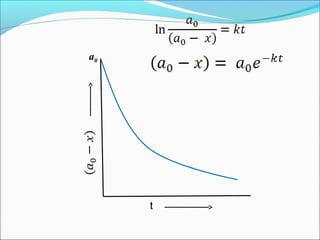
![The equation ln[R] =-kt+ ln[R]0 can be written as
ln [R] = - kt
[R]0
Taking anti log in both sides [R]= [R]0 e-kt
The equation ln[R] =-kt+ ln[R]0 is like y=mx+C .
If we plot [R] against t we get a straight line with
slope =–k and intercept =ln[R]0
Thus first order reaction can be written as
K=2.303 log [R]0
t [R]
This is the formula of rate constant for first order
reaction](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-13-320.jpg)
![(1)Plot [R] against t and( 2) ln [R] vs t for 1st
order reaction
[R]0
ln[R]0 ln[R]0
ln [R] k=-slope [R] slope=k/2.303
↑ ↑
t→ t→](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-14-320.jpg)

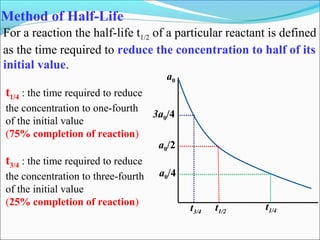
![HALF LIFE PERIOD:It is the time in which the concentration of a
reactant is reduced to one half of its initial concentration .
For zero order reaction. K= [R]0
- [R]
t
At t=t1/2 , [R] = 1[R]0
2
The rate constant at t1/2 becomes k= [R]0
-1/2[R]0
t1/2 thus , t1/2 == [R]0
2k
For 1st order reaction.:-K=2.303 log [R]0
t [R]
At t=t1/2 , [R] = [R]0
2
Thus, K=2.303 log [R]0
t1/2 [R]/2
t1/2 =2.303 log2
k
t1/2 =2.303 x 0.301 Thus, t1/2 =0.693
k k](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-16-320.jpg)
![Pseudo 1st
order reaction:
when 2 reactant react out of which 1 is in large excess than the other
and behave as 1st
order then it is called as pseudo 1st
order reaction.
Eg ,
CH3COOC2H5 + H2O → CH3COOH + C2H5OH
T=0, 0.01mol 10 mol 0mol 0mol
At t 0 mol 9.9mol 0.01mol 0.01mol
Rate =K’[CH3COOC2H5 ] [H2O]
Where k= K’[H2O]
The reaction behave as 1st
order reaction and called as pseudo order
reactions.](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-17-320.jpg)



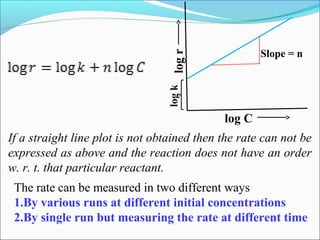
![1. With different initial concentrations
Various runs are carried out at different initial concentrations
of the reactant and initial rates are measured by measuring the
initial slopes.
[C]
r1
t
r2
r3
r4
logr
log C
logk
Slope = nC
r1
r2
r3
r4
This procedure avoids the possible complications due to the
interference by products (e.g. inhibition or autocatalysis)
The order thus determined is called order w.r.t. conc. or true
order (nC)](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-22-320.jpg)
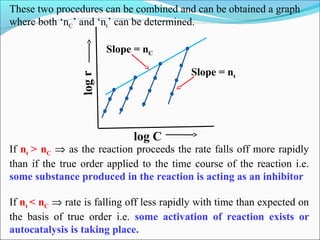
![2. At different time
In this procedure a single run is carried out and the slopes are
measured at different times. So this gives variation of rate
with respect to time.
logr
log C
logk
Slope = nt
r1
r2
r3
r4
Time
[C]
r1
r2
r3
r4
The order thus determined is called order w.r.t. time (nt)](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-23-320.jpg)

![2. Isolation Method
If all the reactants except one are present in excess, the
apparent order will be the order w.r.t. the one “isolated”
reactant.
If a reaction rate is expressed as: Rate = k [A]α
[B]β
[C]γ
B and C are taken in excess of A and the order w.r.t A is
determined which will be ‘α’.
The order w.r.t. B and C can also be determined by similar
procedure.
This method is often used in conjunction with other
methods.
Sometimes taking a large excess of concentration of a
particular reactant may change the mechanism of a
composite reaction.](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-26-320.jpg)


![Let’s consider the reaction
A → P
Rate = k (constant)
3. Zero-Order Reaction
t
Slope = − k
[A]
[A]0
Rate
[A]](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-32-320.jpg)




![For a Zero order reaction
At t = t1/2 [A] = [A]0/2
kt1/2 = [A]0 – [A]0/2
t1/2 = [A]0/2k
t1/2 ∝ [A]0
For a zero order reaction the half-life is directly
proportional to the initial concentration of the
reactant.](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-38-320.jpg)






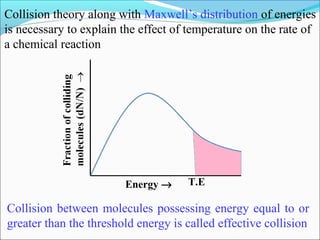
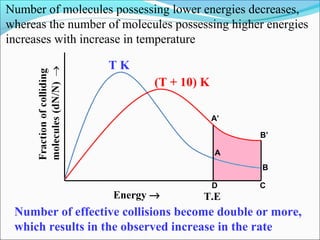
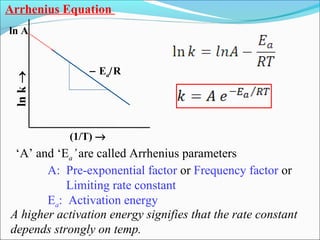
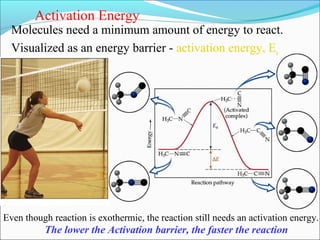







![The rate expressed in moles/unit volume/unit time is
If the reaction is first order w.r.t. both A and B
A + B → P
r = k [A] [B]](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-61-320.jpg)


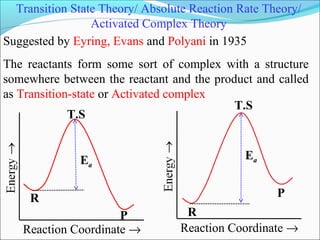

![Let’s consider a simple bimolecular reaction
K#
k#
Rate of the reaction = k#
[AB#
]
The rate constant (k#
) is related to the vib. frequency (ν) as
k#
= κ ν where κ = kappa = transmission coeff. and 0 < κ ≤ 1
In AB#
one of the vib. degree of freedom = translational degree of
freedom which is responsible for the product formation
The rate at which the activated complex moves across the energy
barrier is proportional to the vibrational frequency ‘ν’
For convenience the value of κ is taken = 1 and we know kBT = hν](https://image.slidesharecdn.com/ldskinetics-3-170828154531/85/Lds-kinetics-3-66-320.jpg)


