The document discusses chemical kinetics, focusing on the rate and order of reactions, describing rate laws based on experimentally derived equations relating reaction rates to reactant concentrations. It explains the determination of rate equations through initial rate and graphical methods and provides examples to illustrate the concepts, including various order reactions. Overall, it serves as a comprehensive guide for understanding and calculating reaction rates in chemical processes.

1. 1
CHEMICAL KINETICS
A.K.GUPTA, PGT CHEMISTRY,
KVS ZIET BHUBANESWAR
A.K.GUPTA
PGT CHEMISTRY
KVS ZIET BHUBANESWAR

2. 2
Rate and OrderRate and Order
of Reactionsof Reactions
A.K.GUPTA, PGT CHEMISTRY, KVS ZIET BHUBANESWAR

3. 3
For the reaction aA + bB → cC + dD
Rate = k[A]n
[B]m
Rate law or rate equation:
Experimentally derived algebraic
equation which relates the rate of
reaction with the concentration of
the reactants
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

4. 4
For the reaction aA + bB → cC + dD
Rate = k[A]n
[B]m
where n and m are the orders of reaction
with respect to A and B
n and m can be ± integers or fractional
n + m is the overall order of reaction.
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

5. 5
For the reaction aA + bB → cC + dD
Rate = k[A]n
[B]m
For multi-step reactions, n & y have no direct
relation to the stoichiometric coefficients and
can ONLY be determined experimentally.
For single-step reactions (elementary
reactions),
n = a and m= b
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

6. 6
For the reaction aA + bB → cC + dD
Rate = k[A]n
[B]m
n = 0 → zero order w.r.t. A
n = 1 → first order w.r.t. A
n = 2 → second order w.r.t. A
m = 0 → zero order w.r.t. B
m = 1 → first order w.r.t. B
m = 2 → second order w.r.t. B
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

7. 7
For the reaction aA + bB → cC + dD
Rate = k[B]2
Describe the reaction with the following rate law.
The reaction is zero order w.r.t. A and
second order w.r.t. B.
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

8. 8
Rate = k[A]n
[B]m
Where k is the rate constant
(specific rate) of the reaction
For the reaction aA + bB → cC + dD
• Temperature-dependent
• Can only be determined from experiments
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR
k is

9. 9
Rate = k[A]n
[B]m
units of k : -
mol L−1
s−1
/(mol L−1
)n+m
or,
mol L−1
min−1
/(mol L−1
)n+m
For the reaction aA + bB → cC + dD
m1n1
11
mn
)L(mol)L(mol
sLmol
[B][A]
rate
k −−
−−
==
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

10. 10
Rate = k[A]0
[B]0
units of k
= mol L−1
s−1
/(mol L−1
)0+0
= mol L−1
s−1
= units of rate
For the reaction aA + bB → cC + dD
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

11. 11
Rate = k[A][B]0
units of k
= mol L−1
s−1
/(mol L−1
)1+0
= s−1
For the reaction aA + bB → cC + dD
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

12. 12
Rate = k[A][B]
units of k
= mol L−1
s−1
/(mol L−1
)1+1
= mol−1
L1
s−1
For the reaction aA + bB → cC + dD
The overall order of reaction can be
deduced from the units of k
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

13. 13
Rate = k[A]n
[B]m
[C]p
…
For the reaction
aA + bB + cC + … → products
units of k : -
mol L−1
s−1
/(mol L−1
)n+m+p+…
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

14. 14
Determination of rate equations
To determine a rate equation is to find n, m, p,
z,…
Rate = k[A]n
[B]m
[C]p
…
Two approaches : -
1. Initial rate method
2. Graphical method
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

15. 15
Determination ofDetermination of
Rate LawRate Law
byby
Initial Rate MethodsInitial Rate Methods
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

16. 16
5Cl−
(aq) + ClO3
−
(aq) + 6H+
(aq) → 3Cl2(aq) + 3H2O(l)
Expt
[Cl−
(aq)]
(mol L−1
)
[ClO3
−
(aq)]
(mol L−1
)
[H+
(aq)]
(mol L−1
)
Initial rate
(mol L−1
s−1
)
1 0.15 0.08 0.20 1.0×10−5
2 0.15 0.08 0.40 4.0×10−5
3 0.15 0.16 0.40 8.0×10−5
4 0.30 0.08 0.20 2.0×10−5
Suppose the rate law for the reaction is
rate = k[Cl−
(aq)]n
[ClO3
−
(aq)]m
[H+
(aq)]p
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

17. 17
Expt
[Cl−
(aq)]
(mol L−1
)
[ClO3
−
(aq)]
(mol L−1
)
[H+
(aq)]
(mol L−1
)
Initial rate
(mol L−1
s−1
)
1 0.15 0.08 0.20 1.0×10−5
2 0.15 0.08 0.40 4.0×10−5
3 0.15 0.16 0.40 8.0×10−5
4 0.30 0.08 0.20 2.0×10−5
pmn
pmn
5
5
(0.20)(0.08)(0.15)
(0.40)(0.08)(0.15)
101.0
104.0
=
×
×
−
−
From experiments 1 and 2,
4 = 2p
⇒ p = 2
= 2p
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

18. 18
Expt
[Cl−
(aq)]
(mol L−1
)
[ClO3
−
(aq)]
(mol L−1
)
[H+
(aq)]
(mol L−1
)
Initial rate
(mol L−1
s−1
)
1 0.15 0.08 0.20 1.0×10−5
2 0.15 0.08 0.40 4.0×10−5
3 0.15 0.16 0.40 8.0×10−5
4 0.30 0.08 0.20 2.0×10−5
pmn
pmn
5
5
(0.40)(0.08)(0.15)
(0.40)(0.16)(0.15)
104.0
108.0
=
×
×
−
−
From experiments 2 and 3,
2 = 2m
⇒ m = 1
= 2m
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

19. 19
Expt
[Cl−
(aq)]
(mol L−1
)
[ClO3
−
(aq)]
(mol L−1
)
[H+
(aq)]
(mol L−1
)
Initial rate
(mol L−1
s−1
)
1 0.15 0.08 0.20 1.0×10−5
2 0.15 0.08 0.40 4.0×10−5
3 0.15 0.16 0.40 8.0×10−5
4 0.30 0.08 0.20 2.0×10−5
pmn
pmn
5
5
(0.20)(0.08)(0.15)
(0.20)(0.08)(0.30)
101.0
102.0
=
×
×
−
−
From experiments 1 and 4,
2 = 2n
⇒ n = 1
= 2n
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

20. 20
rate = k[Cl−
(aq)][ClO3
−
(aq)][H+
(aq)]2
Expt
[Cl−
(aq)]
(mol L−1
)
[ClO3
−
(aq)]
(mol L−1
)
[H+
(aq)]
(mol L−1
)
Initial rate
(mol L−1
s−1
)
1 0.15 0.08 0.20 1.0×10−5
2 0.15 0.08 0.40 4.0×10−5
3 0.15 0.16 0.40 8.0×10−5
4 0.30 0.08 0.20 2.0×10−5
From experiment 1,
1.0×10−5
= k(0.15)(0.08)(0.20)2
k = 0.02 mol−3
L3
s−1
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

21. 21
rate = k[Cl−
(aq)][ClO3
−
(aq)][H+
(aq)]2
Expt
[Cl−
(aq)]
(mol L−1
)
[ClO3
−
(aq)]
(mol L−1
)
[H+
(aq)]
(mol L−1
)
Initial rate
(mol L−1
s−1
)
1 0.15 0.08 0.20 1.0×10−5
2 0.15 0.08 0.40 4.0×10−5
3 0.15 0.16 0.40 8.0×10−5
4 0.30 0.08 0.20 2.0×10−5
From experiment 2,
4.0×10−5
= k(0.15)(0.08)(0.40)2
k = 0.02 mol−3
L3
s−1
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

22. 22
Question 2C + 3D + E → P + 2Q
Exp.
[C]
( mol L−1
)
[D]
( mol L−1
)
[E]
( mol L−1
)
Initial rate
( mol L−1
s-1
)
1 0.10 0.10 0.10 3.0×10−3
2 0.20 0.10 0.10 2.4×10−2
3 0.10 0.20 0.10 3.0×10−3
4 0.10 0.10 0.30 2.7×10−2
(a) rate = k[C]n
[D]m
[E]p
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

23. 23
Exp.
[C]
( mol L−1
)
[D]
( mol L−1
)
[E]
( mol L−1
)
Initial rate
( mol L−1
s-1
)
1 0.10 0.10 0.10 3.0×10−3
2 0.20 0.10 0.10 2.4×10−2
3 0.10 0.20 0.10 3.0×10−3
4 0.10 0.10 0.30 2.7×10−2
(a) rate = k[C]n
[D]m
[E]p
pmn
pmn
3
-2
(0.10)(0.10)(0.10)
(0.10)(0.10)(0.20)
103.0
102.4
=
×
×
−
From experiments 1 and 2,
8 = 2n
⇒ n = 3
= 2n
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

24. 24
Exp.
[C]
( mol L−1
)
[D]
( mol L−1
)
[E]
( mol L−1
)
Initial rate
( mol L−1
s-1
)
1 0.10 0.10 0.10 3.0×10−3
2 0.20 0.10 0.10 2.4×10−2
3 0.10 0.20 0.10 3.0×10−3
4 0.10 0.10 0.30 2.7×10−2
(a) rate = k[C]n
[D]m
[E]p
pmn
pmn
3
-3
(0.10)(0.10)(0.10)
(0.10)(0.20)(0.10)
103.0
103.0
=
×
×
−
From experiments 1 and 3,
1 = 2m
⇒ m = 0
= 2m
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

25. 25
Exp.
[C]
( mol L−1
)
[D]
( mol L−1
)
[E]
( mol L−1
)
Initial rate
( mol L−1
s-1
)
1 0.10 0.10 0.10 3.0×10−3
2 0.20 0.10 0.10 2.4×10−2
3 0.10 0.20 0.10 3.0×10−3
4 0.10 0.10 0.30 2.7×10−2
(a) rate = k[C]x
[D]y
[E]z
pmn
pmn
3
-2
(0.10)(0.10)(0.10)
(0.30)(0.10)(0.10)
103.0
102.7
=
×
×
−
From experiments 1 and 4,
9 = 3p ⇒ p = 2
= 3p
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

26. 26
Exp.
[C]
( mol L−1
)
[D]
( mol L−1
)
[E]
( mol L−1
)
Initial rate
( mol L−1
s-1
)
1 0.10 0.10 0.10 3.0×10−3
2 0.20 0.10 0.10 2.4×10−2
3 0.10 0.20 0.10 3.0×10−3
4 0.10 0.10 0.30 2.7×10−2
(a) rate = k[C]3
[D]0
[E]2
= k[C]3
[E]2
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

27. 27
Exp.
[C]
( mol L−1
)
[D]
( mol L−1
)
[E]
( mol L−1
)
Initial rate
( mol L−1
s-1
)
1 0.10 0.10 0.10 3.0×10−3
2 0.20 0.10 0.10 2.4×10−2
3 0.10 0.20 0.10 3.0×10−3
4 0.10 0.10 0.30 2.7×10−2
(b) rate = k[C]3
[E]2
From experiment 1,
3.0×10−3
= k(0.10)3
(0.10)2
k = 300 mol−4
L4
s−1
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

28. 28
Question
H+
CH3COCH3(aq) + I2(aq) CH3COCH2I(aq) + H+
(aq) + I−
(aq)
Initial rate
(mol L−1
s−1
)
Initial concentration
(mol L−1
)
[I2
(aq)] [CH3
COCH3
(aq)] [H+
(aq)]
3.5 ×10−5
2.5×10−4
2.0×10−1
5.0×10−3
3.5 ×10−5
1.5×10−4
2.0×10−1
5.0×10−3
1.4 ×10−4
2.5×10−4
4.0×10−1
1.0×10−2
7.0 ×10−5
2.5×10−4
4.0×10−1
5.0×10−3
(a) Suppose,
rate = k[I2(aq)]n
[CH3COCH3(aq)]m
[H+
(aq)]p
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

29. 29
Initial rate
(mol L−1
s−1
)
Initial concentration
(mol L−1
)
[I2
(aq)] [CH3
COCH3
(aq)] [H+
(aq)]
3.5 ×10−5
2.5×10−4
2.0×10−1
5.0×10−3
3.5 ×10−5
1.5×10−4
2.0×10−1
5.0×10−3
1.4 ×10−4
2.5×10−4
4.0×10−1
1.0×10−2
7.0 ×10−5
2.5×10−4
4.0×10−1
5.0×10−3
(a) rate = k[I2(aq)]n
[CH3COCH3(aq)]m
[H+
(aq)]p
p3-m1-n4-
p-3m-1n-4
5
-5
)10(5.0)10(2.0)10(1.5
)10(5.0)10(2.0)10(2.5
103.5
103.5
×××
×××
=
×
×
−
From experiments 1 and 2,
1 = 1.67n ⇒ n = 0
= 1.67n
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

30. 30
Initial rate
(mol L−1
s−1
)
Initial concentration
(mol L−1
)
[I2
(aq)] [CH3
COCH3
(aq)] [H+
(aq)]
3.5 ×10−5
2.5×10−4
2.0×10−1
5.0×10−3
3.5 ×10−5
1.5×10−4
2.0×10−1
5.0×10−3
1.4 ×10−4
2.5×10−4
4.0×10−1
1.0×10−2
7.0 ×10−5
2.5×10−4
4.0×10−1
5.0×10−3
(a) rate = k[I2(aq)]n
[CH3COCH3(aq)]m
[H+
(aq)]p
p3-m1-n4-
p-3m-1n-4
5
-5
)10(5.0)10(2.0)10(2.5
)10(5.0)10(4.0)10(2.5
103.5
107.0
×××
×××
=
×
×
−
From experiments 1 and 4,
2 = 2m ⇒m= 1
= 2m
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

31. 31
Initial rate
(mol L−1
s−1
)
Initial concentration
(mol L−1
)
[I2
(aq)] [CH3
COCH3
(aq)] [H+
(aq)]
3.5 ×10−5
2.5×10−4
2.0×10−1
5.0×10−3
3.5 ×10−5
1.5×10−4
2.0×10−1
5.0×10−3
1.4 ×10−4
2.5×10−4
4.0×10−1
1.0×10−2
7.0 ×10−5
2.5×10−4
4.0×10−1
5.0×10−3
(a) rate = k[I2(aq)]n
[CH3COCH3(aq)]m
[H+
(aq)]p
p3-m1-n4-
p-2m-1n-4
5
-4
)10(5.0)10(4.0)10(2.5
)10(1.0)10(4.0)10(2.5
107.0
101.4
×××
×××
=
×
×
−
From experiments 3 and 4,
2 = 2p ⇒ p = 1
= 2p
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

32. 32
Initial rate
(mol L−1
s−1
)
Initial concentration
(mol L−1
)
[I2
(aq)] [CH3
COCH3
(aq)] [H+
(aq)]
3.5 ×10−5
2.5×10−4
2.0×10−1
5.0×10−3
3.5 ×10−5
1.5×10−4
2.0×10−1
5.0×10−3
1.4 ×10−4
2.5×10−4
4.0×10−1
1.0×10−2
7.0 ×10−5
2.5×10−4
4.0×10−1
5.0×10−3
(a) Rate = k[I2(aq)]0
[CH3COCH3(aq)][H+
(aq)]
= k[CH3COCH3(aq)][H+
(aq)]
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

33. 33
Initial rate
(mol L−1
s−1
)
Initial concentration
(mol L−1
)
[I2
(aq)] [CH3
COCH3
(aq)] [H+
(aq)]
3.5 ×10−5
2.5×10−4
2.0×10−1
5.0×10−3
3.5 ×10−5
1.5×10−4
2.0×10−1
5.0×10−3
1.4 ×10−4
2.5×10−4
4.0×10−1
1.0×10−2
7.0 ×10−5
2.5×10−4
4.0×10−1
5.0×10−3
(b) Rate = k[CH3COCH3(aq)][H+
(aq)]
From experiment 1,
3.5×10−5
= k(2.0×10−1
)(5.0×10−3
)
k = 0.035 mol−1
L1
s−1
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

34. 34
Determination ofDetermination of
Rate LawRate Law
byby
Graphical MethodsGraphical Methods
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

35. 35
The rate of a reaction may be expressed
as : -
(1) Differential rate equation
(2) Integrated rate equation
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

36. 36
A → products
n
k[A]
dt
d[A]
Rate =−=
(Differential rate equation)
shows the variation of rate with [A]
Two types of plots to determine k and n
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

37. 37
[A]
rate
n
k[A]
dt
d[A]
rate =−=
n = 0k
rate = k
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR
Concentration of reactant A

38. 38
Examples of zero-order reactions : -
2NH3(g) N2(g) + 3H2(g)
Fe or W as catalyst
Decomposition of NH3/HI can take place only
on the surface of the catalyst.
Once the surface is covered completely
(saturated) with NH3/HI molecules at a given
concentration of NH3/HI, further increase in
[NH3]/[HI] has no effect on the rate of
reaction.
2HI(g) H2(g) + I2(g)
Au as catalyst
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

39. 39
[A]
rate
nk
dt
d[A]
rate [A]=−=
n = 1
slope = k
linear
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR
Concentration of reactant A

40. 40
[A]
rate
2
k[A]
dt
d[A]
rate =−=
n = 2
k cannot be determined directly
from the graph
parabola
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR
Concentration of reactant A

41. 41
n
k[A]
dt
d[A]
rate =−=
[A]
rate n = 2
n = 1
n = 0
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR
Concentration of reactant A

42. 42 log10[A]
log10rate
n
k[A]rate =
n
1010 k[A]logratelog =
slope
y-intercept
n = 0
n = 1
log10k
n = 2
[A]nlogklog 1010 +=
slope = 1
slope = 2
slope = 0
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

43. 43
n
k[A]
dt
d[A]
=− (Differential rate equation)
kdtd[A] −=
∫ ∫−=
t
0 0
A
A
t
t
dtkd[A]
kt[A][A] 0t −=−
[A]t = [A]0 – kt (Integrated rate
equation)
If n = 0
Derivation not required
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

44. 44
[A]t = [A]0 – kt (Integrated rate equation)
shows variation of [A] with time
time
[A]t
ratek
dt
d[A]
slope −=−==
[A]0
constant rate
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR
ConcentrationofreactantA
t
AA
k t][][ 0 −
=

45. 45
n
k[A]
dt
d[A]
=− (Differential rate equation)
(Integrated rate
equation)
If n = 1, k[A]
dt
d[A]
=−
kdt
[A]
d[A]
−=
∫ ∫−=
t
0 0
[A]
[A]
t
t
dtkd[A]
[A]
1
loge[A]t – loge[A]0 = −kt
Or [A]t = [A]0 e−kt
loge[A]t = loge[A]0 − kt
ln
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

46. 46
Two types of plots to determine k and n
Or [A]t = [A]0 e−kt
loge[A]t = loge[A]0 − kt
time
log[A]t
log[A]0
slope = −k/2.303 k= -2.303xslpoe
linear → n = 1
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR
][
][
log
303.2 0
tA
A
t
k =
intercept = log[A]0
[A]0=antilog (intercept)

47. 47
Two types of plots to determine k and n
Or [A]t = [A]0 e−kt
loge[A]t = loge[A]0 − kt
time
[A]t
[A]t varies exponentially with time
constant half life → n = 1
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

48. 48
seconds100tlife,half
2
1 =
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

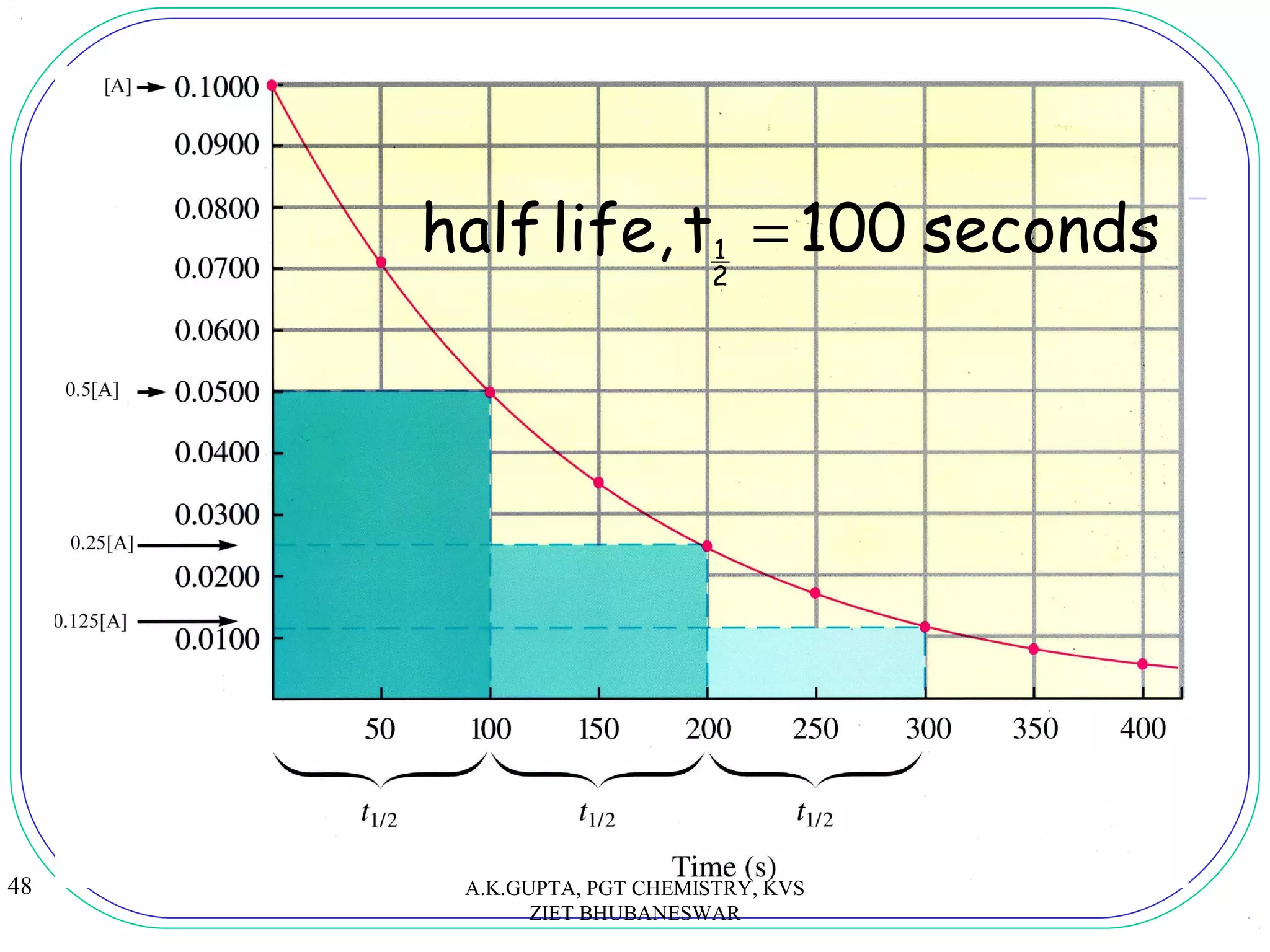
49. 49
2
1ttwhen = 0t [A]
2
1
[A] =
693.0301.0303.2
k
log2
303.2t
2
1 === x
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR
tA
A
t
k
][
][
log
303.2 0
=

50. 50
seconds100tlife,half
2
1 =
s100
2.303log2
k = = 6.9×10−3
s−1
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

51. 51
Question
For hydrolysis
sucrose → fructose + glucose
Rate = k[sucrose] k = 0.208 h−1
at 298 K
a. Determine the rate constant of the
reaction.
b. Calculate the time in which 87.5%of
sucrose has decomposed
(a) h3.33
h0.208
12.303x0.30
k
2.303log2
t 12
1 === −
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

52. 52
Q.17
sucrose → fructose + glucose
Rate = k[sucrose] k = 0.208 h−1
at 298 K
(b)
87.5% decomposed → [A]t = 0.125[A]0
On solving we get = 9.99 h
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR
tA
A
t
k
][
][
log
303.2 0
=
0
0
][125.0
][
log
303.2
A
A
k
t =

53. 53
mol−1
L1
s−1
kagainst t2
s−1−k/2.303log[A]t
against t1
mol L−1
s−1−k[A]t
against t[A]t
= [A]0
– kt0
Units of kSlope
Straight line
plot
Integrated
rate
equation
Order
t[A]
1
kt
[A]
1
[A]
1
0t
+=
kt/2.303
[A]
[A]
log
0
t
−=
Summary : - For reactions of the type
A → Products
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

54. 54
2H2O2(aq) → 2H2O(l) + O2(g)
Rate = k[H2O2(aq)]
Examples of First Order ReactionsExamples of First Order Reactions
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

55. 55
Examples of First Order ReactionsExamples of First Order Reactions
Reaction Rate equation
2N2O5(g) → 4NO2(g) + O2(g) Rate = k[N2O5(g)]
SO2Cl2(l) → SO2(g) + Cl2(g) Rate = k[SO2Cl2(l)]
(CH3)3CCl(l) + OH-
(aq)
→ (CH3)3COH(l) + Cl-
(aq)
Rate = k[(CH3)3CCl(l)]
(SN1)
All radioactive decays e.g. Rate = k[Ra]
SN1 : 1st
order Nucleophilic Substitution Reaction
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

56. 56
1. For a reaction involving one reactant only:
2NOCl(g) → 2NO(g) + Cl2(g)
Rate = k[NOCl(g)]2
2NO2(g) → 2NO(g) + O2(g)
Rate = k[NO2(g)]2
Examples of Second Order ReactionsExamples of Second Order Reactions
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

57. 57
Examples of Second Order ReactionsExamples of Second Order Reactions
Reaction Rate equation
H2(g) + I2(g) → 2HI(g) Rate = k[H2(g)][I2(g)]
CH3Br(l) + OH−
(aq)
→ CH3OH(l) + Br−
(aq)
Rate = k[CH3Br(l)][OH−
(aq)] (SN2)
CH3COOC2H5(l) + OH−
(aq)
→ CH3COO−
(aq) + C2H5OH(l)
Rate = k[CH3COOC2H5(l)][OH−
(aq)]
SN2 : 2nd
order Nucleophilic Substitution Reaction
2. For a reaction involving one reactant only:
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

58. 58
2. For a reaction involving two reactants:
A + B → products
Rate = k[A][B]
To determine the rate equation, the concentration
of one of the reactants must be kept constant
(in large excess) such that the order of reaction
w.r.t. the other reactant can be determined.
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

59. 59
2. For a reaction involving two reactants:
A + B → products
Rate = k[A][B]
When [B] is kept constant,
excess
rate = k’[A] (where k’ = k[B]excess)
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

60. 60
Rate = k[A][B]excess = k’[A]
k can be determined from k’ if [B]excess is known
Linear → first order
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

61. 61
2. For a reaction involving two reactants:
A + B → products
Rate = k[B][A]
• When [A] is kept constant,
rate = k”[B] (where k” = k[A]excess)
excess
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

62. 62
Rate = k[A]excess[B] = k’’[B]
k can be determined from k’’ if [A]excess is known
Linear → first order
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

63. 63
Rate Equations and Order of Reactions
(a) The reaction between tyrosine (an amino acid) and
iodine obeys the rate law: rate = k [Tyr] [I2].
Write the orders of the reaction with respect to tyrosine
and iodine respectively, and hence the overall order.
Answer(a) The order of the reaction with respect to
tyrosine is 1, and the order of the reaction
with respect to iodine is also 1. Therefore, the
overall order of the reaction is 2.
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

64. 64
Rate Equations and Order of Reactions
(b) Determine the unit of the rate constant (k) of the
following rate equation:
Rate = k [A] [B]3
[C]2
(Assume that all concentrations are measured in
mol dm–3
and time is measured in minutes.)
Answer
(b)  k =
∴ Unit of k =
= mol-5
dm15
min-1
23
]C[]B][A[
Rate
63-
-1-3
)dm(mol
mindmmol
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

65. 65
The initial rate of a second order reaction is 8.0 × 10–3
mol
dm–3
s–1
. The initial concentrations of the two reactants,
A and B, are 0.20 mol dm–3
. Calculate the rate constant of
the reaction and state its unit.
Zeroth, First and Second Order Reactions
Answer
8.0 × 10-3
= k × (0.20)2
∴ k = 0.2 mol-1
dm3
s-1
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

66. 66
Determination of Simple Rate Equations from Initial Rate
Method
For a reaction between two substances A and B,
experiments with different initial concentrations of A and
B were carried out. The results were shown as follows:
Expt Initial conc. of A
(mol L-1
)
Initial conc. of
B (mol L-1
)
Initial rate
(mol L-1
s-1
)
1 0.01 0.02 0.0005
2 0.02 0.02 0.001 0
3 0.01 0.04 0.002 0
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

67. 67
Determination of Simple Rate Equations from Initial Rate Method
(a) Calculate the order of reaction with respect to A
and that with respect to B.
Answer
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

68. 68
Determination of Simple Rate Equations from Initial Rate Method
(a) Let x be the order of reaction with respect to A, and y be the
order of reaction with respect to B. Then, the rate equation for
the reaction can be expressed as:
Rate = k [A]x
[B]y
Therefore,
0.0005 = k (0.01)x
(0.02)y
.......................... (1)
0.0010 = k (0.02)x
(0.02)y
.......................... (2)
0.002 0 = k (0.01)x
(0.04)y
.......................... (3)
Dividing (1) by (2),
∴ x = 1
x
)
02.0
01.0
(
0010.0
50.000
=
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

69. 69
Determination of Simple Rate Equations from Initial Rate Method
(a) Dividing (1) by (3),
∴ y = 2
y
)
04.0
02.0
(
0010.0
50.000
=
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

70. 70
Determination of Simple Rate Equations from Initial Rate Method
(b) Using the result of experiment (1),
Rate = k [A] [B]2
0.000 5 = k × 0.01 × 0.022
k = 125 mol-2
dm6
s-1
(c) Rate = 125 [A] [B]2
(b) Calculate the rate constant using the result of
experiment 1.
(c) Write the rate equation for the reaction.
Answer
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

71. 71
In the kinetic study of the reaction,
CO(g) + NO2(g) → CO2(g) + NO(g)
four experiments were carried out to determine the
initial reaction rates using different initial
concentrations of reactants. The results were as follows:
Determination of Simple Rate Equations from Initial Rate Method
Expt Initial conc.
of CO(g)
(mol dm-3
)
Initial conc.
of NO2(g)
(mol dm-3
)
Initial rate
(mol dm-3
s-1
)
1 0.1 0.1 0.015
2 0.2 0.1 0.030
3 0.1 0.2 0.030
4 0.4 0.1 0.060A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

72. 72
(a) Calculate the rate constant of the reaction, and hence
write the rate equation for the reaction.
14.3 Determination of Simple Rate Equations from Initial Rate Method
(SB p.31)
Answer
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

73. 73
14.3 Determination of Simple Rate Equations from Initial Rate Method
(SB p.31)
(a) Let m be the order of reaction with respect to CO, and n be the
order of reaction with respect to NO2. Then, the rate equation for
the reaction can be expressed as:
Rate = k [CO]m
[NO2]n
Therefore,
0.015 = k (0.1)m
(0.1)n
.......................... (1)
0.030 = k (0.2)m
(0.1)n
.......................... (2)
0.030 = k (0.1)m
(0.2)n
.......................... (3)
Dividing (1) by (2),
∴ m = 1
m
)
2.0
1.0
(
030.0
0.015
=
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

74. 74
Determination of Simple Rate Equations from Initial Rate Method
(a) Dividing (1) by (3),
∴ n = 1
∴ Rate = k [CO] [NO2]
Using the result of experiment (1),
0.015 = k (0.1)2
k = 1.5 mol-1
dm3
s-1
∴ Rate = 1.5 [CO] [NO2]
n
)
2.0
1.0
(
030.0
0.015
=
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

75. 75
Determination of Simple Rate Equations from Initial Rate Method
(b) Determine the initial rate of the reaction when the initial
concentrations of both CO( g) and NO2( g) are 0.3 mol
dm–3
.
Answer
(b) Initial rate = 1.5 × 0.3 × 0.3
= 0.135 mol dm-3
s-1
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

76. 76
(a) Write a chemical equation for the decomposition
of hydrogen peroxide solution.
Determination of Simple Rate Equations from Differential Rate Equations
Answer
(a) 2H2O2(aq) → 2H2O(l) + O2(g)
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

77. 77
(b) Explain how you could find the rate of
decomposition of hydrogen peroxide solution in
the presence of a solid catalyst using suitable
apparatus.
Determination of Simple Rate Equations from Differential Rate Equations
Answer
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

78. 78
Determination of Simple Rate Equations from Differential Rate Equations
(b) In the presence of a suitable catalyst such as manganese(IV)
oxide, hydrogen peroxide decomposes readily to give oxygen
gas which is hardly soluble in water. A gas syringe can be used
to collect the gas evolved. To minimize any gas leakage, all
apparatus should be sealed properly. A stopwatch is used to
measure the time. The volume of gas evolved per unit time (i.e.
the rate of evolution of the gas) can then be determined.
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

79. 79
(c) The table below shows the initial rates of
decomposition of hydrogen peroxide solution of
different concentrations. Plot a graph of the initial
rate against [H2O2(aq)].
Determination of Simple Rate Equations from Differential Rate Equations
Answer
[H2O2(aq)]
(mol L-1
)
0.100 0.175 0.250 0.300
Initial rate
(10-4
mol L-1
s-1
)
0.59 1.04 1.50 1.80
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

80. 80
14.4 Determination of Simple Rate Equations from Differential Rate Equations
(SB p.34)
(c)
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

81. 81
(d) From the graph in (c), determine the order and
rate constant of the reaction.
Determination of Simple Rate Equations from Differential Rate Equations
Answer
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

82. 82
Determination of Simple Rate Equations from Differential Rate Equations
(d) There are two methods to determine the order and rate constant
of the reaction.
Method 1:
When the concentration of hydrogen peroxide solution
increases from 0.1 mol dm–3
to 0.2 mol dm–3
, the reaction rate
increases from 0.59 × 10–4
mol dm–3
s–1
to about 1.20 × 10–4
mol dm–3
s–1
.
∴ Rate ∝ [H2O2(aq)]
Therefore, the reaction is of first order.
The rate constant (k) is equal to the slope of the graph.
k =
= 6.0 × 10-4
s-1
3-
-1-3
dmmol0)-.3000(
sdmmol0)-4-10(1.8×
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

83. 83
Determination of Simple Rate Equations from Differential Rate Equations
(d) Method 2:
The rate equation can be expressed as:
Rate = k [H2O2(aq)]x
where k is the rate constant and x is the order of reaction.
Taking logarithms on both sides of the rate equation,
log (rate) = log k + x log [H2O2(aq)] ................. (1)
-3.74-3.82-3.98-4.23log (rate)
-0.523-0.602-0.757-1.000log
[H2O2(aq)]
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

84. 84
Determination of Simple Rate Equations from Differential Rate Equations
(d) A graph of log (rate) against log [H2O2(aq)] gives a straight line
of slope x and y-intercept log k.
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

85. 85
Determination of Simple Rate Equations from Differential Rate Equations
(d) Slope of the graph =
=1.0
∴ The reaction is of first order.
Substitute the slope and one set of value into equation (1):
-4.23 = log k + (1.0) (-1.000)
log k = -3.23
k = 5.89 × 10-4
s-1
)8.0(5.0
)02.4(71.3
−−−
−−−
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

86. 86
Determination of Simple Rate Equations from Differential Rate Equations
(a) Decide which curve in the following graph corresponds
to
(i) a zeroth order reaction;
(ii) a first order reaction.
(a) (i) (3)
(ii) (2)
Answer
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

87. 87
Determination of Simple Rate Equations from Differential Rate Equations
(b) The following results were obtained for the
decomposition of nitrogen(V) oxide.
2N2O5(g) → 4NO2(g) + O2(g)
Concentration of N2O5
(mol dm-3
)
Initial rate (mol dm-3
s-1
)
1.6 × 10-3 0.12
2.4 × 10-3 0.18
3.2 × 10-3 0.24
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

88. 88
Determination of Simple Rate Equations from Differential Rate Equations
(i) Write the rate equation for the reaction.
Answer
(i) The rate equation for the reaction can be
expressed as:
Rate = k [N2O5(g)]m
where k is the rate constant and m is the
order of reaction.
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

89. 89
Determination of Simple Rate Equations from Differential Rate Equations
(ii) Determine the order of the reaction.
Answer
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

90. 90
Determination of Simple Rate Equations from Differential Rate Equations
(ii) Method 1:
A graph of the initial rates against [N2O5(g)] is shown as follows:
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

91. 91
Determination of Simple Rate Equations from Differential Rate Equations
As shown in the graph, when the concentration of N2O5 increases
from 1.0 × 10–3
mol dm–3
to 2.0 × 10–3
mol dm–3
, the rate of the
reaction increases from 0.075 mol dm–3
s–1
to 0.15 mol dm–3
s–1
.
∴ Rate ∝ [N2O5(g)]
∴ The reaction is of first order.
Then, the rate constant k is equal to the slope of the graph.
k =
= 75 s-1
∴ The rate equation for the reaction is:
Rate = 75 [N2O5(g)]
1-3-3-
-1-3
sdmmol0)-10.61(
sdmmol0)(0.12
×
−
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

92. 92
Determination of Simple Rate Equations from Differential Rate Equations
(iii) Determine the initial rate of reaction when the
concentration of nitrogen(V) oxide is:
(1) 2.0 × 10–3
mol dm–3
.
(2) 2.4 × 10–2
mol dm–3
.
Answer
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

93. 93
Determination of Simple Rate Equations from Differential Rate Equations
(iii) The rate equation, rate = 75 [N2O5(g)], is used for the
following calculation.
(1) Rate = 75 [N2O5(g)]
= 75 s–1
× 2.0 × 10–3
mol dm–3
= 0.15 mol dm–3
s–1
(2) Rate = 75 [N2O5(g)]
= 75 s–1
× 2.4 × 10–2
mol dm–3
= 1.8 mol dm–3
s–1
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

94. 94
The half-life of a radioactive isotope A is 1 997
years. How long does it take for the radioactivity of
a sample of A to drop to 20% of its original level?
Determination of Simple Rate Equations from Integrated Rate Equations
Answer
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

95. 95
Determination of Simple Rate Equations from Integrated Rate Equations
As radioactive decay is a first order reaction,
= 3.47 × 10-4
year-1

∴ t = 4638 years
∴ It takes 4638 years for the radioactivity of a sample of A to
dropt to 20 % of its original level.
k
t
693.0
2
1 =
1997
693.0
=k
kt=)
[A]
[A]
(ln 0
t4
10473.)
%20
%100
(ln −
×=
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

96. 96
Determination of Simple Rate Equations from Integrated Rate Equations
(a) At 298 K, the rate constant for the first order
decomposition of nitrogen(V) oxide is 0.47 × 10–4
s–1
.
Determine the half-life of nitrogen(V) oxide at 298 K.
N2O5 → 2NO2 + O2
2
1
Answer
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

97. 97
Determination of Simple Rate Equations from Integrated Rate Equations
(a) Let the half-life of nitrogen(V) oxide be .
∴ The half-life of nitrogen(V) oxide is 14 745 s.
2
1
t
2
1
14 693.0
s1047.0
t
=× −−
s74514
2
1 =t
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

98. 98
(b) The decomposition of CH3N = NCH3 to form N2 and
C2H6 follows first order kinetics and has a half-life of
0.017 minute at 573 K. Determine the amount of
CH3N = NCH3 left if 1.5 g of CH3N = NCH3 was
decomposed for 0.068 minute at 573 K.
Determination of Simple Rate Equations from Integrated Rate Equations
Answer
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR

99. 99
Determination of Simple Rate Equations from Integrated Rate Equations
(b)
Let m be the amount of CH3N=NCH3 left after 0.068
minute.
m = 0.094 g
1
2
1
min76.40
min017.0
693.0693.0 −
===
t
k
0.06840.76)
1.5
(ln ×=
m
A.K.GUPTA, PGT CHEMISTRY, KVS
ZIET BHUBANESWAR