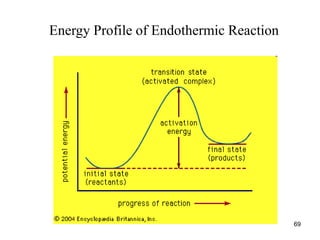
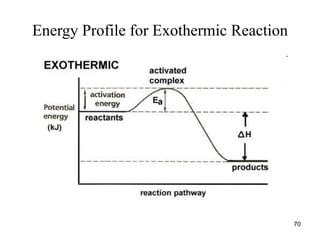
The document covers key concepts in chemical kinetics, including the expression of reaction rates, determination of reaction orders, and the methods used to derive rate laws. It outlines various types of rates (initial, instantaneous, and average) and emphasizes the importance of rate laws in understanding reaction mechanisms at a molecular level. Additionally, it details the graphical methods for determining rate laws and explores the half-lives of reactions and the relationship between concentration and reaction rates.

1. Chemical Kinetics
• Expression of rates.
• Stoichiometric relationships of rates of different
substances in a reaction.
• Determination of reaction orders, rate laws, and rate
constant by method of initial rate.
• Determination of rate laws by graphical or integration
method.
• Determination of half-lives
• Determination of activation energy
• Elementary steps and reaction mechanism
• Effect of catalysts
1

2. Chemical Kinetics
• The study of reaction rates;
– How fast does a reaction proceeds and what
factors affecting it;
– A measure of the change of the concentration of a
reactant (or a product) as a function of time.
• The study of rate yields information on the
mechanism by which a reaction occurs at
molecular level.
2

3. Types of Rates
• Initial Rates
– Rates measured at the beginning of the reaction,
which is dependent on the initial concentrations of
reactants.
• Instantaneous Rates
– Rates measured at any point during the reaction.
• Average Rates
– An overall rate measured over a period or time
interval.
3

4. Rate of reaction between phenolphthalein with
excess base.
• Experimental Data for the Reaction Between Phenolphthalein and Base
• Concentration of
Phenolphthalein (M) Time (s)
– 0.0050 0.0
– 0.0045 10.5
– 0.0040 22.3
– 0.0035 35.7
– 0.0030 51.1
– 0.0025 69.3
– 0.0020 91.6
– 0.0015 120.4
– 0.0010 160.9
– 0.00050 230.3
– 0.00025 299.6
– 0.00015 350.7
– 0.00010 391.2
4

5. Instantaneous Rate:
Rate of decrease in [Phenolphthalein]
5

6. Instantaneous Rate
• Value of the rate at a particular time.
• Can be obtained by computing the slope
of a line tangent to the curve at that
point.
6

7. The Decomposition of Nitrogen Dioxide
7

8. The Decomposition of Nitrogen Dioxide
8

9. Average Rate
• Consider the following reaction at 300o
C:
2 NO2(g)  2 NO(g) + O2(g)
• The initial concentration of NO2 is 0.0100 mol/L and
its concentration after 150 s is 0.0055 mol/L. What
are the average rates of this reaction during the first
150 s and during the second 150 s?
9

10. Average rate during the first 150 s
• Solution:
• Average rate =
• =
• =
• = 3.0 x 10-5
mol/(L.s)
t
]
[NO
- 2


s
150
mol/L)
0.0100
-
mol/L
(0.0055
-
s
150
mol/L
0.0045
10

11. Average rate during the second 150 s
• Solution:
• Average rate =
• =
• =
• = 1.1 x 10-5
mol/(L.s)
• Average rate decreases as reaction progresses
because the reactant concentration has decreased
t
]
[NO
- 2


s
150
mol/L)
0.0055
-
mol/L
(0.0038
-
s
150
mol/L
0.0017
11

12. Rate Law
• Shows how the rate depends on the
concentrations of reactants.
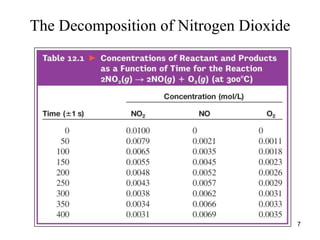
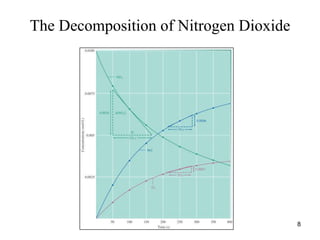
• For the decomposition of nitrogen dioxide:
2NO2(g) → 2NO(g) + O2(g)
Rate = k[NO2]n:
 k = rate constant
 n = order of the reactant
12

13. Rate Law
Rate = k[NO2]n
• The concentrations of the products do not
appear in the rate law because the reaction
rate is being studied under conditions where
the reverse reaction does not contribute to the
overall rate.
13

14. Rate Law
Rate = k[NO2]n
• The value of the exponent n must be
determined by experiment; it cannot be
written from the balanced equation.
14

15. Rate Law
• An expression or equation that relates the rate
of reaction to the concentrations of reactants at
constant temperature.
• For the reaction:
R1 + R2 + R3  Products
Rate = k[R1]x
[R2]y
[R3]z
Where k = rate constant; x, y, and z are the rate orders
with respect to individual reactants. Rate orders are
determined experimentally.
15

16. Types of Rate Laws
• Differential Rate Law (rate law) – shows
how the rate of a reaction depends on
concentrations.
• Integrated Rate Law – shows how the
concentrations of species in the reaction
depend on time.
16

17. Rate Laws: A Summary
• Our rate laws involve only concentrations of
reactants, because we typically consider
reactions only under conditions where the
reverse reaction is unimportant,
17

18. Rate Laws: A Summary
• Experimental convenience usually dictates
which type of rate law is determined
experimentally.
• Knowing the rate law for a reaction is
important mainly because we can usually infer
the individual steps involved in the reaction
from the specific form of the rate law.
18

19. Rate Order
• The power or exponent of the concentration of
a given reactant in the rate law. It indicates the
degree in which the rate depends on the
concentration of that particular reactant.
• The sum of the powers of the concentrations is
referred to as the overall order for the reaction.
19

20. Expressions of Reaction Rates and Their
Stoichiometric Relationships
• Consider the reaction:
2N2O5  4NO2 + O2
• Rate of disappearance of N2O5 =
• Rate of formation of NO2 =
• Rate of formation of O2 =
• Stoichiometric relationships of these rates
•
t
]
NO
[ 2


t
]
[O2


t
]
O
[N 5
2



t
]
[O
)
t
]
NO
[
(
4
1
)
t
]
O
[N
(
2
1 2
2
5
2









20

21. Expressions of Reaction Rates
• For a general reaction,
aA + bB  cC + dD,
• the reaction rate can be written in a number of
different but equivalent ways,
21

22. Rate Laws
• For a general reaction,
aA + bB + eE  Products
• The rate law for this reaction takes the form:
• where k is called the "rate constant."
• x, y, and z, are small whole numbers or simple
fractions and they are the rate order with respect to
[A], [B], and [E]. The sum of x + y + z + . . . is called
the “overall order" of the reaction.
22

23. Types of Rate Laws
• Consider a general reaction:
aA + bB  Products
• The rate law is expressed as,
Rate = k[A]x
[B]y
,
Where the exponents x and y are called the rate
order of the reaction w.r.t. the respective reactants;
These exponents are usually small integers or simple
fractions.
23

24. Types of Rate Laws
1. Zero-Order Reactions
1. In a zero order reaction the rate does not depend
on the concentration of reactant,
2. For example, the decomposition of HI(g) on a
gold catalyst is a zero-order reaction;
3. 2 HI(g)  H2(g) + I2(g)
4. Rate = k[HI]0
= k;
(The rate is independent on the concentration of HI)
24

25. Types of Rate Laws
• First Order Reactions
In a first order reaction the rate is proportional to
the concentration of one of the reactants.
Example, for first-order reaction:
2N2O5(g)  4NO2(g) + O2(g)
• Rate = k[N2O5],
The rate of decomposition of N2O5 is proportional
to [N2O5], the molar concentration of N2O5
25

26. Types of Rate Laws
• Second Order Reactions
In a second order reaction, the rate is proportional
to the second power of the concentration of one of
the reactants.
Example, for the decomposition of NO2 follows
second order w.r.t. [NO2]
2NO2(g)  2NO(g) + O2(g)
• Rate = k[NO2]2
26

27. Determination of Rate Law using Initial Rate
• Consider the following reaction:
S2O8
2-
(aq) + 3I-
(aq)  2SO4
2-
(aq) + I3
-
(aq)
27

28. Determination of Rate Law using Initial Rate
Reaction: S2O8
2-
(aq) + 3I-
(aq)  2SO4
2-
(aq) + I3
-
(aq)
• The following data were obtain.
• 
• Expt. [S2O8
2-
] [I-
] Initial Rate,
• # (mol/L) (mol/L) (mol/L.s)
• 
• 1 0.036 0.060 1.5 x 10-5
• 2 0.072 0.060 2.9 x 10-5
• 3 0.036 0.120 2.9 x 10-5
• 
28

29. Determination of Rate Law using Initial Rate
Reaction: S2O8
2-
(aq) + 3I-
(aq)  2SO4
2-
(aq) + I3
-
(aq)
• (a) Determine the order of the reaction w.r.t. each
reactant. Write the rate law for the above reaction.
• (b) Calculate the rate constant, k, and give its
appropriate units.
• (c) Calculate the reaction rate when each reactant
concentration is 0.20 M
29

30. Determination of Rate Law using Initial Rate
• Solution: The rate law = Rate = k[S2O8
2-
]x
[I-
]y
,
here x and y are rate orders.
• (a) Calculation of rate order, x:
•
1
2
2
~
mol/L.s
10
x
1.5
mol/L.s
10
x
2.9
2
)
060
.
0
(
)
036
.
0
(
)
060
.
0
(
)
072
.
0
(
]
[I
]
O
[S
]
I
[
]
O
[S
5
-
5
-
1
-
1
-
2
8
2
3
-
2
-
2
8
2






y
M
M
k
M
M
k
k
k
x
x
y
x
y
x
y
x
y
x
30

31. Determination of Rate Law using Initial Rate
• (b) Calculation of rate order, y:
•
• This reaction is first order w.r.t. [S2O8
2-
] and [I-
]
• Rate = k[S2O8
2-
][I-
]
1
2
2
~
mol/L.s
10
x
1.5
mol/L.s
10
x
2.9
2
)
060
.
0
(
)
036
.
0
(
)
120
.
0
(
)
036
.
0
(
]
[I
]
O
[S
]
I
[
]
O
[S
5
-
5
-
1
-
-
2
8
2
3
-
-
2
8
2






y
M
M
k
M
M
k
k
k
y
y
y
x
y
x
y
x
y
x
31

32. Calculating rate constant and rate at different
concentrations of reactants
• Rate constant, k =
• = 6.6 x 10-3
L.mol-1
.s-1
• If [S2O8
2-
] = 0.20 M, [I-
] = 0.20 M, and
– k = 6.6 x 10-3
L.mol-1
.s-1
• Rate = (6.6 x 10-3
L.mol-1
.s-1
)(0.20 mol/L)2
• = 2.6 x 10-4
mol/(L.s)
mol/L)
60
mol/L)(0.0
(0.038
mol/L
10
x
1.5 -5
32

33. Integrated Rate Law
• Graphical method to derive the rate law
of a reaction:
• Consider a reaction with single reactant:
• R  Products
• If the reaction is zero-order w.r.t. [R],
• Then,
k
Rate
t
[R]
-




33

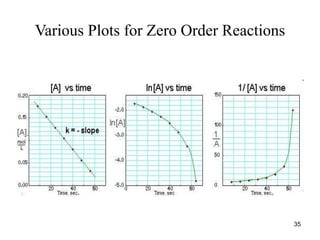
34. Graphical Method for Zero-Order Reaction
k
Rate
t
[R]
-




[R] = -kt, and [R]t = [R]0 = kt;
A plot of [R]t versus t yields a straight
line with k = -slope.
34

35. Various Plots for Zero Order Reactions
35

36. Graph of Zero-order Reactions
• Plot of [R]t versus t:
[R]t
t
slope = -k
36

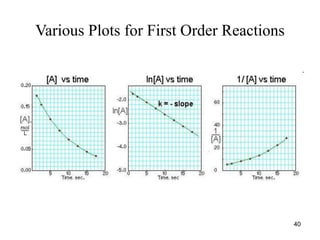
37. Graphical Method for First Order Reactions
• If the reaction: R  Products is a first order
reaction, then
• Which yields:
• And a plot of ln[R]t versus t will yield a straight line
with slope = -k and y-intercept = ln[R]0
[R]
t
[R]
-
k
Rate 



t
-
ln[R]
ln[R]
t;
-
[R]
[R]
0
t k
k 


37

38. Graph of First Order Reactions
Plot of ln]R]t versus t:
ln[R]t
t
slope = -k
38

39. Plots of [A] and ln[A] versus time for First Order
Reactions
39

40. Various Plots for First Order Reactions
40

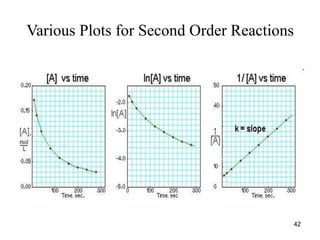
41. Graphical Method for Second Order Reactions
• If the reaction: R  Products follows second-
order kinetics, then
• or
•
• and
• A plot of 1/[R]t versus t will yield a straight line
with slope = k and y-intercept = 1/[R]0
2
[R]
t
[R]
-
k
Rate 


 t
[R]
[R]
2



k
[R]
1
t
[R]
1
0
t

 k
41

42. Various Plots for Second Order Reactions
42

43. Graph of Second-order Reactions
• Plot of 1/[R]t versus time:
t
R]
[
1
time
slope = k
43

44. Plots of concentration versus time for first
and second order reactions
44

45. Plots of ln[Concentration] versus time
45

46. Plots of 1/[Concn.] versus time
46

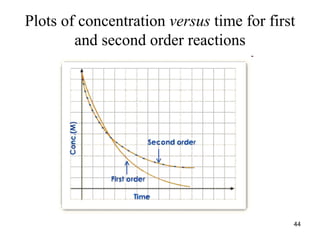
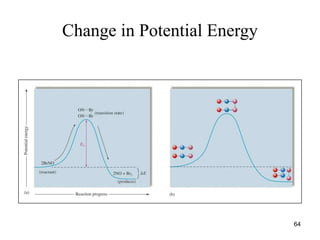
47. Characteristics of plots for zero, first, and second
order reactions
• The graph that is linear indicates the order of the
reaction with respect to A (reactant):
• For a zero order reaction, Rate = k (k = - slope)
• For a 1st order reaction, Rate = k[A] (k = - slope)
• For a 2nd order reaction, Rate = k[A]2
(k = slope)
• For zero-order reaction, half-life, t1/2 = [R]0/2k;
• For first order reaction, half-life, t1/2 = 0.693/k;
• For second order reaction, half-life, t1/2 = 1/k[R]0;
47

48. Half-Lives of Reactions
• For zero-order reaction: t1/2 = [R]0/2k;
• For first-order reaction: t1/2 = 0.693/k;
• For second-order reaction: t1/2 = 1/(k[R]0)
• Note: For first-order reaction, the half-life is
independent of the concentration of reactant, but for
zero-order and second-order reactions, the half-lives
are dependent on the initial concentrations of the
reactants.
48

49. Half-Life of Reactions
49

50. Rate Laws
50

51. Summary of the Rate Laws
51

52. Exercise
Consider the reaction aA  Products.
[A]0 = 5.0 M and k = 1.0 x 10–2 (assume the
units are appropriate for each case). Calculate
[A] after 30.0 seconds have passed, assuming
the reaction is:
a) Zero order
b) First order
c) Second order
4.7 M
3.7 M
2.0 M
52

53. Reaction Mechanism
• The detail pictures of how a given reaction occurs at
molecular level
• It consists of a set of elementary steps that shows
probable reactions involving molecular species –
including reaction intermediates.
• The sum of these elementary steps yields the overall
balanced equation for the reaction.
53

54. Elementary Steps
• For example, the overall reaction:
2A + B  C + D
• may involves the following elementary steps in
its mechanism:
• Step-1: A + B  X;
• Step-2: X + A  Y;
• Step-3: Y  C + D
• Overall reaction: 2A + B  C + D;
54

55. Molecularity in Elementary Steps
• Molecularity in the number of molecular species that react in
an elementary process.
• Rate Law for Elementary Processes:
• Elementary Reactions Molecularity Rate Law
• 
• A  product Unimolecular Rate = k[A]
• 2A  product Bimolecular Rate = k[A]2
• A + B  product Bimolecular Rate = k[A][B]
• 2A + B  product Termolecular Rate = k[A]2
[B]
• 
55

56. A Molecular Representation of the Elementary
Steps in the Reaction of NO2 and CO
NO2(g) + CO(g) → NO(g) + CO2(g)
56

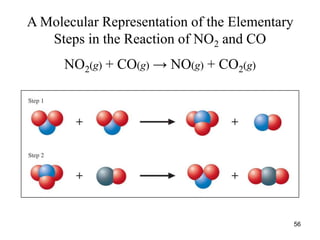
57. Reaction Mechanism
• Step-1: NO2 + NO2  NO3 + NO
• Step-2: NO3 + CO  NO2 + CO2
• Overall: NO2 + CO  NO + CO2
• The experimental rate law is Rate = k[NO2]2
• Which implies that the above reaction is second-order
w.r.t. NO2 , but is zero-order in [CO].
57

58. • The sum of the elementary steps
must give the overall balanced
equation for the reaction.
• The mechanism must agree with the
experimentally determined rate law.
Reaction Mechanism Requirements
58

59. Decomposition of N2O5
59

60. Decomposition of N2O5
2N2O5(g)  4NO2(g) + O2(g)
Step 1: N2O5 ⇌ NO2 + NO3 (fast)
Step 2: NO2 + NO3 → NO + O2 + NO2 (slow)
Step 3: NO3 + NO → 2NO2 (fast)
60

61. A Model for Chemical Reactions
For a reaction to occur:
1. Reactant molecules must collide;
2. Molecular collisions must occur with proper
orientations;
3. Collisions must be energetic and lead to the
formation of the transition-state complex;
4. The rate of formation of the transition-state
complex is the rate determining step;
5. The transition-state complex eventually leads to
the formation of products;
61

62. A Model for Reaction Kinetics
• All chemical reactions proceed through a transition-state
complex;
• An energy barrier called activation energy (Ea) must be
overcome to change reactants to the transition-state.
• The rate of formation of transition-state is the rate-
determining step for the overall reaction;
• The rate of formation of transition-state is dependent:
– on the frequency of effective molecular collisions, which
depends on the reactants concentrations;
– on the fraction of molecules with sufficient kinetic energy
to overcome the energy barrier, and
– on the reaction temperature
62

63. Transition States and Activation Energy
63

64. Change in Potential Energy
64

65. • Collision must involve enough energy to
produce the reaction (must equal or
exceed the activation energy).
• Relative orientation of the reactants must
allow formation of any new bonds
necessary to produce products.
For Reactants to Form Products
65

66. The Gas Phase Reaction of NO and Cl2
66

67. Dependence of Rate on Concentration
• This is contained in the rate law – that is, for
reaction:
aA + bB + cC  Products
Rate = k[A]x
[B]y
[C]z
;
67

68. Dependence of Rate on Temperature
• Rate depends on the fraction of “effective collisions”
per unit time.
– (Effective collisions are those with proper orientation and
sufficient energy to overcome activation energy Ea barrier.
• Thus rate depends on the activation energy and
temperature, such that,
– Higher activation energy implies high barrier and fewer
reactant molecules will form the transition-state complex.
This leads to a slower rate of reaction;
– Higher temperature results in a larger fraction of reactant
molecules with sufficient energy to overcome the energy
barrier. This leads to a faster rate of reaction.
68

69. Energy Profile of Endothermic Reaction
69

70. Energy Profile for Exothermic Reaction
70

71. Relationships between rate, rate constant,
activation energy, & temperature.
• Rate is dependent on rate constant, which is the
proportionality constant that relates rate to
concentrations (as depicted in the rate law).
• While rate constant is related to activation energy and
temperature by the Arrhenius equation:
• k = Ae-Ea/RT
• where A is Arrhenius collisional frequency factor, T is
the Kelvin temperature, and R is gas constant (R =
8.314 J/K.mol)
71

72. Graphical relationships of k, Ea, and T
• From Arrhenius equation: k = Ae-Ea/RT
ln(k) = ln(A) – (Ea/R)(1/T)
• The plot of ln(k) versus 1/T yields a straight line with the
slope = -(Ea/R), or Ea = -slope x R
• If k values are determined at two different temperatures,
such that at k1 at T1 and k2 at T2, then
ln(k2/k1) = (R = 8.314 J/K.mol)
)
T
1
-
T
1
)(
(
1
2
a
R
E

72

73. Exercise
Chemists commonly use a rule of thumb that
an increase of 10 K in temperature doubles
the rate of a reaction. What must the
activation energy be for this statement to be
true for a temperature increase from 25°C to
35°C?
Ea = 53 kJ
73

74. End of Slide
74