Chemical Kinetics

CHEMICAL KINETICS
Dr. Divya Sharma
Assistant Professor

Content
• Rate of reaction
• Factors which affect rate of reaction
• Rate law & Order of reaction
• Mechanism of reaction

CHEMICAL KINETICS
• Rate/speed of a chemical reaction ---- how chemical
process occurs.
• We study chemical kinetics, in point of industrial prospect---
-- determined rate of reaction by practically
• Besides information about the speed at which reactions
occur, kinetics also sheds light on the reaction mechanism
(exactly how the reaction occurs).Reactant Reactant Product

Rate of Reaction (ROR)
Rate = Speed -- Reaction speed (how fast does a chemical
reaction proceed)
• Change in concentration (in aqueous phase) or pressure (in
gaseous phase) of reactant/product with respect to time --
called Rate of Reaction
FACTORS AFFECT THE ROR:
• Temperature
• Reactant concentration
• Pressure of gaseous reactants or products

Rate of reaction (ROR)
For the reaction A --- B there are two ways of measuring
rate:
 The speed at which the reactants disappear
 The speed at which the products appear
i. Very Fast Reaction: Those chemical reaction which
completed within fraction of time. (like Ionic reactions)
NaCl + AgNO3 -- AgCl↓ + NaNO3
White ppt
Reaction proceed within microseconds. So, ROR cannot be
determined.
ii. Very Slow Reaction: Those chemical reaction which
completed in very long time duration.
Eg. Rusting of Iron

Rate of reaction (ROR)
iii. Moderate Reaction: Those chemical reaction which
completed in finite time.
Eg. All Molecular reactions
N2 + 3H2 ------ 2NH3
Reaction takes finite time to proceed. So, ROR can be
determined.ROR  Measure
Reactant disappear  Product appear

Rate of Reaction (ROR):
How to calculate Rate/ speed of any chemical reactions
by:
• Average rate of reaction
• Instantaneous rate of reaction

2A + 3B --------- 4C
If, Initial time => t = 0; Conc. a = a0 Conc. = 0
Final time => t = t; Conc. a = at (aFinal - aInitial) Conc. = X
Average ROR =
– ½ [∆A]/∆t = – ⅓ [∆B]/∆t = + ¼ [∆C]/∆t
Average ROR = Rate of change in concentration
Rate of change in time
Average Rate of Reaction
(ROR):

2X + Y --- 3Z
Average ROR =
– ½ [∆X]/∆t = – [∆Y]/∆t = + ⅓ [∆Z]/∆t
Rate of appearance (ROA): Product
ROA of Z = [∆Z]
∆ t
Rate of disappearance (ROD): Reactant
ROD of X = [∆X] ROD of Y = [∆Y]
∆ t ∆ t
(ROR):

Example: N2 + 3H2 ------ 2NH3
Average ROR =
– [∆N2]/∆t = – ⅓ [∆H2]/∆t = + ½ [∆NH3]/∆t
Rate of appearance (ROA): Product
ROA of NH3 = [∆NH3]
∆ t
Rate of disappearance (ROD): Reactant
ROD of N2 = [∆N2] ROD of H2 = [∆H2]
∆ t ∆ t
(ROR):

Unit of ROR = Rate of change in
concentration
Rate of change in
time
= Mol/Lit/sec => Mol L-1
s-1
In gaseous reaction
-1
Unit of ROR

Average ROR =
– ½ [∆N2O5]/∆t = + ¼ [∆NO2]/∆t = + [∆ O2]/∆t
Rate of appearance = [∆NO2] = 6Mol/L/s
∆ t
ROR = + ¼ [∆NO2]/∆t = + ¼ ˟ 6 = 1.5 Mol/L/sec
ROR = – ½ [∆N2O5]/∆t
1.5 = – ½ [∆N2O5]/∆t
3 Mol/L/sec = [∆ N2O5]
∆ t
Q. 2N2O5 ----------- 4NO2 + O2
If ROA of NO2 is 6Mol/L/sec. then,
find (i) ROR, and (ii) ROD of N2O5.

2A + 3B --- 4C
Initial time: ∆t = 0
Final time: ∆t = dt
Instantaneous ROR =
– ½ d[A]/ dt = – ⅓ d[B]/ dt = + ¼ d[C]/ dt
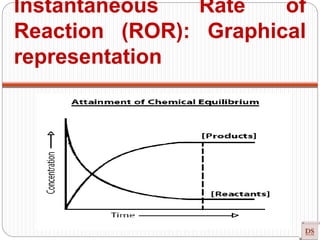
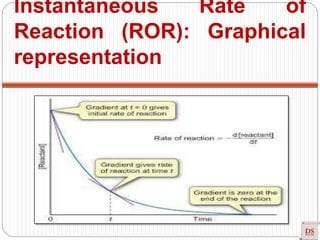
Instantaneous Rate of
Reaction (ROR):

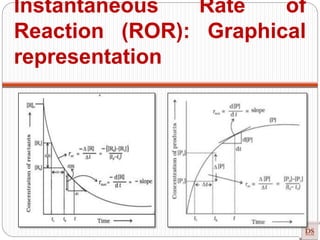
Instantaneous Rate of
Reaction (ROR): Graphical
representation

Slope = tan ɵ = d[A2 –
A1]/d(t2 – t1)
Slope = tan ɵ = d[B2 – B1]/
d(t2 – t1)
2A + 3B --- 4C
Instantaneous ROR =
–½d[A2 – A1]/d(t2 – t1) = – ⅓d[B2 – B1]/d(t2 – t1) = +¼d[C2 – C1]/d(t2 – t1)
Slope = tan ɵ = d[C2 – C1]/
d(t2 – t1)

Slope = tanɵ =
d[NH3]/dt
Slope = tanɵ =
d[O2]/dt
4NH3 + 5O2 -- 4NO + 6H2O
Instantaneous ROR =
–¼d[NH3]/dt = –⅕d[O2]/dt = +¼d[NO]/dt = +⅙d[H2O]/dt
Slope = tanɵ =
d[NO]/dt
Slope = tanɵ =
d[H2O]/dt

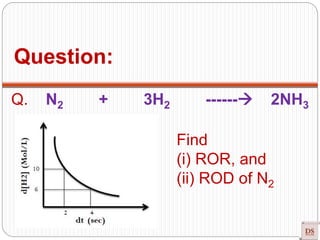
Q. N2 + 3H2 ------ 2NH3
Question:
Find
(i) ROR, and
(ii) ROD of N2

Q. N2 + 3H2 ------
2NH3
Find
(i) ROR, and
(ii) ROD of N2
Instantaneous ROR =
– d[N2]/ dt = – ⅓ d[H2]/ dt = + ½ d[NH3]/ dt
Slope = tan ɵ = (R2 – R1) = (6 - 10) = -2
(t2 – t1) (4 – 2)
ROR = – ⅓ d[H2]/dt
ROR = - ⅓ ˟ -2 => 2/3 Mol/L/sec
ROD = d[N2] = - d[N2] => 2/3 Mol/L/sec
dt dt

Factors of Rate of
Reaction (ROR)
Factors are affect the Rate of chemical reaction (how
fast does a reaction proceed)
FACTORS AFFECT THE ROR:
• Temperature
• Reactant concentration
• Pressure of gaseous reactants or products
• Action of catalyst
• Nature of reactant

i). Nature of Reactant
i. Very Fast Reaction: (like Ionic reactants)
NaCl + AgNO3 ---- AgCl↓ + NaNO3
Reaction proceed within microseconds. So, ROR cannot be
determined.
ROR ---- High
ii. Moderate Reaction: (Covalent reactants)
N2 + 3H2 ---- 2NH3
Reaction takes finite time to proceed. So, ROR can be
determined.

Homogenous reactants > Heterogenous reactants
Chemical nature α ROR
ROR α Stability of Product α 1
Stability of Reactant

ROR α Stability of Product α 1
Stability of Reactant
CH3COOH ----- CH3COO- + H+
HCOOH ----- HCOO- + H+
H-COO- > CH3-COO-
ROR more stable ROR less stable

Gas > Liquid > Solid
 Pressure of gaseous reactants or products  Due to increase number of
collision of molecules
ii). Physical state of
Reactant

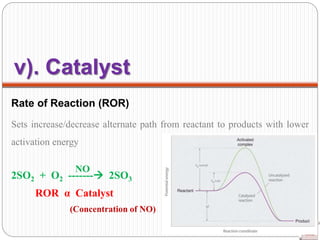
Rate of Reaction (ROR) ----- (mostly in
Solid state)
Surface area of a solid reactant  More area for
reactants to be in contact
ROR α Surface area of reactant
Eg: Sugar powder/solute (small molecules)
easily dissolve in milk/solvent/water than
sugar cubes. [Due to more surface area of
molecules].
iii). Surface area of
Reactant

Rate of Reaction (ROR) --(only in Photochemical/Photosensitive
reaction)
Chemical reactions, that occur on exposure to visible radiation are called
Photochemical reactions.
Some reactions are Photosensitive (light sensitive) ----
Photochemical reaction
H2 (g) + Cl2 (g) ------- 2HCl (g)
iv). Intensity of light
hʋ

 The rate of a photochemical reactions is affected by the intensity of light
 Temperature has little effect on photochemical reactions.
 Quantum yield or quantum efficiency of a photochemical reactions;
hʋ = number of reactant molecules in a given time / number of photon
(quanta) of light absorbed ill the same time
ROR α Intensity of light α Number of Photons
iv). Intensity of light

Sets increase/decrease alternate path from reactant to products with lower
activation energy
2SO2 + O2 ------- 2SO3
ROR α Catalyst
(Concentration of NO)
v). Catalyst
NO

 Generally, ROR increase on increasing temperature
 On 10ᵒ C rise in temperature, ROR increases 2-3 times (Temperature
coefficient).
ROR α Temperature
Arrhenius equation
vi). Temperature

 At higher temperature, reactant molecules have more kinetic energy,
move faster, and collide more often and with greater energy.
 Collision energy: when two chemicals react, their molecules have to
collide with each other (in a particular orientation) with sufficient energy
for the reaction to take place.
 Kinetic theory: Increasing temperature means the molecules move faster.
ROR α Temperature
vi). Temperature

 Generally, ROR increase on increasing concentration of reactants
(reactant molecules will collide)
 ROR may also decrease on increasing concentration of reactants
 ROR remains unaffected
 ROR may also depend upon products concentration
 ROR may depend on one or all or none of reactant concentration -- Rate
Law (depend on concentration of reactant)
ROR α Concentration of Reactant
vii). Concentration

Rate Law
Rate law explains the dependence of :
• Rate of reaction (ROR) on concentration of reactants or
products in reaction
• This dependence is very complex as it changes with
change in concentration of reactants or products
• We only study the simplest form of dependence
All steps are determined by only Experimental method

2A + B ------ 2C
Reactants Product
r = K [A]1 [B]2
Experimental method (ROR):
If, [A] ---- Double ROR ------- 2 times increase
ROR α [A]1
If, [B] ---- Double ROR ------- 4 times increase
ROR α [B]2
[⁖ ROR = r]
Rate Law of Expression
⁖ where as, K = Rate constant; [A] = Concentration of A reactant; [B] =
Concentration of B reactant; ROR = Rate of reaction; r = Rate law.

2A + B ------ 2C
Reactants Product
r = K [A]2 [B]1 This method followed
in only single step
reactions.
Guldberg & Wagge method:
If, [A] ---- Double ROR ------- 4 times increase
ROR α [A]2
If, [B] ---- Double ROR ------- 2 times increase
ROR α [B]1
[⁖ ROR = r]
Law of Mass Action
(as according stoichiometric coefficient)
⁖ where as, K = Rate constant; [A] = Concentration of A reactant; [B] = Concentration
of B reactant; ROR = Rate of reaction; r = Rate law.

2A + B ------ 2C
Reactants Product
r = K [A]x [B]y
Experimental method (ROR):
r α [A]x
r α [B]y
Rate Law of Expression
⁖ where as, K = Rate constant; [A] = Concentration of A reactant (Mol/Lit); [B] =
Concentration of B reactant (Mol/Lit); r = Rate law/ Rate of reaction; x = Order of
reaction with respect to A; y = Order of reaction with respect to B.

2A + B ------ 2C
Reactants Product
n = x + y
Order of Reaction (denoted as “n”)
n = overall order of reaction/ Total order of reaction/ order of reaction
Order of Reaction
(Can be negative or positive or zero or fractional)
⁖ where as, n = Order of reaction; x = Order of reaction with respect to A; y =
Order of reaction with respect to B.

2A + B ------ 2C
Reactants Product
Rate Law --- by experimental method (ROR):
K = Rate constant/ velocity constant/ specific reaction rate (per unit)
r α [A]x [B]y
If, concentration of all reactants or products in rate law expression is unity (1)
[A] = [B] = 1
K = Specific reaction rate (per unit)
r = K [A]x [B]y
r = K

Unit of Rate Constant (K)
Unit of ROR = Mol/Lit/sec => Mol L-1 s-1
ROR = K [A]x [B]y
K = ROR
[A]x [B]y
Unit of K = Mol/Lit (⁖ x + y =
n)
Sec
[Mol/Lit]x [Mol/Lit]y
= [Mol/Lit/sec] => [Mol/Lit]1-n => [Mol/Lit]1-n

Unit of Order of Reaction
(n) & Rate Constant (K)
Order of Reaction (n) Unit of K [Mol/Lit]1-n /sec]
Zero order of reaction [Mol/Lit] /sec
First order of reaction sec-1
Second order of reaction [Mol/Lit]-1 /sec
Half order of reaction [Mol/Lit]3/2 /sec

K = 7 ˟ 10-4 Lit2 Mol-2 sec-1
[Mol/Lit]1-n /sec = [Mol/Lit]-2 /sec
1 – n = -2
Third order of reaction
Q. If rate constant is 7 ˟ 10-4 Lit2 Mol-2 sec-
1 of any chemical reaction. Find order of
reaction?

Q. 2A + 3B ----- 4C
If order of reaction with respect to A & B is 2 & -1. Write rate law
expression and calculate order of reaction? What is the effect on rate;
when,
(i). Concentration of A is doubled alone
(ii). Concentration of B is halved alone
(iii). Concentration of A & B is doubled
(iv). Volume of container increases 3 times
r = K [A]x [B]y
r = K [A]2 [B]-1
n = x + y
n = 2 + (-1) = 1 (First order of reaction)
K = sec-1
(i). r = K [A]2 [B]-1
r’ = K [2A]2 [B]-1
r’ = K [2A]2 [B]-1 => r’ = 22 => r’ = 4r
r K [A]2 [B]-1 r
Rate increases 4 times

Q. 2A + 3B ----- 4C
when,
(ii). r = K [A]2 [B]-1
r’ = K [A]2 [B/2]-1
r’ = K [2A]2 [B/2]-1 => r’ = 1 -1 => r’ = 2
r K [A]2 [B]-1 r 2 r
(iii). r = K [A]2 [B]-1
r’ = K [2A]2 [2B]-1
r’ = K [2A]2 [2B]-1 => r’ = (2)2 ˟ (2)-1 => r’ = 4 = 2
r K [A]2 [B]-1 r r 2

Q. 2A + 3B ----- 4C
when,
(iv). r = K [A]2 [B]-1
Volume α 1/Concentration
[A] = Number of Moles
Volume of Solution (in Lit)
Volume increase 3 times --- Concentration decreases 3 times
r = K [A]2 [B]-1
r’ = K [A/3]2 [B/3]-1
r’ = K [A/3]2 [B/3]-1 => r’ = [1/3]2 [1/3]-1 => r’ = 3
r K [A]2 [B]-1 r r 9
Rate decreases 3 times
(Due to number of moles per volume
=> Molarity)

Note:
1. Stoichiometric coefficients having nothing to do with order
2N2O5 -------- 4NO2 + O2
By Expt.: r = K [N2O5]1
2. In Rate law, concentration terms of products may be present
O3 --------- O2
By Expt.: r = K [O3]2 [O2]-1
3. In Rate law, concentration terms of some reactant may be present
NO2 + CO -------- NO + CO2
By Expt.: r = K [NO2]2 [CO]0 => r = K
[NO2]2

Note:
4. In Rate law expression, concentration term of catalyst may be present.
Catalyst ---- depend on reactant/product of reaction
2SO2 + O2 -------- 4SO3
By Expt.: r = K [O2]2 [NO]1
NO

Simple/ Elementary single
step reaction:
At slowest (single) step, -- Rate of Reaction -- Rate determined
3A + 2B -- C
Step1: 2A + B -- P
Step2: P + A -- Q
Step3: Q + B -- C
Final reaction: 3A + 2B -- C
By Expt.: r = K [A]2 [B]1
Example:
H2 + I2 ----- 2HI
r = K [H2]1 [I2]1
Single step Reaction
Guldbery & Wagge
Method
Law of Mass Action

Simple/ Elementary single
step reaction:
At slowest (single) step, -- Rate of Reaction -- Rate determined
3A + 2B -- C
Step1: 2A + B -- P
Step2: P + A -- Q
Step3: Q + B -- C
Final reaction: 3A + 2B -- C
By Expt.: r = K [A]2 [B]1
Example:
H2 + I2 ----- 2HI
r = K [H2]1 [I2]1
By Expt.: It’s not single step reaction
Single step Reaction
Guldbery & Wagge
Method
Law of Mass Action

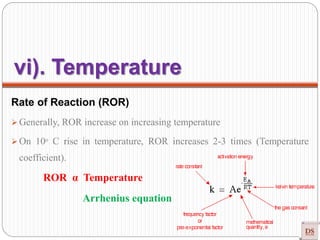
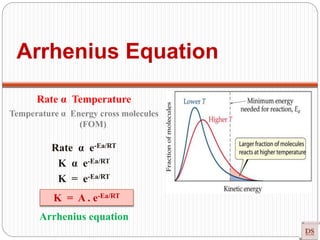
Arrhenius Equation
Effect of temperature on Rate of Reaction (ROR)
Rate α Temperature
Rate = K [conc]n
 Generally, ROR increases on increasing temperature (Approximately their
dependency of K on T)
 In most the reaction, when temperature increases 10ᵒC, ROR increases 2-3
times (Temperature coefficient).
r = K [A]x [B]y
r α K

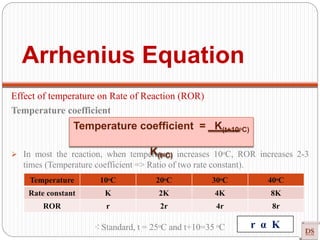
Arrhenius Equation
Effect of temperature on Rate of Reaction (ROR)
Temperature coefficient
 In most the reaction, when temperature increases 10ᵒC, ROR increases 2-3
times (Temperature coefficient => Ratio of two rate constant).
⁖ Standard, t = 25ᵒC and t+10=35 ᵒC
Temperature coefficient = K(t+10ᵒC)
K(tᵒC)
Temperature 10ᵒC 20ᵒC 30ᵒC 40ᵒC
Rate constant K 2K 4K 8K
ROR r 2r 4r 8r
r α K

Q. In a chemical reaction,
temperature coefficient is 5. if rate at
10ᵒC is x. find the rate constant at
70ᵒC?
Temper
ature
10ᵒC 20ᵒC 30ᵒC 40ᵒC 50ᵒC 60ᵒC 70ᵒC
Rate x 2x 4x 8x 16x 32x 64x
r α K

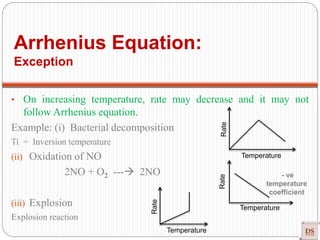
Arrhenius Equation:
Accurate dependency of ‘K’ on
‘T’
Arrhenius equation
[R = Universal gas constant = 8.314 joule/mole K]
Exponentially Increases
Rateconstant(K)
Temperature
(Joule/mole)
(constant)
(universal
constant)
(Kelvin)

Collision energy: when two chemicals react, their molecules have
to collide with each other (in a particular orientation) with
sufficient energy for the reaction to take place.
H2 + I2 ---- 2HI
For effective collision, (i) Orientation collision; and
(ii) Energy barrier
Arrhenius Equation:
‘T’

Arrhenius Equation:
‘T’
(i) Orientation collision:
Effective collision ----- Head to head collision
(ii) Energy barrier
Activation energy=
ER require energy to cross
the energy barrier to reach
At transition state
ER = ET - ER
Transition
state

K = A . e-Ea/RT
Rate α Temperature
Temperature α Energy cross molecules
(FOM)
Rate α e-Ea/RT
K α e-Ea/RT
K = e-Ea/RT
Arrhenius equation
Arrhenius Equation

K = A.e-Ea/RT
ln K = ln A + ln e-Ea/RT
ln K = ln A – Ea/RT logee
ln K = ln A – Ea/RT
y = mx + c
ln K = – Ea/R (1/T) + ln A
loge K = – Ea/R (1/T) + ln A (⁖loge K = 2.303 log10 K)
2.303 log10 K = 2.303 log10 A – Ea/RT
loge K = loge A – Ea/RT
Arrhenius Equation
log10 K = log10 A – Ea/2.303RT

If, K1 ------- T1; K2 ------- T2 (Assume T2 > T1)
log10 K1 = – Ea/2.303RT1 + log10 A -------- (i)
log10 K2 = – Ea/2.303RT2 + log10 A -------- (ii)
(Assume Ea & A are temperature independent)
Sub (ii) by (i)
log10 (K2 - K1) = Ea/2.303RT2 – Ea/2.303RT1
log10 (K2/K1) = Ea/2.303R (1/T1 - 1/T2)
log10 (K2/K1) = Ea/2.303R (T2 - T1/T1T2)
Arrhenius Equation:
Ratio of two rate constant at two different
temperature

Arrhenius Equation:
Exception
• On increasing temperature, rate may decrease and it may not
follow Arrhenius equation.
Example: (i) Bacterial decomposition
Ti = Inversion temperature
(ii) Oxidation of NO
2NO + O2 --- 2NO
(iii) Explosion
Explosion reaction
Temperature
Rate
Temperature
Rate
Temperature
Rate
- ve
temperature
coefficient

Mechanism of
Reaction
On the basis of mechanism we have two types of
reactions:
(i) Simple / elementary / single type / single step
reaction
(ii) Complex / multistep reaction
Fast reaction
Slow reaction
Moderate reaction

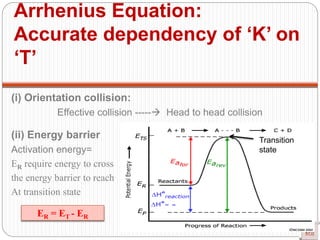
Single step reaction
2A + 2B -------- 3AB
A-------A B--------B a------b
•There is no intermediate
•Activation energy:
Rate law: r = K [A] [B]
Experimentally method
Guldberg and Wagge method : Law of mass action

1. H2 + I2 ------ 2HI
Reactant ------ Product
A ----- PRODUCT
Molecularity = 1 (Molecules in reactant)
r = K [A]
2. A + B ------ > PRODUCT
Molecularity = 2
r = K [A] [B]

3. A + 2B ---- Product
Molecularity = 3
r = K [A] [B]
Maximum molecularity ===== single step reaction
• Simultaneous collision
• Proper collision
• Cross energy barrier

Complex step reaction
Multi step reaction:
R -------- P
R - A
A- B
B - P
R - P
• There is intermediate
• Such reactions occurs in several steps, where each steps is elementary
• Molecularity of complex reaction is not define
Molecularity of each step can be defined
• Over all rate is given by slowest step of complex reaction --- rate
determining step (rds) ------ slowest step

Sharma’s Classes - Dr. Divya Sharma

Chemical Kinetics

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to Chemical Kinetics

Similar to Chemical Kinetics (20)

More from A Biodiction : A Unit of Dr. Divya Sharma

More from A Biodiction : A Unit of Dr. Divya Sharma (20)

Recently uploaded

Recently uploaded (20)

Chemical Kinetics