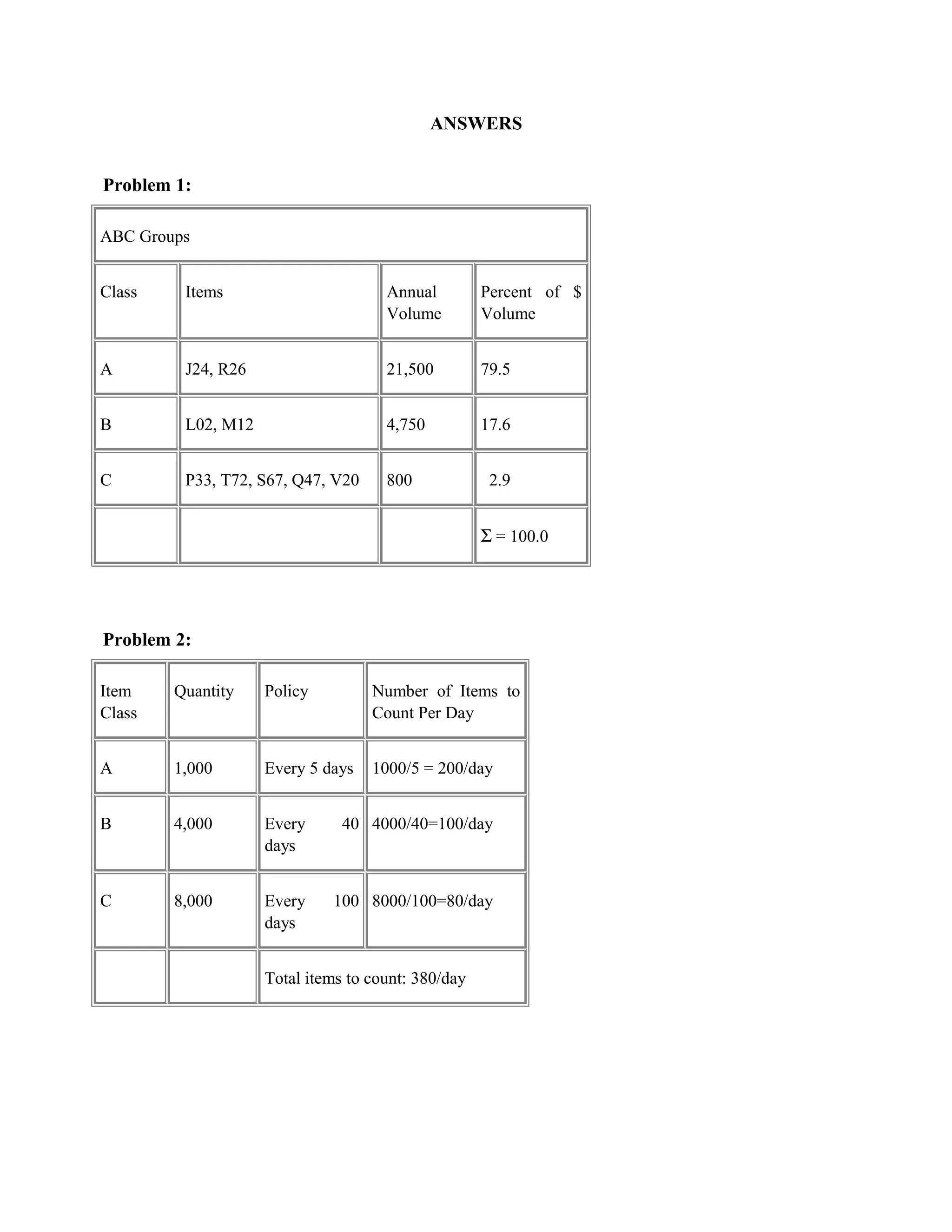
The document contains practice problems related to inventory management. Problem 1 involves classifying inventory items into ABC categories based on annual dollar volume. Problems 2-5 calculate order quantities, order frequencies, and total costs for inventory items. Problems 6-11 involve calculations related to safety stock, reorder points, economic order quantities, and inventory policies under different demand assumptions.

1. Practice Problems: Chapter 12, Inventory Management
Problem 1:
ABC Analysis
Stock Number
Annual
$
Volume
Percent of Annual $
Volume
J24
12,500
46.2
R26
9,000
33.3
L02
3,200
11.8
M12
1,550
5.8
P33
620
2.3
T72
65
0.2
S67
53
0.2
Q47
32
0.1
V20
30
0.1
Σ = 100.0
What are the appropriate ABC groups of inventory items?

2. Problem 2:
A firm has 1,000 “A” items (which it counts every week, i.e., 5 days), 4,000 “B” items (counted
every 40 days), and 8,000 “C” items (counted every 100 days). How many items should be counted
per day?
Problem 3:
Assume you have a product with the following parameters:
Demand = 360
Holding cost per year = $1.00 per unit
Order cos t: = $100 per order
What is the EOQ?
Problem 4:
Given the data from Problem 3, and assuming a 300-day work year; how many orders should be
processed per year? What is the expected time between orders?
Problem 5:
What is the total cost for the inventory policy used in Problem 3?
Problem 6:
Assume that the demand was actually higher than estimated (i.e., 500 units instead of 360 units).
What will be the actual annual total cost?
Problem 7:
If demand for an item is 3 units per day, and delivery lead-time is 15 days, what should we use for
a re-order point?
Problem 8:
Assume that our firm produces type C fire extinguishers. We make 30,000 of these fire
extinguishers per year. Each extinguisher requires one handle (assume a 300 day work year for
daily usage rate purposes). Assume an annual carrying cost of $1.50 per handle; production setup
cost of $150, and a daily production rate of 300. What is the optimal production order quantity?

3. Problem 9:
We need 1,000 electric drills per year. The ordering cost for these is $100 per order and the
carrying cost is assumed to be 40% of the per unit cost. In orders of less than 120, drills cost $78;
for orders of 120 or more, the cost drops to $50 per unit.
Should we take advantage of the quantity discount?
Problem 10:
Litely Corp sells 1,350 of its special decorator light switch per year, and places orders for 300 of
these switches at a time. Assuming no safety stocks, Litely estimates a 50% chance of no shortages
in each cycle, and the probability of shortages of 5, 10, and 15 units as 0.2, 0.15, and 0.15
respectively. The carrying cost per unit per year is calculated as $5 and the stockout cost is
estimated at $6 ($3 lost profit per switch and another $3 lost in goodwill, or future sales loss). What
level of safety stock should Litely use for this product? (Consider safety stock of 0, 5, 10, and 15
units)
Problem 11:
Presume that Litely carries a modern white kitchen ceiling lamp that is quite popular. The
anticipated demand during lead time can be approximated by a normal curve having a mean of 180
units and a standard deviation of 40 units. What safety stock should Litely carry to achieve a 95%
service level?

4. ANSWERS
Problem 1:
ABC Groups
Class
Items
Annual
Volume
Percent of $
Volume
A
J24, R26
21,500
79.5
B
L02, M12
4,750
17.6
C
P33, T72, S67, Q47, V20
800
2.9
Σ = 100.0
Problem 2:
Item
Class
Quantity
Policy
Number of Items to
Count Per Day
A
1,000
Every 5 days
1000/5 = 200/day
B
4,000
Every
days
40 4000/40=100/day
C
8,000
Every
days
100 8000/100=80/day
Total items to count: 380/day

5. Problem 3:
EOQ =
2 * Demand * Order cost
=
Holding cost
2 * 360 * 100
= 72000 = 268 items
1
Problem 4:
N=
Demand 360
=
= 134 orders per year
.
Q
268
T=
Working days
= 300 / 1.34 = 224 days between orders
Expected number of orders
Problem 5:
TC =
Demand * Order Cost (Quantity of Items) * ( Holding Cost ) 360 * 100 268 * 1
+
=
+
= 134 + 134 = $268
Q
2
268
2
Problem 6:
TC =
Demand * Order Cost (Quantity of Items) * ( Holding Cost ) 500 * 100 268 * 1
+
=
+
= 186.57 + 134 = $320.57
Q
2
268
2
Note that while demand was underestimated by nearly 50%, annual cost increases by only 20%
(320 / 268 = 1.20) an illustration of the degree to which the EOQ model is relatively insensitive to
small errors in estimation of demand.
Problem 7:
ROP = Demand during lead - time = 3 * 15 = 45 units
Problem 8:
Q* =
p
2 * Demand * Order Cost
=
Daily Usage Rate
Holding Cost 1 −
Daily Pr oduction Rate
Problem 9:
F
G
H
I
J
K
( 2)(30,000)(150)
= 3000 units
100
150 1 −
.
300
F I
G J
H K

6. Q* ($78) =
p
(2)(1000)(100)
= 80 units
(0.4)(78)
Q* ($50) =
p
(2)(1000)(100)
= 100 units = 120 to take advantage of quantity discount.
(0.4)(50)
Ordering 100 units at $50 per unit is not possible; the discount does not apply until 120 the order
equals 120 units. Therefore, we need to compare the total costs for the two alternatives.
Demand * Order Cost ( Quantity of Items) * ( Holding cos t )
+
Q
2
Total cos t = Demand * Cost +
Total cos t ($78) = (1000)(78) +
(1000)(100) (80)(0.4)(78)
+
= $80,498
80
2
Total cos t ($50) = (1000)(50) +
(1000)(100) (120)( 0.4)(50)
+
= $52,033
120
2
Therefore, we should order 120 each time at a unit cost of $50 and a total cost of $52,033.
Problem 10:
Safety stock = 0 units:
Carrying cost equals zero.
Stockout cos ts = (Stockout cos t * possible units of shortage * probability of shortage * number of orders per year )
S0 = 6 * 5* 0.2 *
1350
1350
1350
+ 6 * 10 * 015*
.
+ 6* 15* 015*
.
= $128.25
300
300
300
Safety stock = 5 units:
Carrying cos t = $5 per unit * 5 units = $25
.
Stockout cost: S5 = 6* 5* 015*
1350
1350
+ 6 * 10 * 015*
.
= $60.75
300
300

7. Total cos t = carrying cos t + stockout cos t = $25 + $60.75 = $85.75
Safety stock = 10 units:
Carrying cos t = 10 * 5 = $50.00
.
Stockout cost: S10 = 6* 5* 015*
1350
= $20.25
300
Total cos t = carrying cos t + plus stockout cos t = $50.00 + $20.25 = $70.25
Safety stock = 15:
Carrying cos t = 15* 5 = $75.00
Stockout cos ts = 0 (there is no shortage if 15 units are maintained)
Total cos t = carrying cos t + stockout cos t = $75.00 + $0 = $75.00
Therefore: Minimum cost comes from carrying a 10-unit safety stock.
Problem 11:
To find the safety stock for a 95% service level it is necessary to calculate the 95th percentile on
the normal curve. Using the standard Normal table from the text, we find the Z value for 0.95 is
1.65 standard units. The safety stock is then given by:
(165* 40) + 180 = 66 + 180 = 246 Ceiling Lamps
.