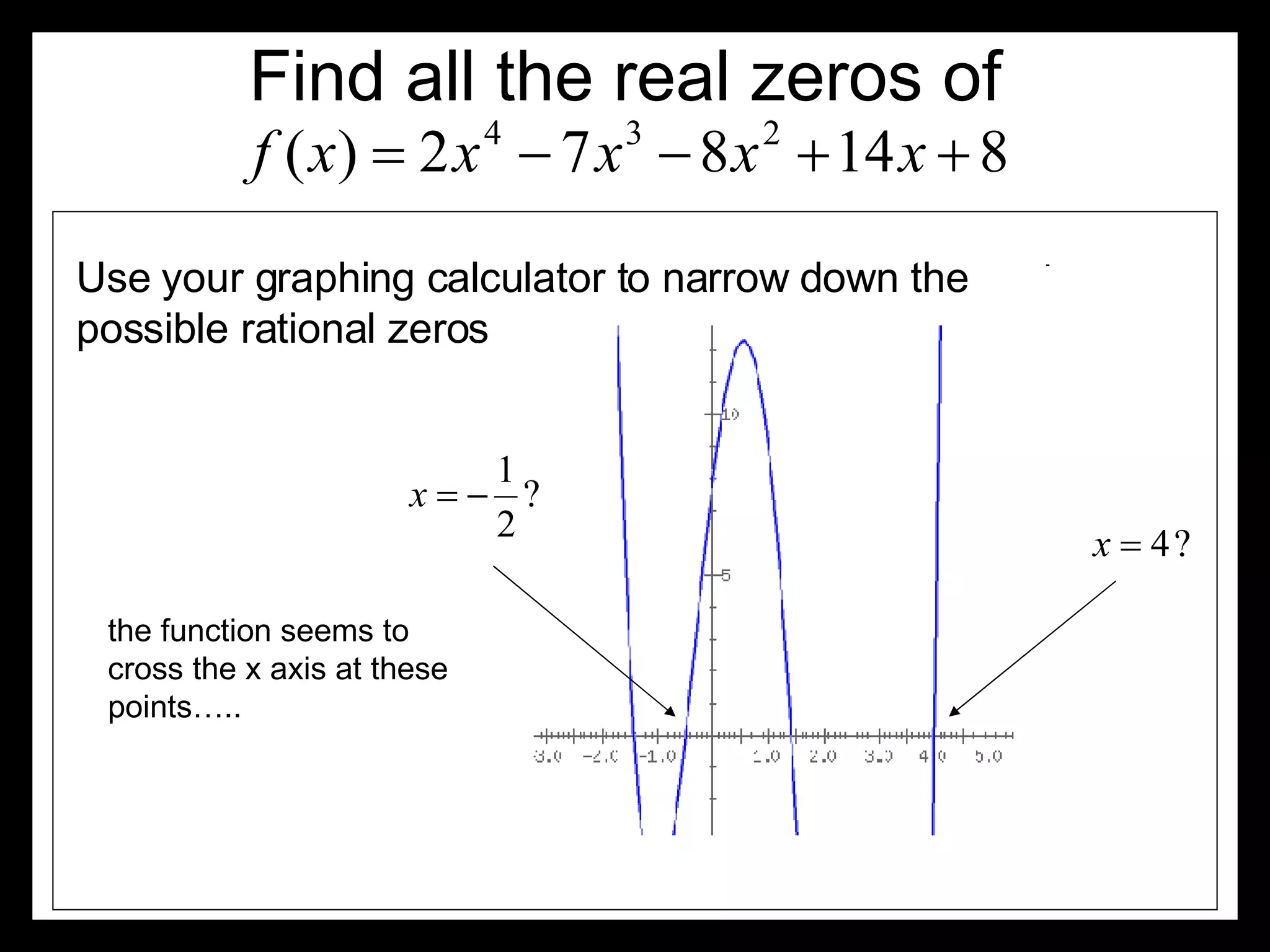
The document discusses finding all real zeros of a polynomial function. It outlines the steps to take: 1) Use the Rational Zeros Theorem to identify possible rational zeros. 2) Use a graphing calculator to narrow down possible rational zeros by identifying where the function crosses the x-axis. 3) Use synthetic division and factoring techniques to rewrite the polynomial in factored form. 4) Identify the real zeros by finding where each factor equals zero.

1. Finding all real zeros of a Polynomial

2. Find all the real zeros of Use the Rational Zeros Theorem to make a list of possible rational zeros

3. Find all the real zeros of Use your graphing calculator to narrow down the possible rational zeros the function seems to cross the x axis at these points…..

4. Find all the real zeros of Use the remainder and factor theorems to test the possible zeros since the remainder is zero, x + ½ is a factor! since the remainder is zero, x - 4 is a factor!

5. Find all the real zeros of Use one of the divisors to divide the dividend Let’s start with (x - 4) So the dividend is equal to: 4 2 -7 -8 14 8 2 1 -4 -2 0 8 4 -16 -8

6. Find all the real zeros of Now, let’s use the other factor of (x + ½) to divide the second factor: So the dividend is equal to: Which means our original function is equal to: -1 0 2 2 1 -4 -2 2 0 -4 0

7. Find all the real zeros of Synthetic division has allowed us to factor most of this polynomial, but now we can use other factor techniques to take care of the rest! Factor out the GCF And then use difference of two squares method to factor one last time

8. Find all the real zeros of Now that you have the polynomial in factored form, find those zeros!!! discard the constant Zeros: SOLUTION!!! So the zeros of f are the rational numbers 4 and -1/2 and the irrational numbers are and

9. Re-Cap of the Process Use Rational Zeros Theorem to locate possible zeros Use Calculator to narrow down possible zeros Use Synthetic Division to rewrite the function as (divisor)(quotient) Repeat Synthetic Division of quotient until you can factor the remaining quotient Use the Zero Product Property to find all real zeros