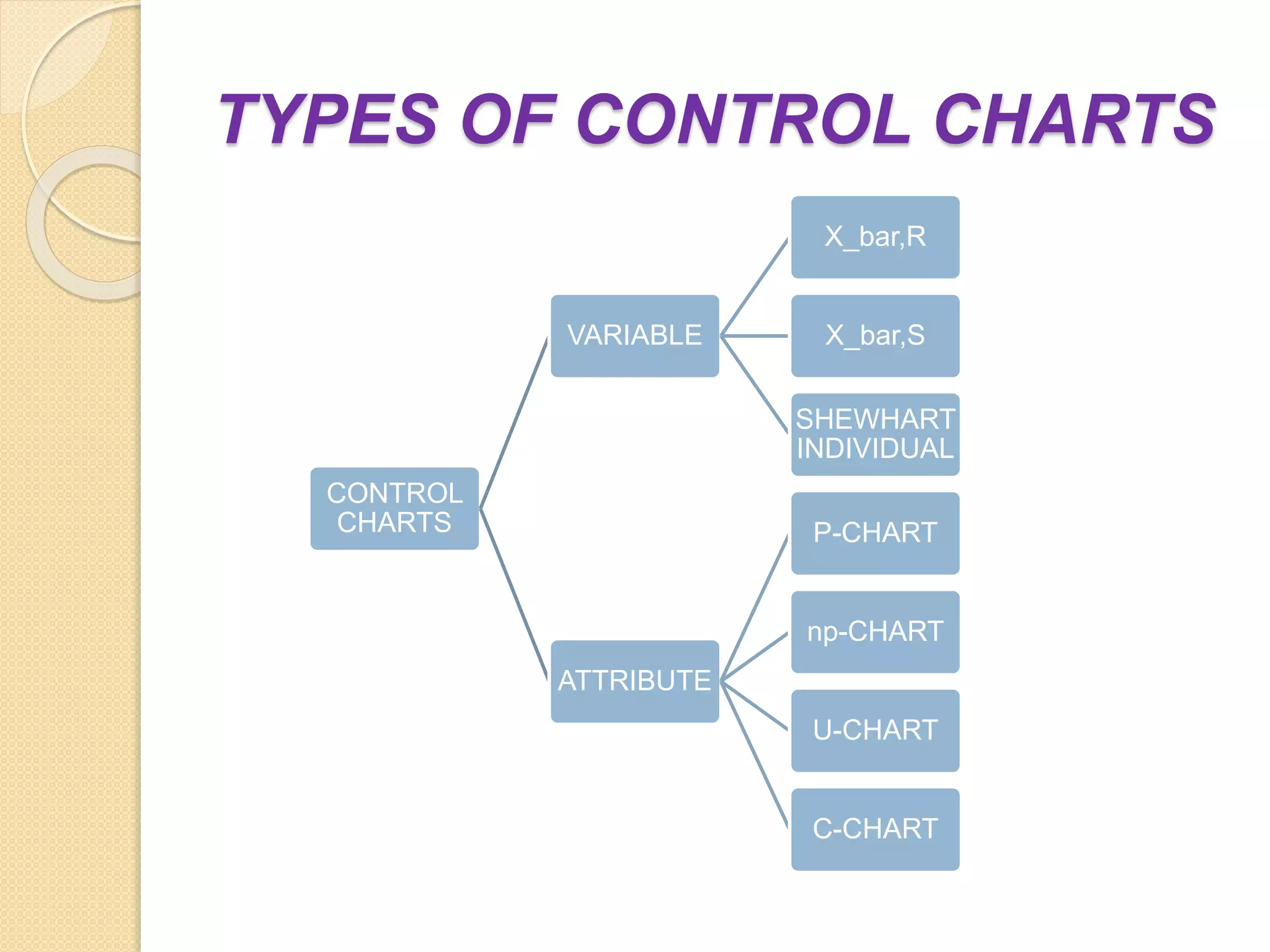
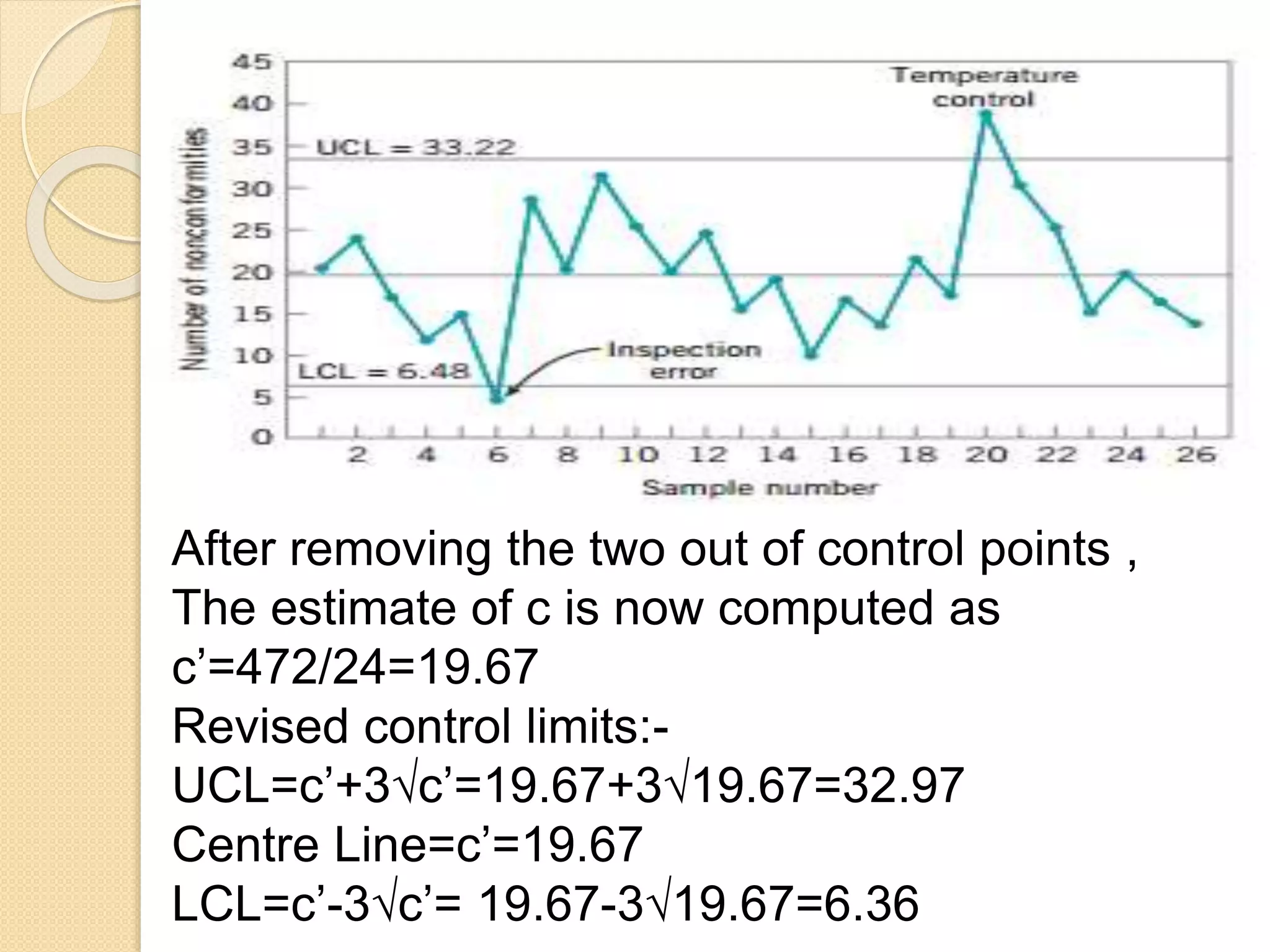
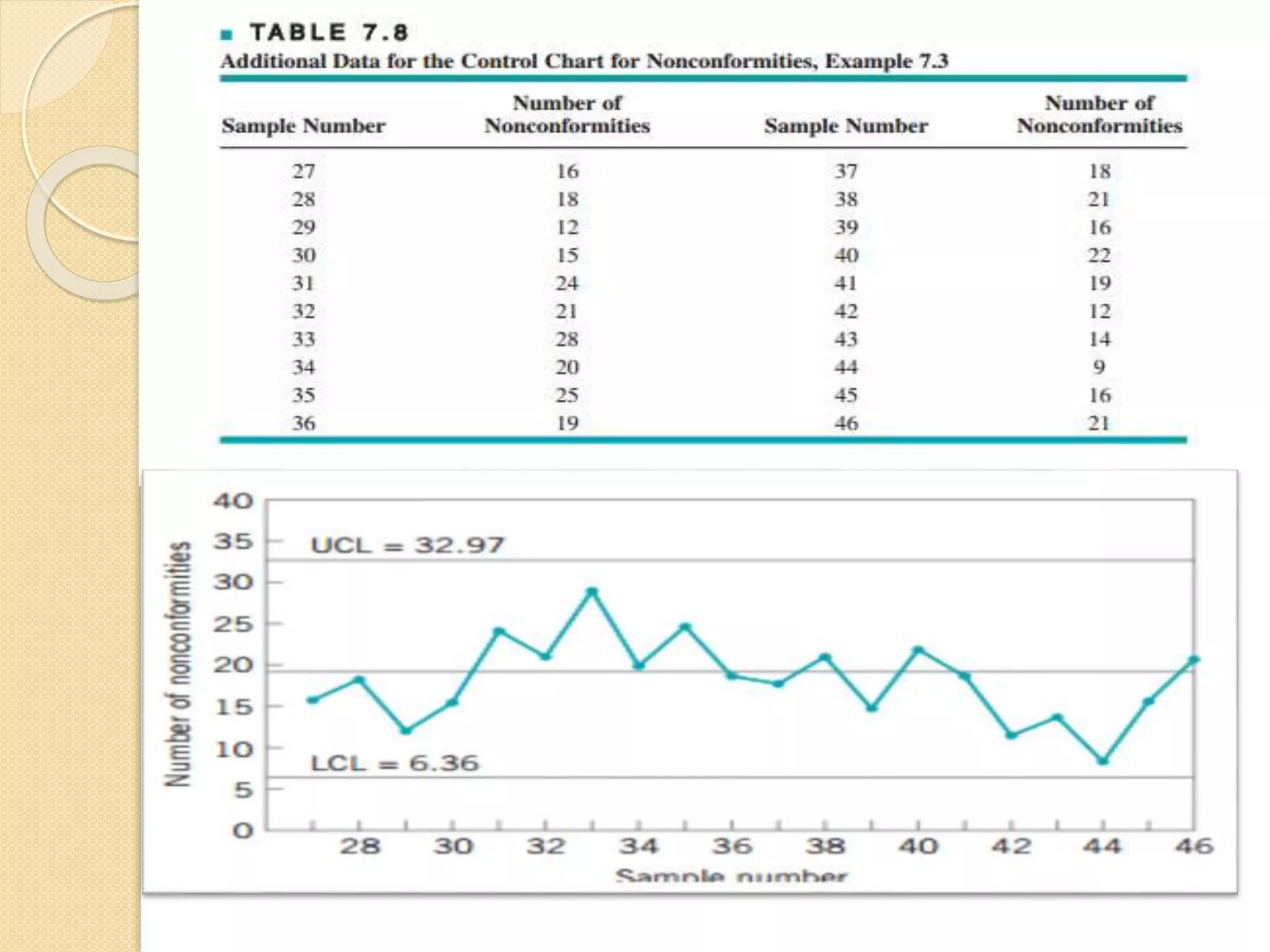
This document discusses control charts, specifically the C-chart. It defines a C-chart as a control chart used for nonconformities, or defects, in a product. A C-chart graphs the total number of nonconformities found in samples versus the sample number. It contains a central line at the expected value of defects (c) and upper and lower control limits at c ± 3√c. The document provides an example of constructing a C-chart using sample data and outlines how C-charts can be used in healthcare processes to monitor quality.

1. PRESENTED BY
RITUPARNA GHOSH
APRAJIT JHA
M.Sc BIOSTATISTICS AND DEMOGRAPHY

2. BASIC PRINCIPLES OF
CONTROL CHARTS
 The control chart is a graphical display
of a quality characteristic that has
been measured or computed from a
sample versus the sample number or
time.
 The charts contains a central line,a
upper control limit and a lower control
limit.

3. TYPES OF CONTROL CHARTS
CONTROL
CHARTS
VARIABLE
X_bar,R
X_bar,S
SHEWHART
INDIVIDUAL
ATTRIBUTE
P-CHART
np-CHART
U-CHART
C-CHART

4. HEALTHCARE & CONTROL
CHART
 Control chart
Aid in process understanding
Assess process stability
Identify changes indicating improvement
or
deteoriation in quality
 Used in
Hospital process improvement projects
Accrediting bodies and governmental
agencies
Public health surveillance

5. CONTROL CHART FOR
NONCONFORMITIES(DEFECT)
 The nonconfirming item is a unit of
product that doesnt satisfy the
specifications for that product.
 Distinction between a defect and
defective is clear
 Defect:-Any instance of the item’s
lack of conformity to specification.
 Defective:-Item that fails to fulfil one
or more of the given specifications

6. WHAT IS C-CHART?
 Originally proposed by Walter A.
Shewhart.
 It is a control chart for
nonconformities.
 Developed for total number of
nonconformities in a unit.
 Underlying distribution-Poisson
distribution.
 Two cases- 1.Standard given.
2.Standard not given.

7. C-CHART:STANDARD GIVEN
 UCL =c+3√c.
 Central line= c
 LCL=c-3√c.
NOTE:
where c is the parameter of Poisson
distribution.
If LCL comes negative, take it as 0.

8. C-CHART:STANDARD NOT
GIVEN
Let ci be the c value for the sample taken
from the ith subgroup(i=1(1)n).Then the
appropriate estimate of c will be
c’=∑ ci /n.
 UCL= c’+3√c’.
 CENTRAL LINE= c’.
 LCL= c’-3√c’.

9. NOTE:
c’ is the estimated value of the
poisson parameter. c’ may be estimated
as the observed average number of
nonconformities in a preliminary sample
of inspection units.
When no standard is given, the control
limits in equation should be regarded as
trial control limits.

10. 26 Samples -516 total nonconformities
c’=516/26=19.85
UCL=c’+3√c’=19.85+3√19.85=33.22
Centre Line=c’=19.85
LCL=c’-3√c’=19.85-3√19.85=6.48
EXAMPLE…

11. After removing the two out of control points ,
The estimate of c is now computed as
c’=472/24=19.67
Revised control limits:-
UCL=c’+3√c’=19.67+3√19.67=32.97
Centre Line=c’=19.67
LCL=c’-3√c’= 19.67-3√19.67=6.36

13. Interpretation
The process is under control.
No lack of control is indicated.

14. USE OF C-CHART IN HEALTH
CARE
 Attribute data involves-
-counts(no.of falls per day).
--proportions(proportion of patients
receiving right antibiotics).
-rate(the number of falls per 1000
patient-days).
• For counts we use c-chart.

15. CONCLUSION
 Defect or nonconformity data are always
more informative than fraction
nonconforming,
 Widely used in transactional and service
business applications of statistical
process control.
 The limitation of c chart is that it takes
samples of constant size where in reality
it might not be so.In case of variable
sample size we use the u charts that
gives us the no.of defects per unit i.e
u=c/n.

16. SOURCES
 “Introduction to StatisticalQualityControl”-Doughlas
C.Montgomery
 “Fundamentalsof StatisticsVol-2”-
A.M.Gun,M.K.Gupta,B.Dasgupta
 support.minitab.com/en-us/minitab/17/topic-
library/quality-tools/control-charts/understanding-
attributes-control-charts/what-is-a-c-chart/
 http://www.coe.neu.edu/healthcare/pdfs/publications
/C13-Use_of_Control_C.pdf.