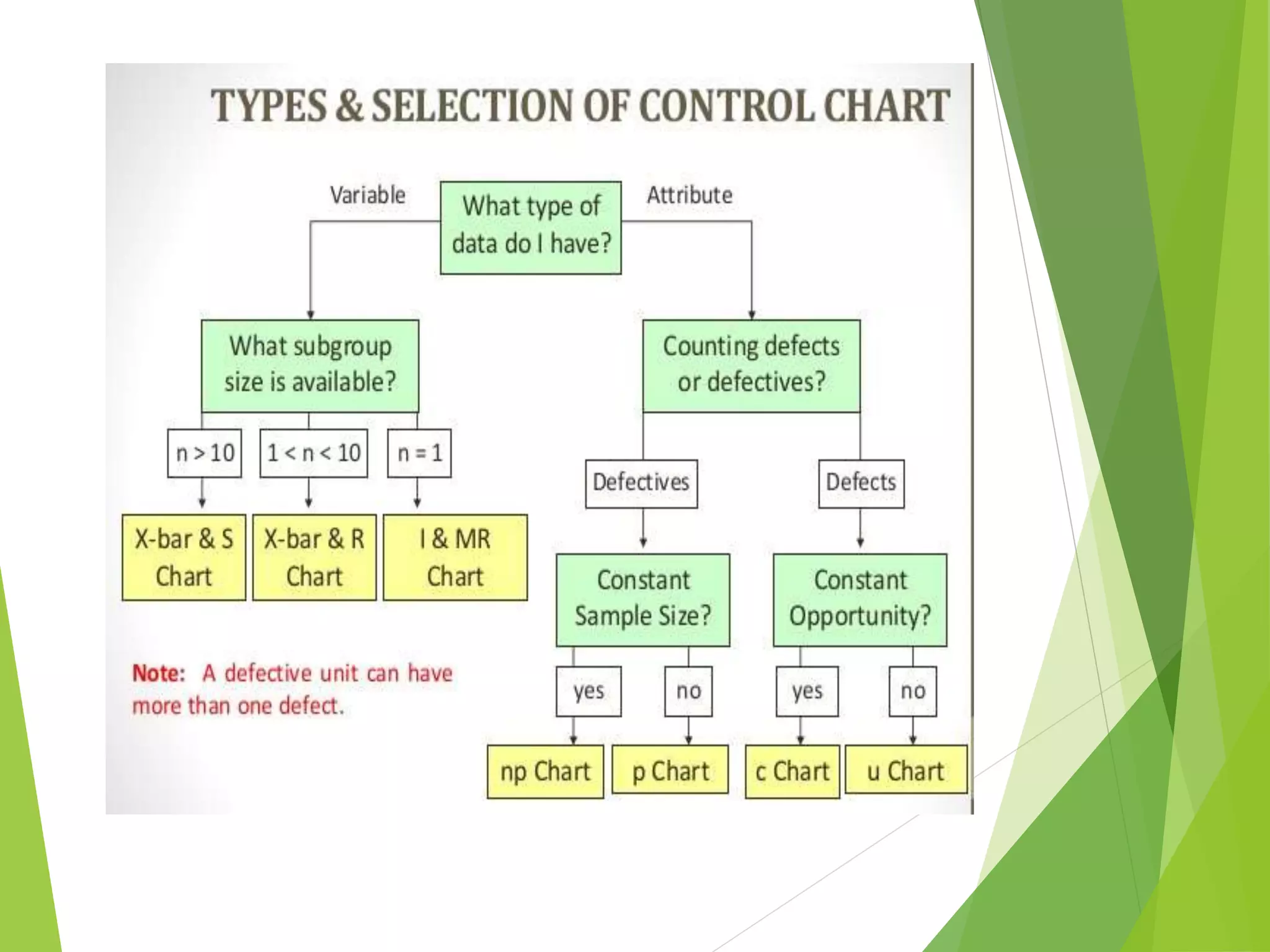
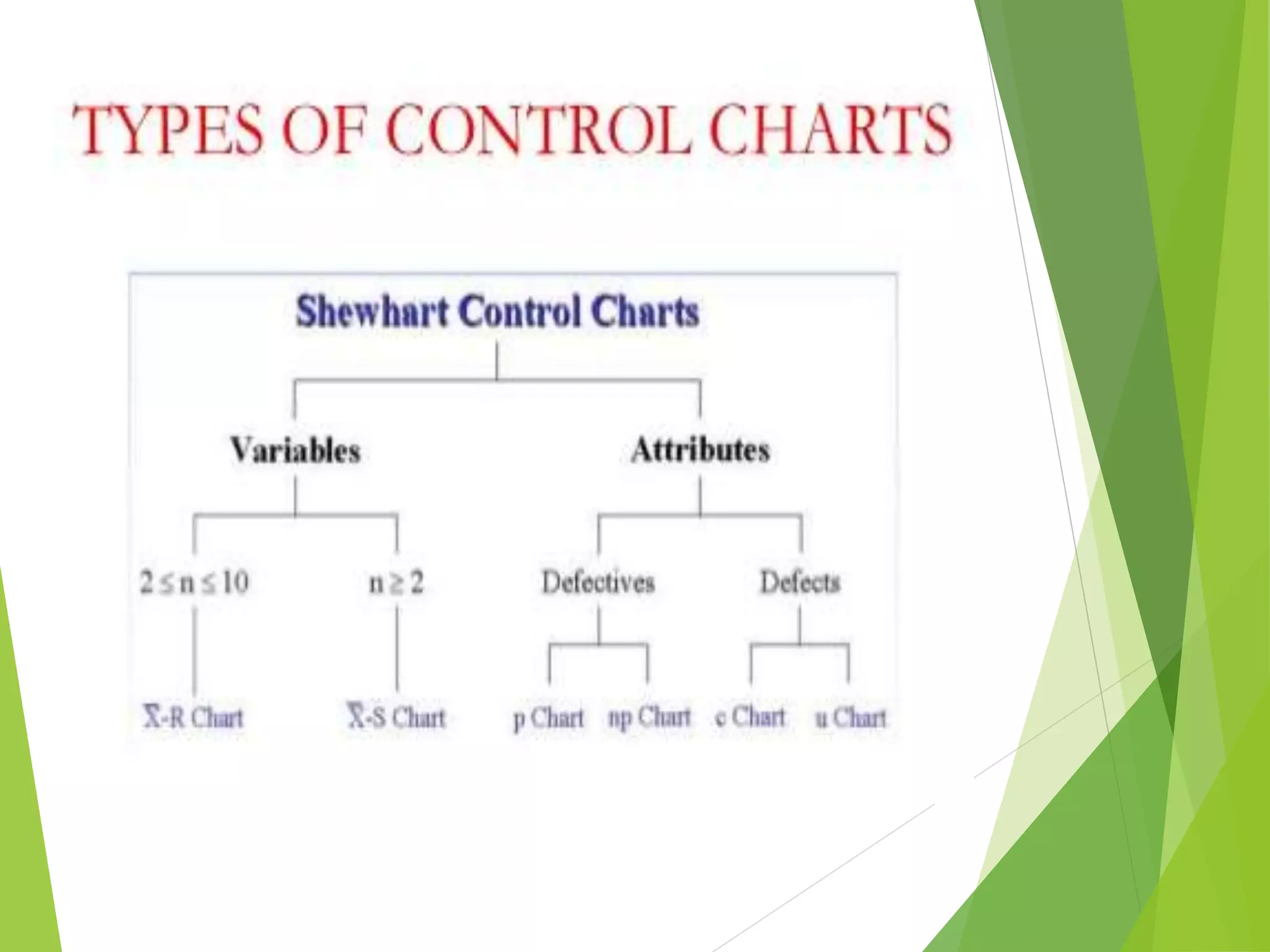
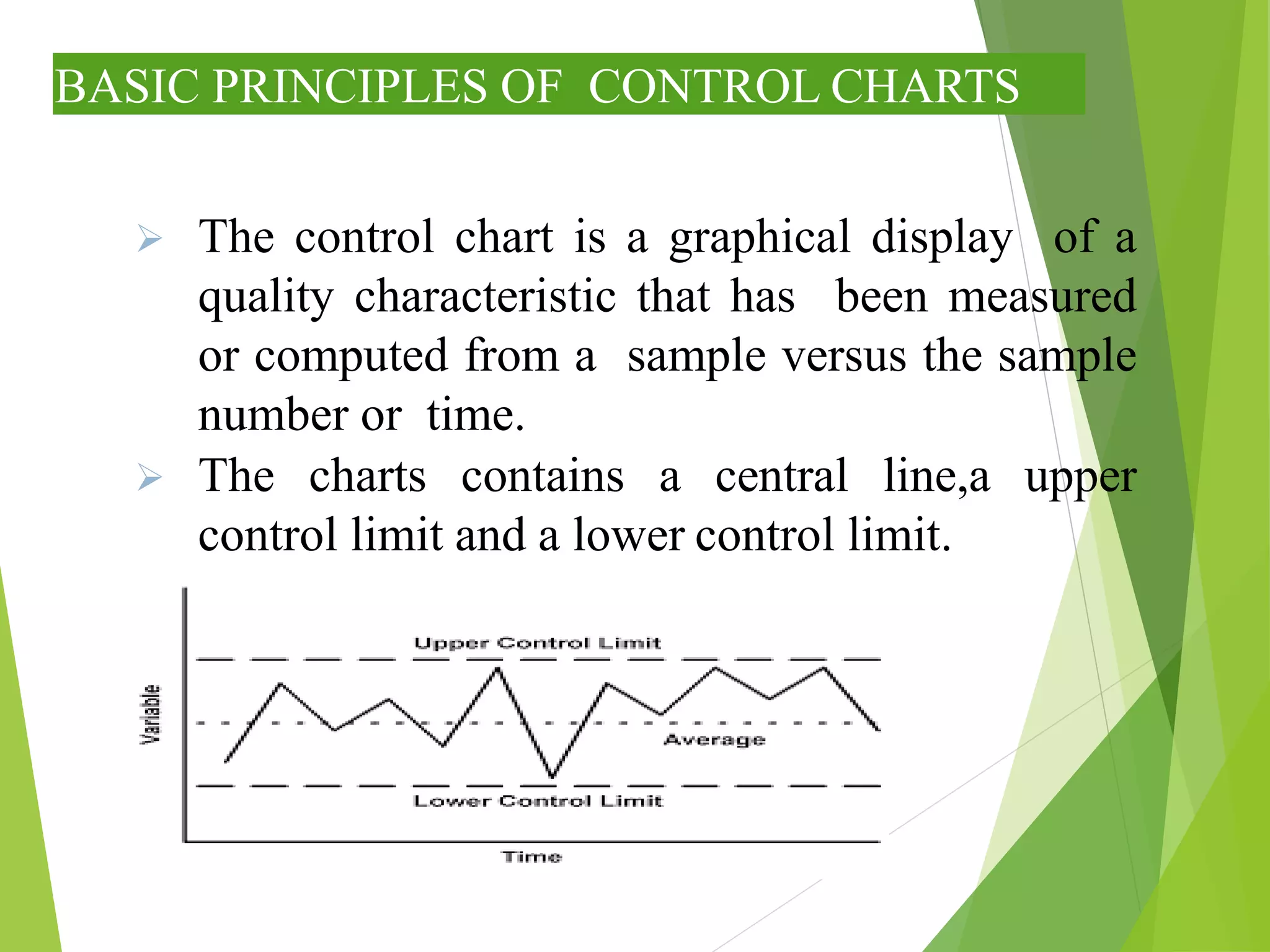
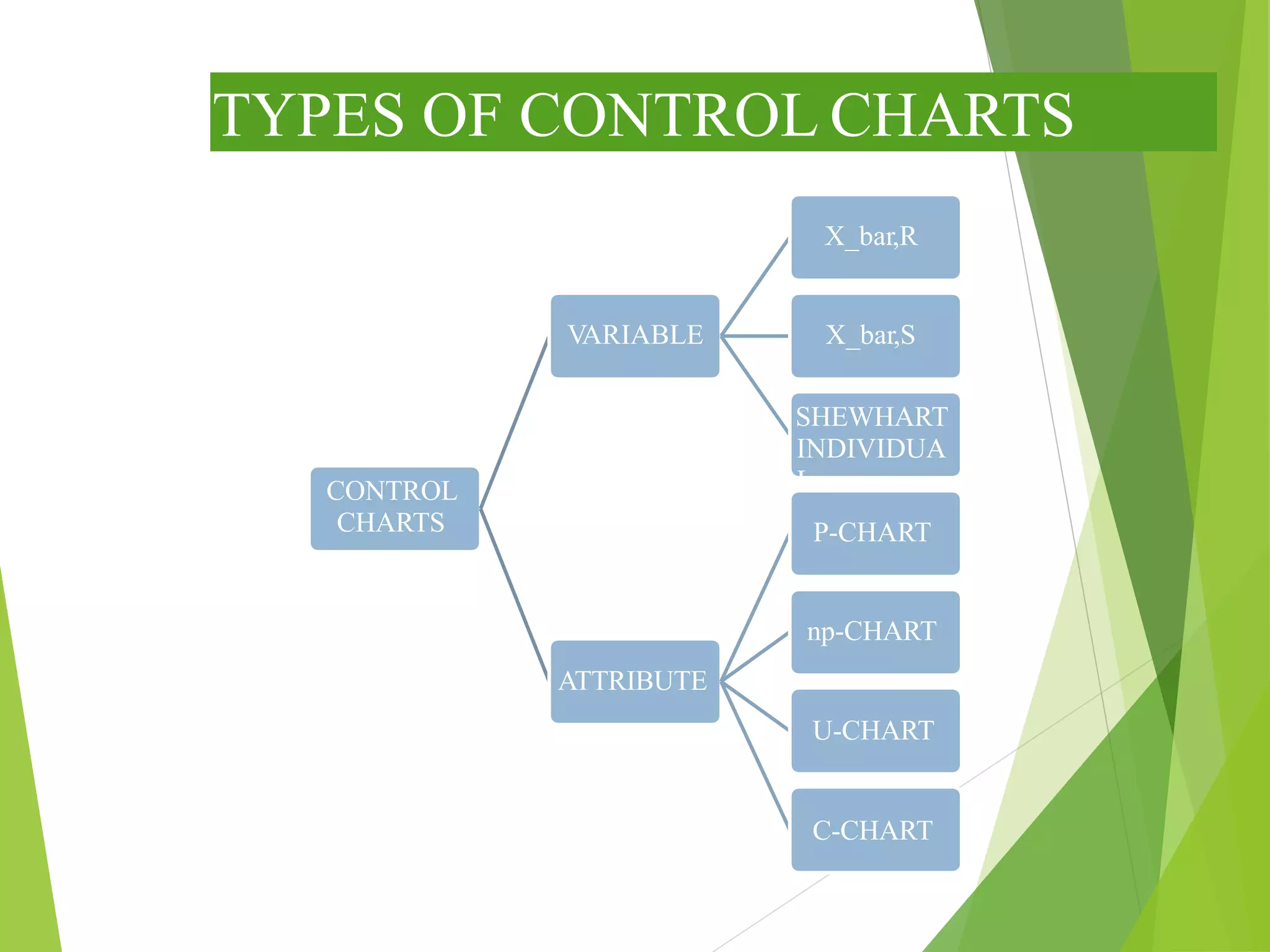
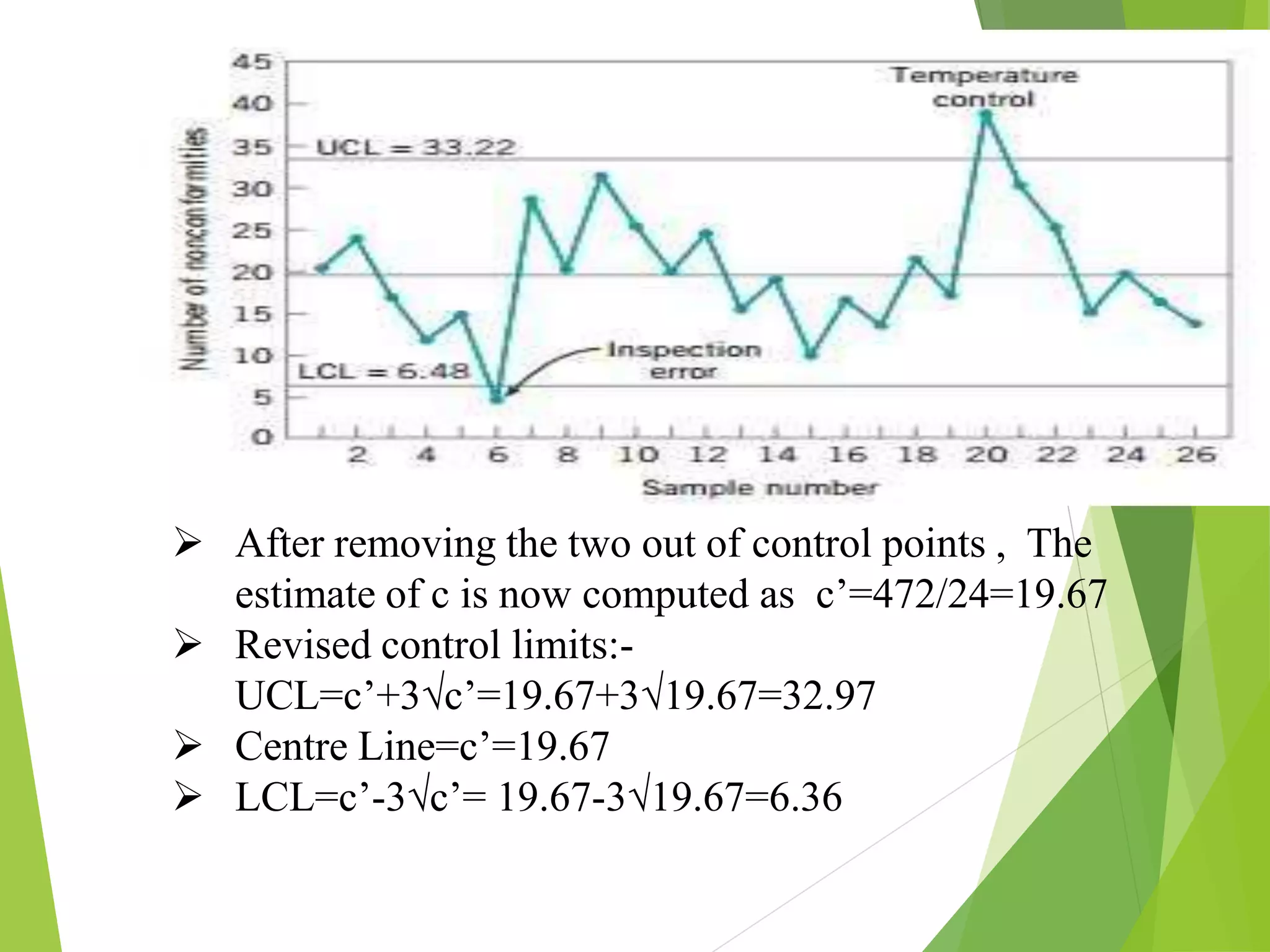
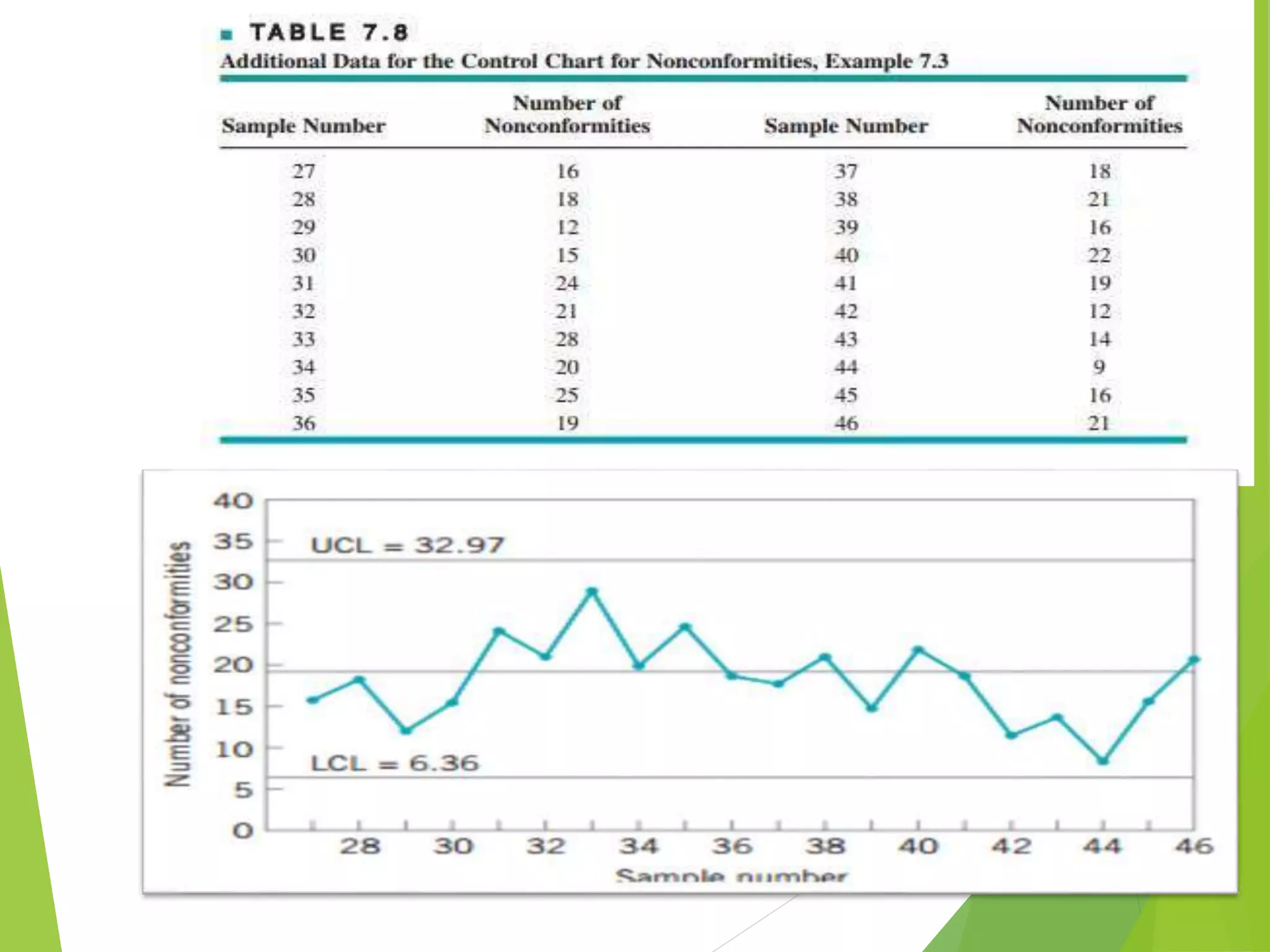
This document discusses C-charts, which are control charts used for nonconformities. C-charts can be used when a standard for nonconformities is given or not given. The chart contains an upper control limit, center line, and lower control limit. C-charts follow a Poisson distribution and are useful for healthcare process improvement and quality control. Examples are provided to demonstrate how to calculate control limits for a C-chart.

1. Work Study -Basic procedure involved in Method
Study and Work Measurement-Statistical Quality
Control :C CHART:
Mr.Bestha Chakrapani M.pharm (Ph.D)
Associate Professor
Department of Pharmaceutical sciences
Balaji college of Pharmacy
Anantapuramu
UNIT–II

2. C CHART

8. BASIC PRINCIPLES OF CONTROL CHARTS
 The control chart is a graphical display of a
quality characteristic that has been measured
or computed from a sample versus the sample
number or time.
 The charts contains a central line,a upper
control limit and a lower control limit.
.

9. TYPES OF CONTROL CHARTS
CONTROL
CHARTS
VARIABLE
X_bar,R
X_bar,S
SHEWHART
INDIVIDUA
L
P-CHART
np-CHART
ATTRIBUTE
U-CHART
C-CHART

10. HEALTHCARE & CONTROL CHART
 Control chart
Aid in process understanding
Assess process stability
Identify changes indicating improvement or
deteoriation in quality
 Used in
Hospital process improvement projects
Accrediting bodies and governmental
agencies
Public health surveillance

11. CONTROL CHART FOR
NONCONFORMITIES(DEFECT)
 The nonconfirming item is a unit of
product that doesnt satisfy the
specifications for that product.
 Distinction between a defect and
defective is clear
 Defect:-Any instance of the item’s
lack of conformity to specification.
 Defective:-Item that fails to fulfil one
or more of the given specifications

12. WHAT IS C-CHART?
 Originally proposed by WalterA.
Shewhart.
 It is a control chart for
nonconformities.
 Developed for total number of
nonconformities in a unit.
 Underlying distribution-Poisson
distribution.
 Two cases- 1.Standard given.
2.Standard not given.

13. C-CHART:STANDARD GIVEN
 UCL =c+3√c.
 Central line= c
 LCL=c-3√c.
NOTE:
where c is the parameter of Poisson
distribution.
If LCL comes negative, take it as 0.

14. C-CHART:STANDARD NOT GIVEN
Let ci be the c value for the sample taken
from the ith subgroup(i=1(1)n).Then the
appropriate estimate of c will be
c’=∑ ci /n.
 UCL= c’+3√c’.
 CENTRAL LINE= c’.
 LCL= c’-3√c’.

15. NOTE:
c’ is the estimated value of the poisson
parameter. c’ may be estimated as the
observed average number of
nonconformities in a preliminary sample of
inspection units.
When no standard is given, the control
limits in equation should be regarded as trial
control limits.

16. 26 Samples -516 total nonconformities
c’=516/26=19.85
UCL=c’+3√c’=19.85+3√19.85=33.22
Centre Line=c’=19.85
LCL=c’-3√c’=19.85-3√19.85=6.48
EXAMPLE…

17.  After removing the two out of control points , The
estimate of c is now computed as c’=472/24=19.67
 Revised control limits:-
UCL=c’+3√c’=19.67+3√19.67=32.97
 Centre Line=c’=19.67
 LCL=c’-3√c’= 19.67-3√19.67=6.36

19. USE OF C-CHART IN HEALTH CARE
 Attribute data involves-
 -counts(no.of falls per day).
 --proportions(proportion of patients receiving right antibiotics).
-rate(the number of falls per 1000 patient-days).
 For counts we use c-chart.

20. CONCLUSION
 Defect or nonconformity data are always
more informative than fraction
nonconforming,
 Widely used in transactional and service
business applications of statistical process
control.
 The limitation of c chart is that it takes
samples of constant size where in reality it
might not be so.In case of variable sample
size we use the u charts that gives us the
no.of defects per unit i.e u=c/n.