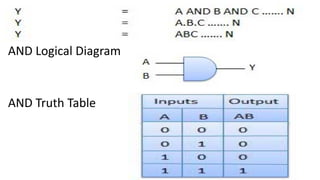
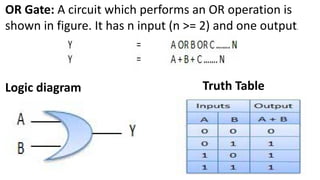
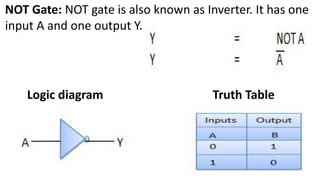
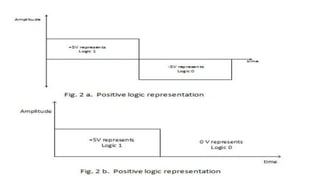
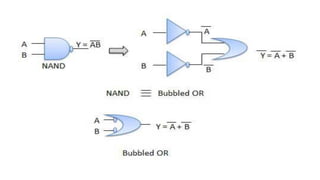
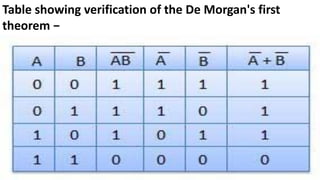
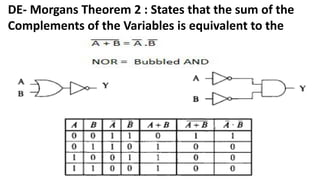
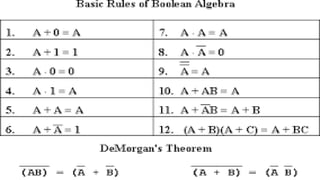
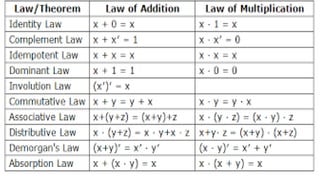
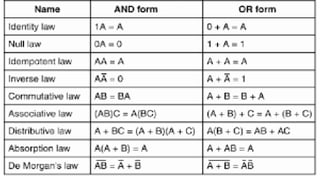
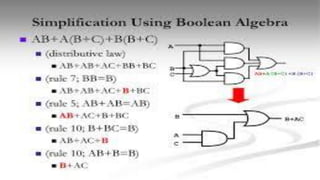
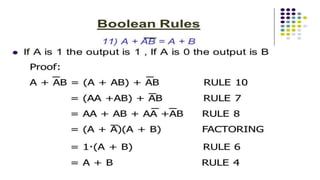
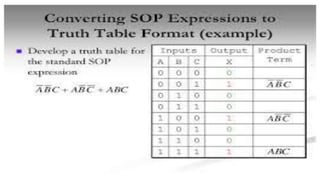
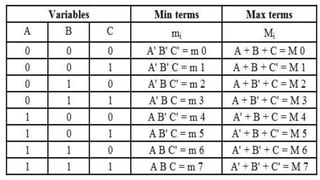
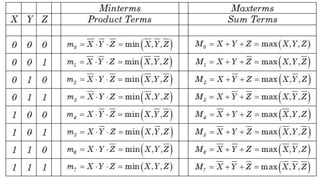
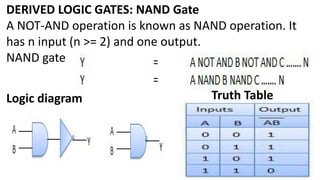
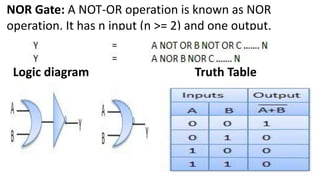
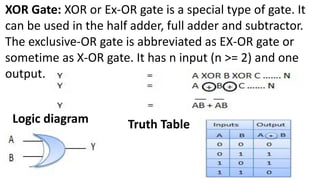
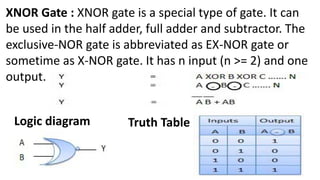
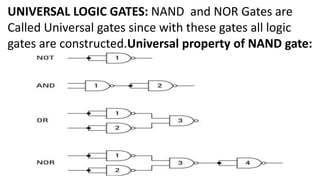
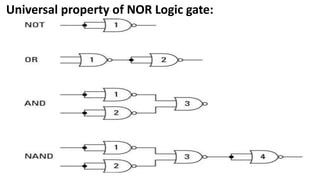
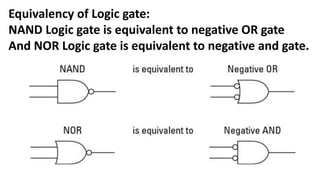
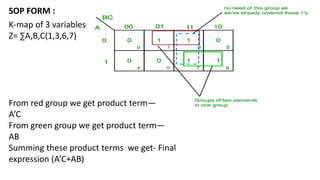
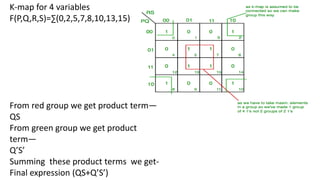
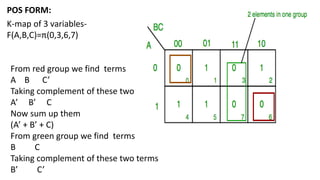
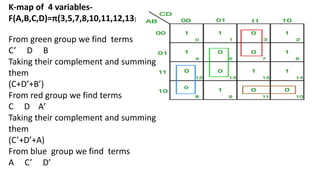
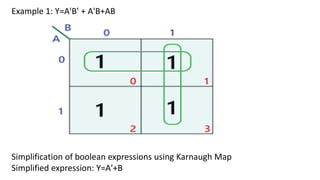
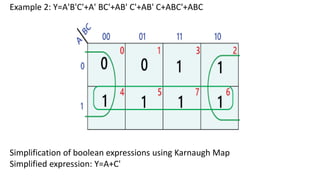
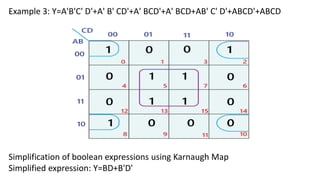
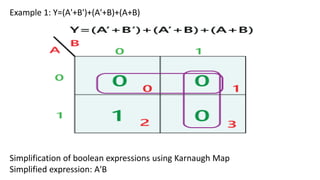
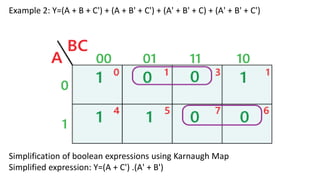
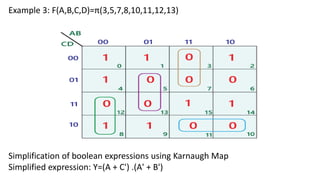
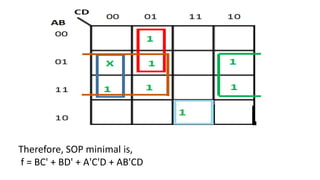
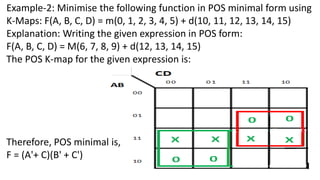
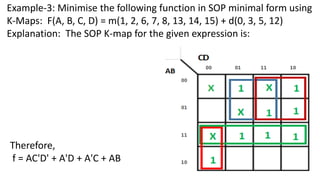
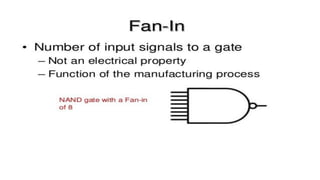
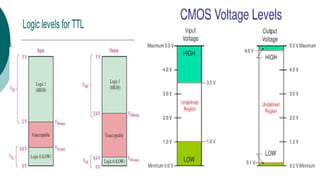
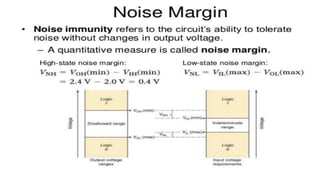
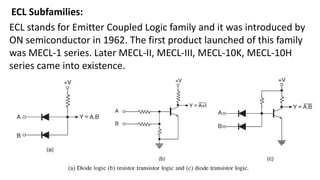
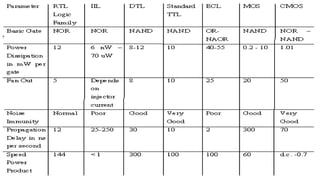
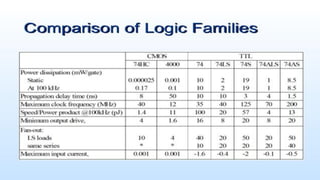
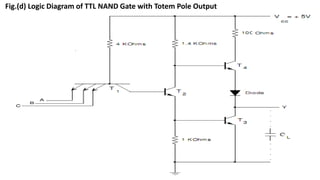
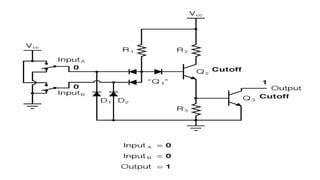
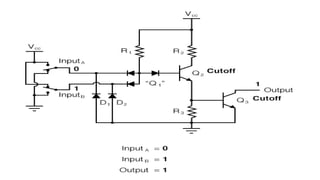
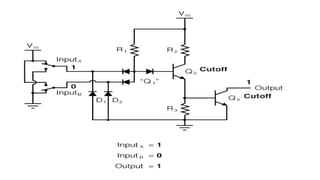
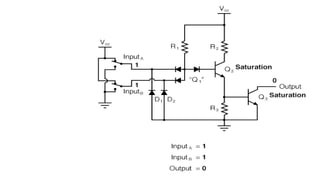
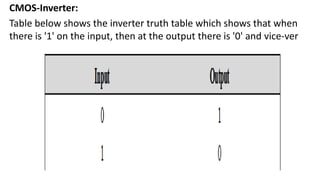
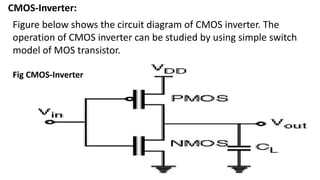
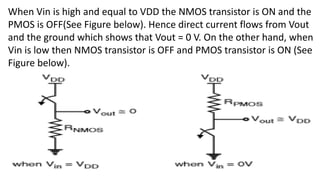
Boolean algebra deals with logical operations on binary variables that have two possible values, typically represented as 1 and 0. George Boole first introduced Boolean algebra in 1854. Boolean algebra uses logic gates like AND, OR, and NOT as basic building blocks. Positive logic represents 1 as high and 0 as low, while negative logic uses the opposite. Boolean algebra laws and Karnaugh maps are used to simplify logical expressions. Don't care conditions allow for groupings in K-maps that further reduce expressions.