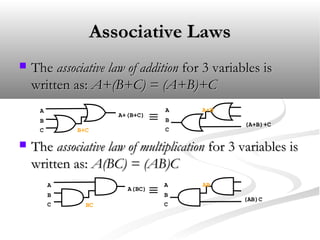
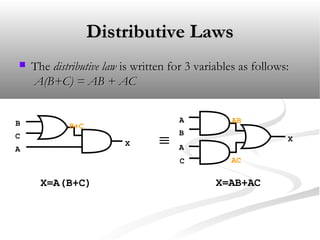
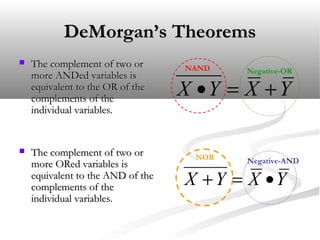
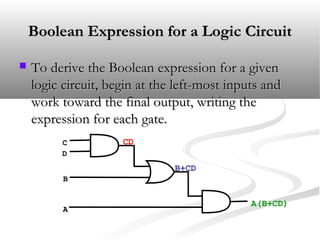
George Boole first introduced Boolean algebra in 1854 as a way to systematically analyze logic circuits. Boolean algebra represents logical variables and operations using algebra, allowing the behavior of circuits to be expressed with equations. A Boolean expression can be derived for any logic circuit and a truth table constructed to show the output for all combinations of inputs.

1. Boolean AlgebraBoolean Algebra

2. IntroductionIntroduction
 1854:1854: Logical algebraLogical algebra was published bywas published by GeorgeGeorge
BooleBoole  known today as “Boolean Algebra”known today as “Boolean Algebra”
 It’s a convenient way and systematic way ofIt’s a convenient way and systematic way of
expressing and analyzing the operation of logicexpressing and analyzing the operation of logic
circuits.circuits.
 1938:1938: Claude ShannonClaude Shannon was the first to applywas the first to apply
Boole’s work to the analysis and design of logicBoole’s work to the analysis and design of logic
circuits.circuits.

3. Boolean Operations & ExpressionsBoolean Operations & Expressions
 VariableVariable – a symbol used to represent a logical– a symbol used to represent a logical
quantity.quantity.
 ComplementComplement – the inverse of a variable and is– the inverse of a variable and is
indicated by a bar over the variable.indicated by a bar over the variable.
 LiteralLiteral – a variable or the complement of a– a variable or the complement of a
variable.variable.

4. Boolean AdditionBoolean Addition
 Boolean addition is equivalent to the OR operationBoolean addition is equivalent to the OR operation
 AA sum termsum term is produced by an OR operation with nois produced by an OR operation with no
AND ops involved.AND ops involved.
 i.e.i.e.
 AA sum termsum term is equal to 1 when one or more of the literals in theis equal to 1 when one or more of the literals in the
term are 1.term are 1.
 AA sum termsum term is equal to 0 only if each of the literals is 0.is equal to 0 only if each of the literals is 0.
0+0 = 0 0+1 = 1 1+0 = 1 1+1 = 1
DCBACBABABA +++++++ ,,,

5. Boolean MultiplicationBoolean Multiplication
 Boolean multiplication is equivalent to the ANDBoolean multiplication is equivalent to the AND
operationoperation
 AA product termproduct term is produced by an AND operation with nois produced by an AND operation with no
OR ops involved.OR ops involved.
 i.e.i.e.
 AA product termproduct term is equal to 1 only if each of the literals in theis equal to 1 only if each of the literals in the
term is 1.term is 1.
 AA product termproduct term is equal to 0 when one or more of the literals areis equal to 0 when one or more of the literals are
0.0.
0·0 = 0
DBCACABBAAB ,,,
0·1 = 0 1·0 = 0 1·1 = 1

6. Laws & Rules of Boolean AlgebraLaws & Rules of Boolean Algebra
 The basic laws of Boolean algebra:The basic laws of Boolean algebra:
 TheThe commutativecommutative lawslaws ((กฏการสลับที่กฏการสลับที่))
 TheThe associativeassociative lawslaws ((กฏการจัดกลุ่มกฏการจัดกลุ่ม))
 TheThe distributivedistributive lawslaws ((กฏการกระจายกฏการกระจาย))

7. Commutative LawsCommutative Laws
 TheThe commutative law of additioncommutative law of addition for two variablesfor two variables
is written as:is written as: A+B = B+AA+B = B+A
 TheThe commutative law of multiplicationcommutative law of multiplication for twofor two
variables is written as:variables is written as: AB = BAAB = BA
A
B
A+B
B
A
B+A≡
A
B
AB
B
A
B+A≡

8. Associative LawsAssociative Laws
 TheThe associative law of additionassociative law of addition for 3 variables isfor 3 variables is
written as:written as: A+(B+C) = (A+B)+CA+(B+C) = (A+B)+C
 TheThe associative law of multiplicationassociative law of multiplication for 3 variables isfor 3 variables is
written as:written as: A(BC) = (AB)CA(BC) = (AB)C
A
B
A+(B+C)
C
A
B
(A+B)+C
C
A
B
A(BC)
C
A
B
(AB)C
C
≡
≡
B+C
A+B
BC
AB

9. Distributive LawsDistributive Laws
 TheThe distributive lawdistributive law is written for 3 variables as follows:is written for 3 variables as follows:
A(B+C) = AB + ACA(B+C) = AB + AC
B
C
A
B+C
≡
A
B
C
A
X
X
AB
AC
X=A(B+C) X=AB+AC

10. Rules of Boolean AlgebraRules of Boolean Algebra
1.6
.5
1.4
00.3
11.2
0.1
=+
=+
=•
=•
=+
=+
AA
AAA
AA
A
A
AA
BCACABA
BABAA
AABA
AA
AA
AAA
+=++
+=+
=+
=
=•
=•
))(.(12
.11
.10
.9
0.8
.7
___________________________________________________________
A, B, and C can represent a single variable or a combination of variables.

11. DeMorgan’s TheoremsDeMorgan’s Theorems
 DeMorgan’s theorems provide mathematicalDeMorgan’s theorems provide mathematical
verification of:verification of:
 the equivalency of the NAND and negative-ORthe equivalency of the NAND and negative-OR
gatesgates
 the equivalency of the NOR and negative-ANDthe equivalency of the NOR and negative-AND
gates.gates.

12. DeMorgan’s TheoremsDeMorgan’s Theorems
 The complement of two orThe complement of two or
more ANDed variables ismore ANDed variables is
equivalent to the OR of theequivalent to the OR of the
complements of thecomplements of the
individual variables.individual variables.
 The complement of two orThe complement of two or
more ORed variables ismore ORed variables is
equivalent to the AND of theequivalent to the AND of the
complements of thecomplements of the
individual variables.individual variables.
YXYX +=•
YXYX •=+
NAND Negative-OR
Negative-ANDNOR

13. DeMorgan’s Theorems (Exercises)DeMorgan’s Theorems (Exercises)
 Apply DeMorgan’s theorems to the expressions:Apply DeMorgan’s theorems to the expressions:
ZYXW
ZYX
ZYX
ZYX
•••
++
++
••

14. DeMorgan’s Theorems (Exercises)DeMorgan’s Theorems (Exercises)
 Apply DeMorgan’s theorems to the expressions:Apply DeMorgan’s theorems to the expressions:
)(
)(
FEDCBA
EFDCBA
DEFABC
DCBA
+++
++
+
++

15. Boolean Analysis of Logic CircuitsBoolean Analysis of Logic Circuits
 Boolean algebra provides a concise way toBoolean algebra provides a concise way to
express the operation of a logic circuit formedexpress the operation of a logic circuit formed
by a combination of logic gatesby a combination of logic gates
 so that the output can be determined for variousso that the output can be determined for various
combinations of input values.combinations of input values.

16. Boolean Expression for a Logic CircuitBoolean Expression for a Logic Circuit
 To derive the Boolean expression for a givenTo derive the Boolean expression for a given
logic circuit, begin at the left-most inputs andlogic circuit, begin at the left-most inputs and
work toward the final output, writing thework toward the final output, writing the
expression for each gate.expression for each gate.
C
D
B
A
CD
B+CD
A(B+CD)

17. Constructing a Truth Table for aConstructing a Truth Table for a
Logic CircuitLogic Circuit
 Once the Boolean expression for a given logicOnce the Boolean expression for a given logic
circuit has been determined, a truth table thatcircuit has been determined, a truth table that
shows the output for all possible values of theshows the output for all possible values of the
input variables can be developed.input variables can be developed.
 Let’s take the previous circuit as the example:Let’s take the previous circuit as the example:
A(B+CD)A(B+CD)
 There are four variables, hence 16 (2There are four variables, hence 16 (244
) combinations) combinations
of values are possible.of values are possible.

18. Constructing a Truth Table for aConstructing a Truth Table for a
Logic CircuitLogic Circuit
 Evaluating the expressionEvaluating the expression
 To evaluate the expressionTo evaluate the expression A(B+CD)A(B+CD), first find the, first find the
values of the variables that make the expressionvalues of the variables that make the expression
equal to 1 (using the rules for Boolean add & mult).equal to 1 (using the rules for Boolean add & mult).
 In this case, the expression equals 1 only if A=1 andIn this case, the expression equals 1 only if A=1 and
B+CD=1 becauseB+CD=1 because
A(B+CD) = 1A(B+CD) = 1··1 = 11 = 1

19. Constructing a Truth Table for aConstructing a Truth Table for a
Logic CircuitLogic Circuit
 Evaluating the expression (cont’)Evaluating the expression (cont’)
 Now, determine whenNow, determine when B+CDB+CD term equals 1.term equals 1.
 The termThe term B+CD=1B+CD=1 if eitherif either B=1B=1 oror CD=1CD=1 or if bothor if both
BB andand CDCD equal 1 becauseequal 1 because
B+CD = 1+0 = 1B+CD = 1+0 = 1
B+CD = 0+1 = 1B+CD = 0+1 = 1
B+CD = 1+1 = 1B+CD = 1+1 = 1
 The termThe term CD=1CD=1 only ifonly if C=1C=1 andand D=1D=1

20. Constructing a Truth Table for aConstructing a Truth Table for a
Logic CircuitLogic Circuit
 Evaluating the expression (cont’)Evaluating the expression (cont’)
 Summary:Summary:
 A(B+CD)=1A(B+CD)=1
 WhenWhen A=1A=1 andand B=1B=1 regardless of the values ofregardless of the values of CC andand DD
 When A=1When A=1 andand C=1C=1 andand D=1D=1 regardless of the value ofregardless of the value of BB
 The expressionThe expression A(B+CD)=0A(B+CD)=0 for all other valuefor all other value
combinations of the variables.combinations of the variables.

21. Constructing a Truth Table for aConstructing a Truth Table for a
Logic CircuitLogic Circuit
 Putting the results inPutting the results in
truth table formattruth table format
INPUTSINPUTS OUTPUTOUTPUT
AA BB CC DD A(B+CD)A(B+CD)
00 00 00 00
00 00 00 11
00 00 11 00
00 00 11 11
00 11 00 00
00 11 00 11
00 11 11 00
00 11 11 11
11 00 00 00
11 00 00 11
11 00 11 00
11 00 11 11
11 11 00 00
11 11 00 11
11 11 11 00
11 11 11 11
INPUTSINPUTS OUTPUTOUTPUT
AA BB CC DD A(B+CD)A(B+CD)
00 00 00 00
00 00 00 11
00 00 11 00
00 00 11 11
00 11 00 00
00 11 00 11
00 11 11 00
00 11 11 11
11 00 00 00
11 00 00 11
11 00 11 00
11 00 11 11
11 11 00 00 11
11 11 00 11 11
11 11 11 00 11
11 11 11 11 11
When A=1 and
B=1 regardless
of the values of
C and D
When A=1 and C=1
and D=1 regardless of
the value of B
A(B+CD)=1
INPUTSINPUTS OUTPUTOUTPUT
AA BB CC DD A(B+CD)A(B+CD)
00 00 00 00
00 00 00 11
00 00 11 00
00 00 11 11
00 11 00 00
00 11 00 11
00 11 11 00
00 11 11 11
11 00 00 00
11 00 00 11
11 00 11 00
11 00 11 11 11
11 11 00 00 11
11 11 00 11 11
11 11 11 00 11
11 11 11 11 11
INPUTSINPUTS OUTPUTOUTPUT
AA BB CC DD A(B+CD)A(B+CD)
00 00 00 00 00
00 00 00 11 00
00 00 11 00 00
00 00 11 11 00
00 11 00 00 00
00 11 00 11 00
00 11 11 00 00
00 11 11 11 00
11 00 00 00 00
11 00 00 11 00
11 00 11 00 00
11 00 11 11 11
11 11 00 00 11
11 11 00 11 11
11 11 11 00 11
11 11 11 11 11