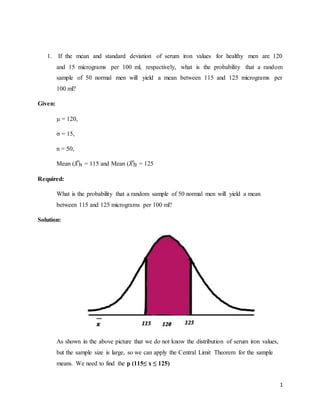
1. The probability that a random sample of 50 normal men will yield a mean serum iron level between 115 and 125 micrograms per 100 ml is approximately 98.18%. 2. The mean of the sampling distribution for the mean serum cholesterol level of US females based on samples of size 50 is 204 mg/dl. The standard error is 6.22 mg/dl. 3. The probability that a resident consumes at most 3 types of food is 0.7675 or 76.75%.

1. COLLEGE OF HEALTH SCIENCE
SCHOOL OF MEDICINE
DEPARTMENT OF MEDICAL PHYSIOLOGY
BIOSTATISTICS ASSIGNMENT
PREPARED BY: HABTEMARIAM MULUGETA
ABATE
ID NO: GSR/2895/14
ADDIS ABABA, ETHIOPIA

2. 1
NOVEMBER, 2021

3. 1
1. If the mean and standard deviation of serum iron values for healthy men are 120
and 15 micrograms per 100 ml, respectively, what is the probability that a random
sample of 50 normal men will yield a mean between 115 and 125 micrograms per
100 ml?
Given:
µ = 120,
σ = 15,
n = 50,
Mean (𝑋̅)1 = 115 and Mean (𝑋̅)2 = 125
Required:
What is the probability that a random sample of 50 normal men will yield a mean
between 115 and 125 micrograms per 100 ml?
Solution:
As shown in the above picture that we do not know the distribution of serum iron values,
but the sample size is large, so we can apply the Central Limit Theorem for the sample
means. We need to find the p (115≤ x ≤ 125)

4. 2
Therefore, p (115 ≤ 𝑋̅ ≤ 125) = p[
(115 − 120)
15
√50
⁄
] ≤ [
(X
̅− µ)
σ
√𝑛
⁄
] ≤ [
(125 − 120)
15
√50
⁄
]
p (115 ≤ 𝑋̅ ≤ 125) = p[
(115 − 120)
15
√50
⁄
] ≤ 𝑍 ≤ [
(125 − 120)
15
√50
⁄
]
p (115 ≤ 𝑋̅ ≤ 125) = p (−2.357 ≤ 𝑍 ≤ 2.357 )
Since the Z table shows at two decimal places, I approximated the values to two decimal
places. p (115 ≤ 𝑋̅ ≤ 125) = p (-2.36 ≤ Z ≤ 2.36)
p (115 ≤ 𝑋̅ ≤ 125) = p (𝑍 ≤ 2.36 )− 𝑝 (𝑍 ≤ − 2.36)
p (115 ≤ 𝑋̅ ≤ 125) = 0.9909 - 0.0091
p (115 ≤ 𝑋̅ ≤ 125) = 0.9818
Thus, approximately 98.18 % of normal sample will yield a mean between 115 and 125
micrograms per 100 ml.
2. The National Health and Nutrition Examination Survey of 1988–1994 (NHANES III, A-
1) estimated the mean serum cholesterol level for U.S. females aged 20–74 years to be 204
mg/dl. The estimate of the standard deviation was approximately 44. Using these estimates
as the mean x and standard deviation s for the U.S. population, consider the sampling
distribution of the sample mean based on samples of size 50 drawn from women in this age
group. What is the mean of the sampling distribution? The standard error?
Given:
Mean (𝑋̅) = 204
σ = 44,
n = 50,
Required:
What is the mean of the sampling distribution?
The standard error?

5. 3
Solution:
The mean of the sampling distribution 𝑿̅
Mean(𝑋̅) = µ = 204
The standard error of 𝑿̅
S.E =
σ
√n
=
44
√50
= 6.22
Use the following table for question #3 - #6
Variety of food in number (x) Probability of consuming that variety of food (P(X=x))
1 0.4231
2 0.3321
3 0.0123
4 0.1431
5 0.0231
6 0.0663
3. What is the probability that a resident consumes at most three types of food?
Probability that a resident consumes at most three types of food = (P ≤ 3)
(P ≤ 3) = (P = 1) + (P = 2) + (P = 3)
(P ≤ 3) = 0.4231 + 0.3321 + 0.0123
(P ≤ 3) = 0.7675
Therefore, the probability that a resident consumes at most three types of food = (P ≤ 3)
is 0.7675 (76.75 %)
4. What is the probability that a resident consumes at least four types of food?
Probability that a resident consumes at least four types of food = (P ≥ 4)
(P ≥ 4) = (P = 4) + (P = 5) + (P = 6)
(P ≥ 4) = 0.1431 + 0.0231 + 0.0663
(P ≥ 4) = 0.2325

6. 4
Therefore, the probability that a resident consumes at least four types of food = (P ≥ 4) is
0.2325 (23.25 %)
5. What is expected value/Population mean?
The expected value (EV) is calculated by multiplying each of the possible outcomes by the
likelihood each outcome will occur and then summing all of those values.
EV = ∑ P(Xi) × Xi
EV = (1 × 0.4231) + (2 × 0.3321) + (3 × 0.0123) + (4 × 0.1431) + (5 × 0.0231) + (6 × 0.0663)
EV = 0.4231 + 0.6642 + 0.0369 + 0.5724 + 0.1155 + 0.3978
EV = 2.2099
Therefore, the expected value (population mean) is 2.2099
6. What is the variance of the population around the mean?
σ = √𝑉𝑎𝑟 (𝑋)
σ2 = [(1 - 2.2099)2 0.4231] + [(2 - 2.2099)2 0.3321] + [(3 - 2.2099)2 0.0123] + [(4 - 2.2099)2
0.1431] + [(5 - 2.2099)2 0.0231] + [(6 - 2.2099)2 0.0663]
σ2 = [(-1.2099)2 0.4231] + [(- 0.2099)2 0.3321] + [(0.7901)2 0.0123] + [(1.7901)2 0.1431] +
[(2.7901)2 0.0231] + [(3.7901)2 0.0663]
σ2 = [0.61935832] + [0.0146316651] + [0.0076783735] + [0.4585579412] + [0.1798256] +
[0.9523900861]
σ2 = 2.2324419859 σ = √𝑉𝑎𝑟 (𝑋) σ = √2.2324419859
Therefore, the variance of the population around the mean is 2.23

7. 5
7. In Lami Kura sub-city (Addis Ababa), cases of COVID-19 was reported with a rate of
6.5/day. What is the probability that 2 cases of COVID-19 will be reported in a given day?
(e = 2.71)
Given:
λ = the mean number of occurrences in periods of some interval = 6.5/day
X = the event of the random variable X = 2
e = 2.71
Required:
What is the probability that 2 cases of COVID-19 will be reported in a given day?
Solution:
P(X=x) =
𝑒−λλ 𝑥
𝑋!
P(X=x) =
(𝑒−6.5)6.5 2
2!
= 0.0635203059/2 = 0.031760153
8. Suppose a borderline hypertensive is defined as a person whose DBP is between 80- and
95-mm Hg inclusive, and the subjects are 35-44-year-old males whose BP is normally
distributed with mean 75 and variance 121. What is the probability that a randomly selected
person will be a borderline hypertensive?
Given:
Mean = 75
Variance = 121
DBP is between 80- and 95-mm Hg inclusive.
Required:
What is the probability that a randomly selected person will be a borderline hypertensive?

8. 6
Solution:
Let X be DBP, X ~ N (75, 121)
σ = √𝑉𝑎𝑟𝑖𝑎𝑛𝑐𝑒 = √121 = 11
P (80 < 𝑋̅ < 95) = P [
(80 − 75)
11
] < [
(X
̅− µ)
σ
] < [
(95 − 75)
11
]
P (80 < 𝑋̅ < 95) = P [
(80 − 75)
11
] < 𝑍 < [
(95 − 75)
11
]
P (80 < 𝑋̅ < 95) = P (0.45454545454545454545454545454545 < 𝑍 <
1.8181818181818181818181818181818)
Since the Z table shows at two decimal places, I approximated the values to two decimal
places. P (80 < 𝑋̅ < 95) = P (0.46 < 𝑍 < 1.82)
P (80 < 𝑋̅ < 95) = P (0.46 < 𝑍 < 1.82)
P (80 < 𝑋̅ < 95) = P (Z < 1.82) – P (Z < 0.46)
P (80 < 𝑋̅ < 95) = 0.9656 – 0.6772
P (80 < 𝑋̅ < 95) = 0.2884
Thus, approximately 28.84 % of this population will be borderline hypertensive.
9. The mean reading speed of a random sample of 81 adults is 325 words per minute. If the
standard deviation for all adults is 45 words per minute; Find a 90% C.I.
Given:
n = 81
𝑋̅ = 325
σ = 45
90% C.I. = 1.645
Required: Find a 90% C.I.

9. 7
Solution:
𝑋̅ ± Za⁄2 (
σ
√𝑛
)
325±1.645(
45
√81
)= 325±1.645(
45
9
)
325±1.645(5)= 325± 8.225 = (325 - 8.225, 325 + 8.225)
Therefore, the 90% C.I. is (316.775, 333.225)
10.An anthropologist who wanted to study the heights of adult men and women
took a random sample of 128 adult men and 100 adult women which is
normally distributed. Adult men population mean height and SDwere 170cms
and 8cms respectively. Whereas for women 164cms and 6cms respectively.
Find a 95% C.I for the difference of mean height of adult men and women.
Given:
n1 = 128 and n2 = 100
𝑋̅1 = 170 and 𝑋̅2 = 164
σ1 = 8 and σ2 = 6
Required: Find a 95% C.Ifor the difference of mean height ofadult men and women.
Solution:
𝑋̅1 - 𝑋̅2 ± Za⁄2 (√
σ12
𝑛1
+
σ22
𝑛2
) = 170 - 164 ± 1.96(√
82
128
+
62
100
)

10. 8
170 - 164 ± 1.96(√
82
128
+
62
100
)= 6 ± 1.96(√
64
128
+
36
100
) = 6 ± 1.96(√0.5 + 0.36)
170- 164 ± 1.96(√
82
128
+
62
100
)= 6 ± 1.96(√0.86) = 6 ± 1.96(0.927) = 6 ± 1.81692
6 ± 1.81692 = (6 – 1.81692, 6 + 1.81692) = (4.18308, 7.81692)
Therefore, the 95% C.I for the difference of mean height of adult men and women
is (4.18308, 7.81692).