1. Reed-Solomon Code adalah teknik pengkodean error-correcting yang populer untuk komunikasi satelit, magnetic storage, dan HDTV. 2. Teknik ini bekerja dengan menambahkan redundansi data ke dalam pesan asli untuk kemudian didekode dan dikoreksi kesalahan dalam proses decoding. 3. Algoritma encoding dan decoding melibatkan aritmatika di bidang Galois untuk mendeteksi dan memperbaiki kesalahan.

1. Adi Suheryadi
adi.suheryadi@gmail.com

2. [1] Encoding –Decoding Reed Solomon Code
Komunikasi data digital[1]

3. •Oleh Irving Reed dan Gustave Solomon pada tahun 1960[2]
•Merupakan teknik pengkodean yang dijadikan standar dalam banyak hal seperti komunikasi satelit dan mobile, magnetic record, high defination televition[3]
•Non binary code (diolah dalam word) sehingga lebih cepat dalam proses encoding dan decoding dibandingkan dengan algoritma error correction lainnya yang menggunakan binary code
•Bekerja dengan menambahkan informasi tambahan (redundansi data) di dalam data asli
•Systematic linear block code dan Nonbinary ciclic code
[2] Reed, I. S. and Solomon, G., “Polynomial Codes Over Certain Finite Fields,” SIAM Journal of Applied Math., vol. 8, 1960, pp. 300-304
[3] Reed-Solomon Code., by Bernard Sklar

4. •Notasi : RS(n,k)
•k : jumlah simbol data
•n : panjang simbol codeword
•2t : panjang simbol parity
•Tiap simbol dikodekan sebanyak m-bit, maka panjang codeword yang dapat dibentuk adalah n = 2m-1
•Bentuk generatornya :
Parity (2t)
Simbol data (k)
n Symbol
k Symbol
2t Symbol

5. •Pembentukan polinomial codeword
U(x)=p(x)+푥푛−푘 m(x)
dimana :
U(x) = codeword yang dibentuk
m(x) = simbol informasi yang dikodekan
p(x) = parity
•Parity didapat dari :
p(x)=푥푛−푘 m(x) mod g(x)
•Kemampuan RS-Code
Deteksi dan koreksi sebanyak t error
2t = n-k  t = (n-k)/2 simbol error

6. •Contoh 1
misal RS (15,11), maka informasi yang didapat :
•n = 15
•k = 11
•t = (n - k) / 2 = (15 - 11)/2
•GF (16), maka m =4
•Pada p = 0 , maka g(x) =
•m = 8 bit
•n = 255, k = 223 simbol
•2t = n-k = 32, t = 16

7. •Aritmatika Galois Field
•Finite Field GF(p)
•Primitive Polynomial
•Extension Field GF(푝푚)

8. •Dalam reed solomon code oprasi aritmatik didakukan dalam Galois Field aritmatic
•Himpunan yang memiliki elemen terbatas contoh GF(24) maka memiliki 16 elemen
•Bilangan prima p  GF(p), p elemen
•GF(p) pm elemen  extension field of GF(p)
GF(pm), m = bilangan bulat positif > 0
•Reed-Solomon Code : GF(2m)
{0,a0,a1,a2,…,a2m+2}

9. •Mendefinisikan GF(2m) yang dinotasikan dengan pilinomial f(x) atau g(x)
•Sifat polinom f(x) tidak dapat direduksi dan difaktorkan ke yang lebih kecil
•Polinom g(x) berderajad m yang tidak bisa direduksi dikatakan primitif jika bilangan positif terkecil n yang membagi habis f(x) terhadap xn+1 adalah n = 2m-1
•1 + x + x4
•1 + x + x2 + x3 + x4
•m= 4, n = 2m-1 = 15  x15+1

12. •m = 3  GF(23) = GF(8)
•f(X) = 1 + X + X3 = 0
•X  a
•f(a) = 0
•1 + a + a3 = 0
•a3 = -1-a  a3 = 1+ a
•a4 = a.a3 = a.(1+a) = a+a2,
•a5 = a.a4 = a.(a+a2) = a2+a3 = 1+a+a2
•a6 = a.a5 = a.(1+a+a2) = a+a2+a3 = 1+a2
•a7 = a.a6 = a.(1+a2) = a+a3 = 1 = a0
•GF(23) = {0,a0,a1,a2,a3,a4,a5,a6}

13. X0
X1
X2
Desimal
0
0
0
0
0
a0
1
0
0
1
a1
0
1
0
2
a2
0
0
1
4
a3
1
1
0
3
a4
0
1
1
6
a5
1
1
1
7
a6
1
0
1
5
a7
1
0
0
1

15. •a+a = a-a = 0, a.a = a

17. •Polinon quotient : q(x), Polinom parity : p(x), Polinom message : M(x), Polinom remainder : r(x), Polinom transmition : T(x)
•Secara sistematik
Geser ke kanan M(x) sebanyak n-k hingga ke sisi paling kanan kodeword, lalu tambahkan p(x) untuk mengisi sisi paling kiri dari codeword
Xn-k.M(X) = q(X).g(X) + p(X)
p(X) = Xn-k.m(X) mod g(X)
•Polinom Codeword
T(X) = p(X) + Xn-k.m(X)

18. 1.Dapatkan fungsi generator g(x)
2.Membentuk polinomoial M(x)
3.Geser polinomial M(x), dengan cara M(x)xn-k
4.Kemudian dapatkan polinomial remainder r(x), dengan cara membagi M(x)xn-k dengan g(x)
5.Pisahkan polinomial quotient q(x)
6.Susun polinomial T(x)
7.Konversi polinomial T(x)

19. •RS(n,k)
•n = 2m-1 dan k = n-2t = 2m-1-2t,
•(n,k) = (2m-1,2m-1-2t)
•g(X) = (X - a)(X – a2) … (X – a2t)
•RS(7,3)  n=7,k=3, n-k=4

20. •Encoding pesan :2 3 4 dengan RS (7,3)
maka didapat :
Jumlah codeword n = 7
Jumlah data k = 3
Jumlah parity = n – k =4
2t = n-k, maka t = (n-k)/2 = 4/2 =2
n = 2m – 1, maka m = 3, sehingga GF (23)
Generator : g(x) = x4 + a3 x3 + a0 x2 + a1 x + a3

21. 1.Generator :
g(x) = x4 + a3 x3 + a0 x2 + a1 x + a3
g(x) = x4 + 3 x3 + x2 + 2 x + 3
2.M(x) = 2 x2 + 3 x + 4
3.M(x) x4 = 2 x6 + 3 x5 + 4 x4
4.r(x) = 7 x3 + 5 x2 + 4 x + 2
5.q(x) = 2 x2 + 5 x + 2
6.T(x) = 2 x6 + 3 x5 + 4 x4 + 7 x3 + 5 x2 + 4 x + 2
7.T(x) = a1 x6 + a3 x5 + a2 x4 + a5 x3 + a6 x2 + a2 x + a1
8.Jika dikonversi ke binar adalah 010110001111101001010

23. Sehingga kode yang dikirimkan adalah penambahan hasil dari Stage Shift Register dan Data itu sendiri, menghasilkan sebagai berukut :

25. Dimana:
a merupakan received code
b merupakan syndrome polinomial
c merupakan error locator polinomial
d merupakan error value
e merupakan error location
f merupakan corecting error

26. •Received pattern
•R(X) = T(X) + E(X)
dimana :
•R(X) : Polinomial data yang diterima
•E(X) : Polinomial Error
•Error pattern

27. T(X) = a0 + a2X + a4X2 + a6X3 + a1X4 + a3X5 + a5X6
R(X) = (100) + (001) X + (011)X2 + (100)X3 + (101)X4 + (110)X5 + (111)X6
Maka dapat dapat dituliskan :
R(X) = a0 + a2 X + a4X2 + a0X3 + a6X4 + a3X5 + a5X6
Codeword Sent
100001011101010110111
Codeword Received
10000101110 0101110111

28. •Parity check pada R(X) untuk memastikan R(X) valid
•Membagi R(X) dengan masing-masing dari code polinomial
•Jika syndrome bernilai 0 maka R(X) valid
•Terbentuk dari n-k simbol
•{ Si }, i = 1..n-k
•Si  substitusi X dengan ai, i = 1…n-k
•Cara lain mencari syndrom

29. R(X) = a0 + a2 X + a4X2 + a0X3 + a6X4 + a3X5 + a5X6
RS(7,3)  n = 7, k = 3
{ Si }, i = 1..n-k = 1..4
•S1 = r(a) = a0 + a3 + a6 + a3 + a10 + a8 + a11 = a3
•S2 = r(a2) = a0 + a4 + a8 + a6 + a14 + a13 + a17 = a5
•S3 = r(a3) = a0 + a5 + a10 + a9 + a18 + a18 + a23 = a6
•S4 = r(a4) = a0 + a6 + a12 + a12 + a22 + a23 + a29 = 0
•ΣSi ≠ 0  codeword mengandung error

30. Horner methode
S3 = r(a3) = 8

31. •Misal terdapat sejumlah v error pada posisi
•Xj1 Xj2,…Xjv
•Maka polinom error :
•Bl = ajl , subtitusikan ai pada R(X) untuk i = 1..2t

32. •Polinom Error Locator L(X) atau (X)
•L(X) = 1 + L1X + L2X2 + … + LvXv
•L(X) = (1+B1X) (1+B2X) … (1+BvX)
•Akar dari L(X) = 1/B1, 1/B2, … 1/Bv
•Kebalikan dari akar L(X) adalah nomor lokasi error dari error pattern e(X), maka menggunakan teknik autoregresif modeling kita dapatkan

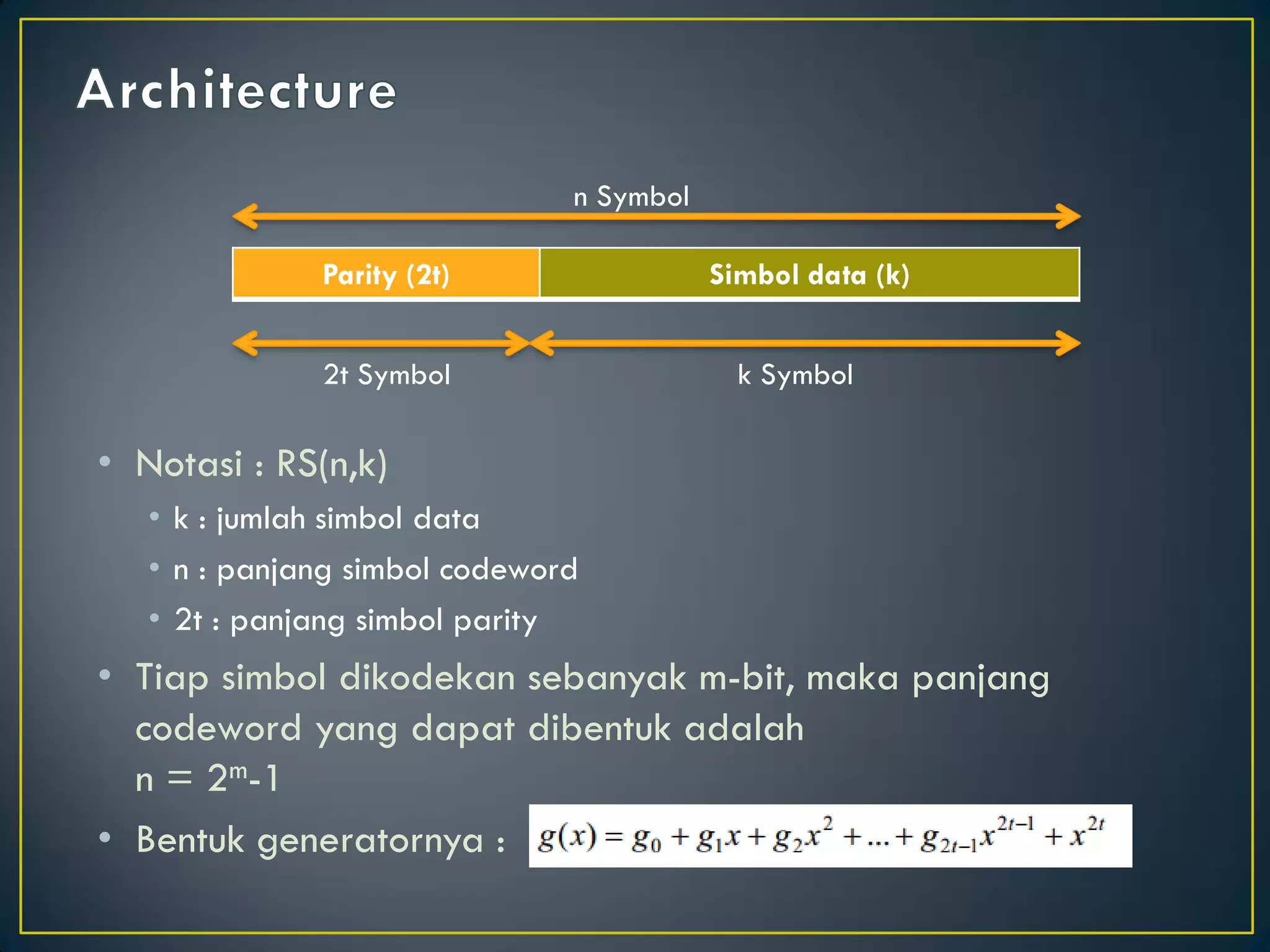
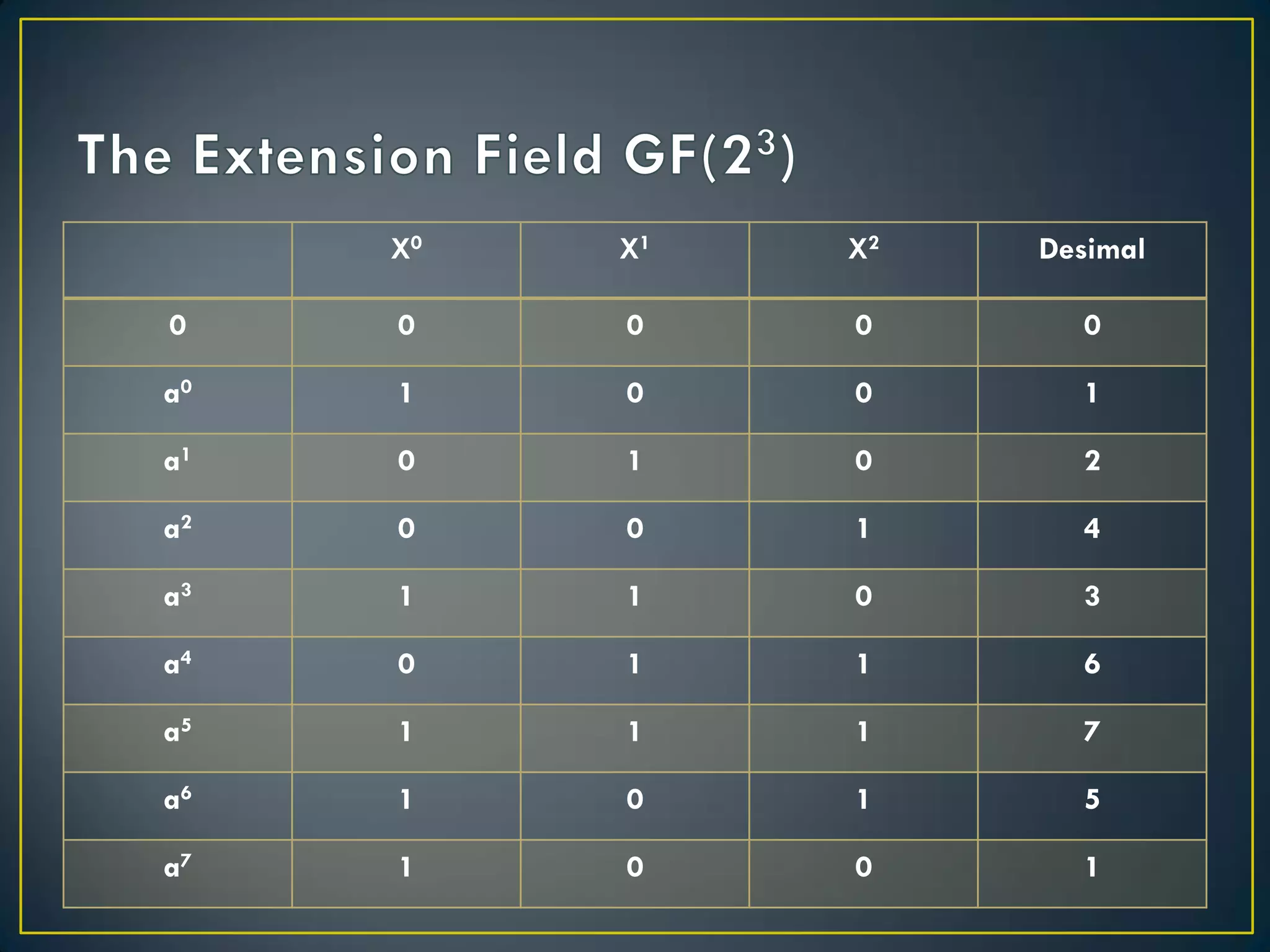
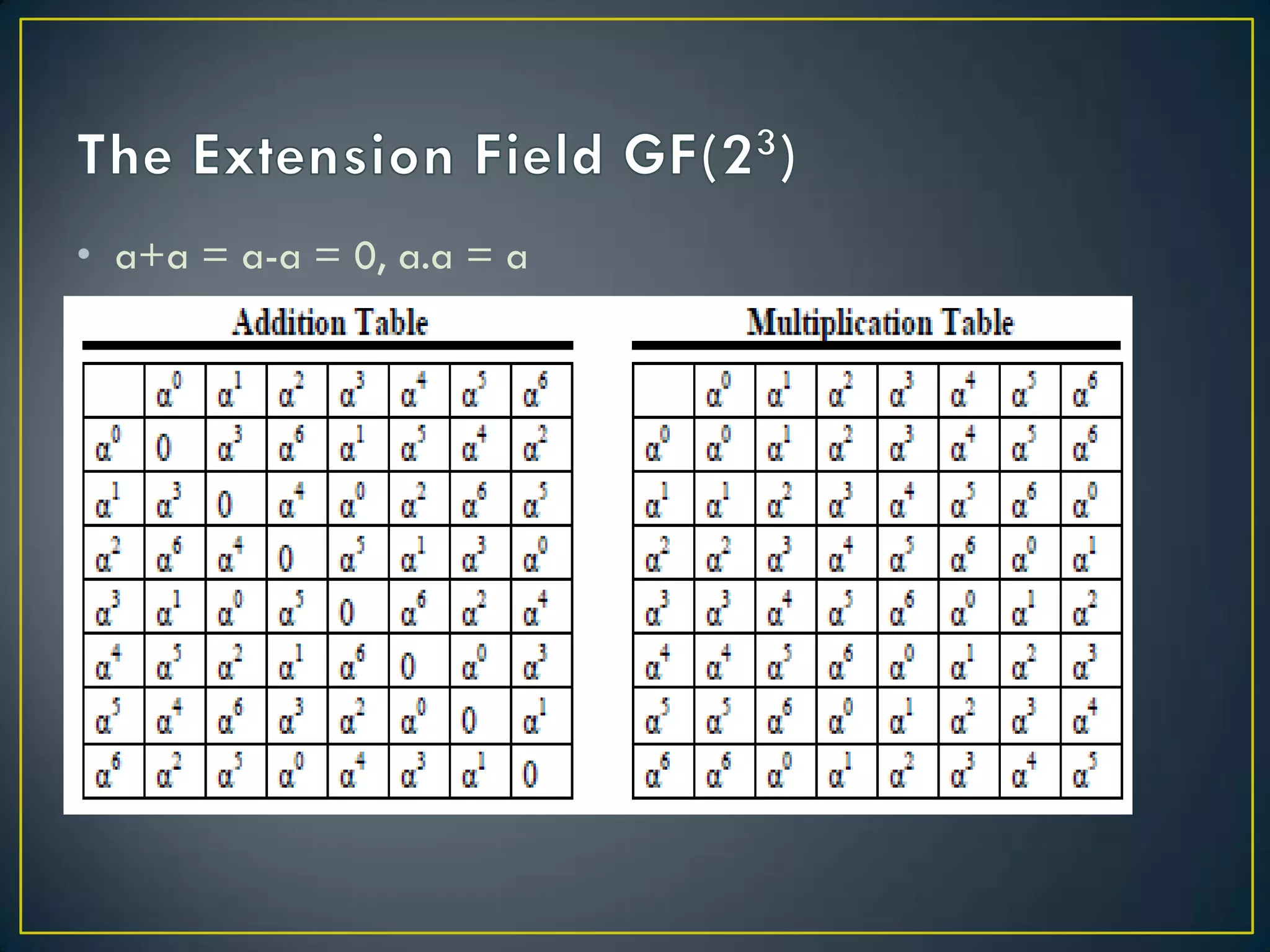
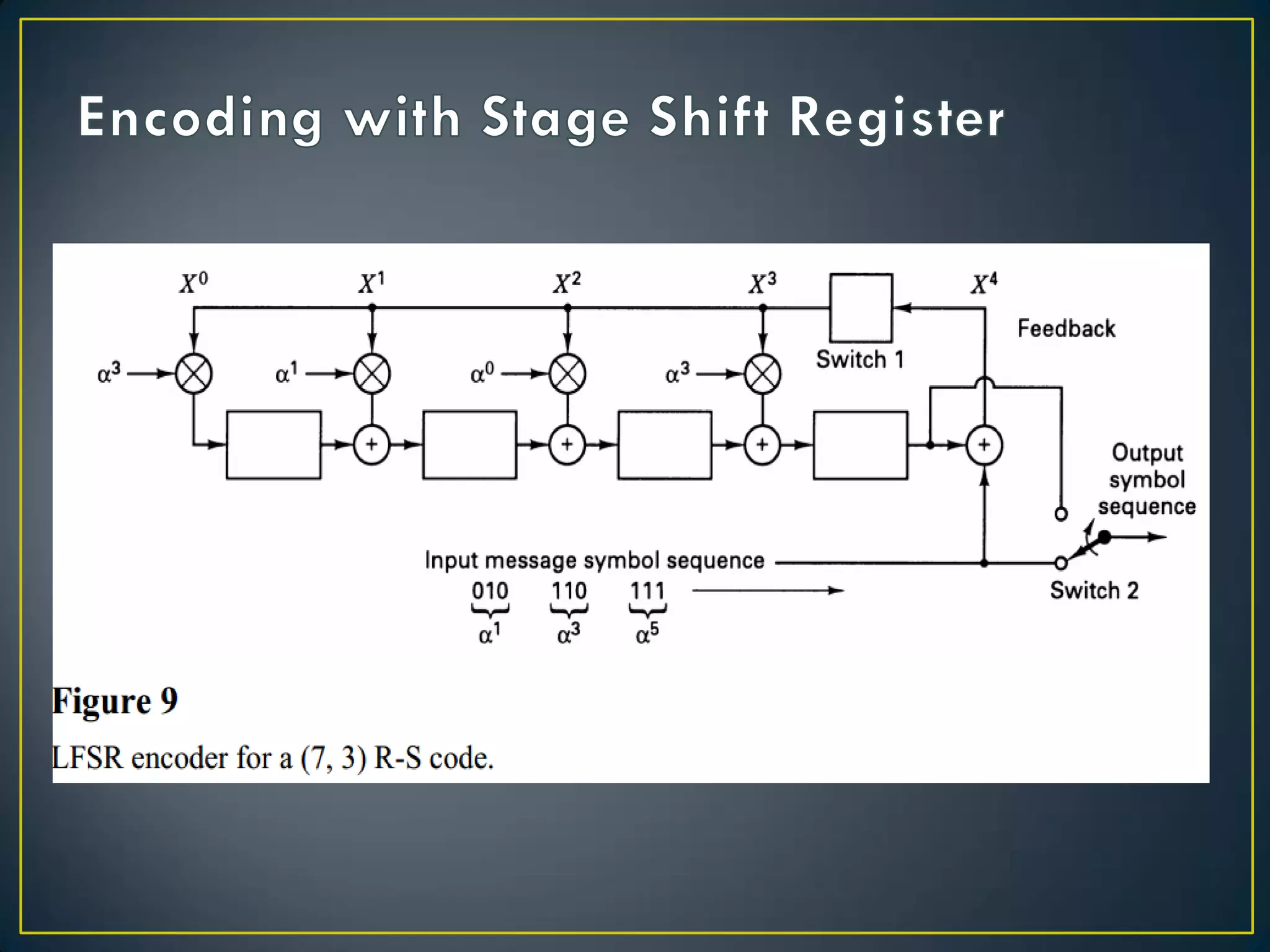
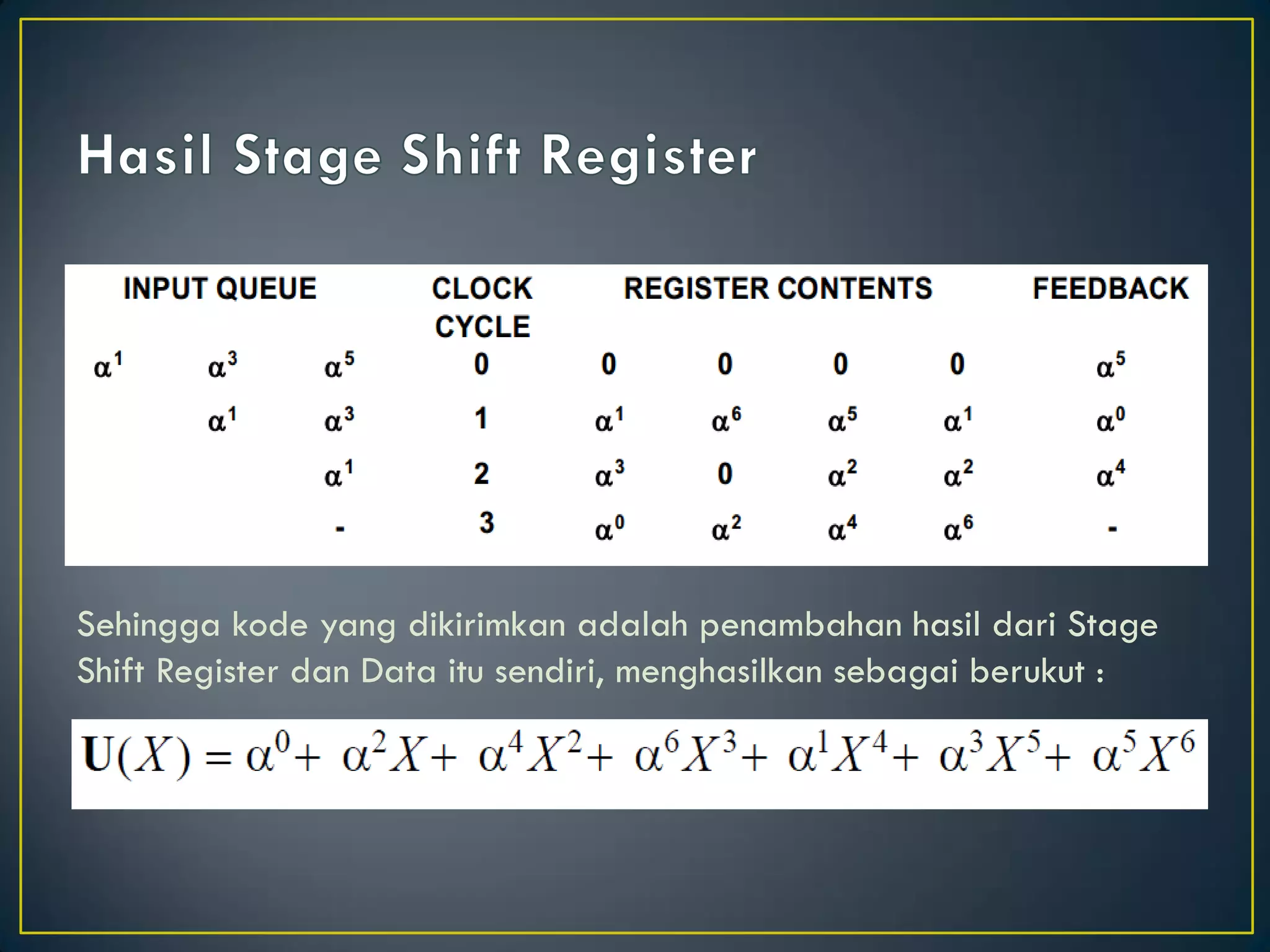
33. •Dari contoh
•Penyelesaian koefisien L1 dan L2
•Inv[A] = cofactor[A]/det[A]

34. •Sehingga kita dapatkan polinom L(X)

35. •Akar dari L(X) adalah posisi error pada r(X)
•cara paling brute force : coba subtitusi masing2 elemen GF pada L(X), jika L(X) bernilai 0, maka elemen tersebut adalah akar dari L(X)  lokasi error

36. •Didapat akar L(X)
•1/B1 = a3  B1 = 1/a3  B1 = a4
•1/B2 = a4  B2 = 1/a4  B2 = a3

37. •Subtitusi akar L(X) ke Syndrome manapun
•Sehingga bisa kita tuliskan matrix persamaan

38. •Hitung e1 dan e2
•Sehingga kita dapat

39. •Hitung
•Kemudian kita dapatkan

40. •Sehingga untuk
•U(X) = (100) + (001) X + (011)X2 + (101)X3 + (010)X4 + (110)X5 + (111)X6
•r(X) = (100) + (001) X + (011)X2 + (100)X3 + (101)X4 + (110)X5 + (111)X6
•ê(X) = (000) + (000) X + (000)X2 + (001)X3 + (111)X4 + (000)X5 + (000)X6
•Kita dapatkan
•Û(X) = (100) + (001) X + (011)X2 + (101)X3 + (010)X4 + (110)X5 + (111)X6

41. Hasil corrected code
Û(X) = (100) + (001) X + (011)X2 + (101)X3 + (010)X4 + (110)X5 + (111)X6
•Karena symbol pesan mengkonstitusikan rightmost k=3 simbol,
•maka pesan yang didekodekan =
•a1 a3 a5 = 010 110 111

42. 1.Encoding – Decoding Reed Solomon Code
2.Reed, I. S. and Solomon, G., “Polynomial Codes Over Certain Finite Fields,” SIAM Journal of Applied Math., vol. 8, 1960, pp. 300-304
3.Bernard Sklar., Reed-Solomon Code
4.Baharuddin dan Rahmat., Analisis Pengguna Pengkodean Reed Solomon Terhadap Kualitas Transmisi Citra
5.Teori Encoding – Decoding Reed Solomon Code
6.León van de Pavert, REED-SOLOMON ENCODING AND DECODING
7.C.K.P. Clark, Reed Solomon Error Correction, BBC- R&D White Paper