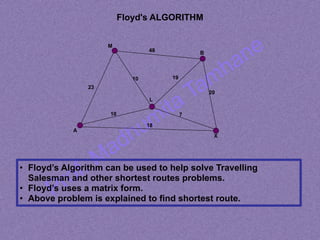
The document explains Floyd's algorithm, which is employed to solve shortest path problems, including the traveling salesman problem. It describes the process of using a distance matrix to find the shortest routes between vertices by iterations, making necessary adjustments to the matrix based on comparisons of distances. The final output is a modified route matrix that provides insights into the optimal paths between nodes.

1. Prof. Madhumita Tamhane
Floyd's ALGORITHM

2. Prof. Madhumita TamhaneM
B
L
A
X
48
20
10 19
18
710
23
• Floyd’s Algorithm can be used to help solve Travelling
Salesman and other shortest routes problems.
• Floyd’s uses a matrix form.
• Above problem is explained to find shortest route.
Floyd's ALGORITHM

3. Prof. Madhumita Tamhane
D( 0 ) R( 0 )
This is the distance matrix.
It initially shows the direct
distance between one vertex
and the others. The infinity sign
denotes no direct route.
This is the route matrix.
It will eventually show the
next vertex that needs to be
taken on route to finding the
shortest route to another vertex.
A M L B X
A 23 10 18
M 23 10 48
L 10 10 19 7
B 48 19 20
X 18 7 20
A M L B X
A 1 2 3 4 5
M 1 2 3 4 5
L 1 2 3 4 5
B 1 2 3 4 5
X 1 2 3 4 5
∞
∞
∞
∞
∞ ∞
∞
∞
∞

4. Prof. Madhumita Tamhane
D( 0 ) R( 0 )
We highlight the first column and row of the Distance matrix and compare
all other items with the sum of the items highlighted in the same row and
column.
If the sum is less than the item then it should be replaced with the sum.
A M L B X
A 23 10 18
M 23 10 48
L 10 10 19 7
B 48 19 20
X 18 7 20
A M L B X
A 1 2 3 4 5
M 1 2 3 4 5
L 1 2 3 4 5
B 1 2 3 4 5
X 1 2 3 4 5
∞ ∞
∞ ∞
∞
∞ ∞
∞ ∞

5. Prof. Madhumita Tamhane
D( 0 ) R( 0 )
23 + 23 = 46, less than so
change.
A M L B X
A 23 10 18
M 23 10 48
L 10 10 19 7
B 48 19 20
X 18 7 20
A M L B X
A 1 2 3 4 5
M 1 2 3 4 5
L 1 2 3 4 5
B 1 2 3 4 5
X 1 2 3 4 5
∞
We highlight the first column and row of the Distance matrix and compare
all other items with the sum of the items highlighted in the same row and
column.
If the sum is less than the item then it should be replaced with the sum.
∞ ∞
∞ ∞
∞
∞ ∞
∞ ∞

6. Prof. Madhumita Tamhane
D( 0 ) R( 0 )
23 + 23 = 46, less than so
change.
A M L B X
A 23 10 18
M 23 46 10 48
L 10 10 19 7
B 48 19 20
X 18 7 20
∞
A M L B X
A 1 2 3 4 5
M 1 2 3 4 5
L 1 2 3 4 5
B 1 2 3 4 5
X 1 2 3 4 5
We highlight the first column and row of the Distance matrix and compare
all other items with the sum of the items highlighted in the same row and
column.
If the sum is less than the item then it should be replaced with the sum.
∞ ∞
∞
∞
∞ ∞
∞ ∞

7. Prof. Madhumita Tamhane
D( 0 ) R( 0 )
18 + 18 = 36, so replace this item.
!
Hence finally we have changed all desired cells in first iteration where sum is less
than the cell data.
!
Now whichever cell is changed, we put 1 (for node A) in corresponding cells in
matrix R(0). Finally at the end of first iteration…..
A M L B X
A 23 10 18
M 23 46 10 48 41
L 10 10 20 19 7
B 48 19 20
X 18 41 7 20 36
A M L B X
A 1 2 3 4 5
M 1 2 3 4 5
L 1 2 3 4 5
B 1 2 3 4 5
X 1 2 3 4 5
We highlight the first column and row of the Distance matrix and compare
all other items with the sum of the items highlighted in the same row and
column.
If the sum is less than the item then it should be replaced with the sum.
∞ ∞
∞ ∞

8. Prof. Madhumita Tamhane
R( 0 )
A M L B X
A 23 10 18
M 23 46 10 48 41
L 10 10 20 19 7
B 48 19 20
X 18 41 7 20 36
D( 0 )
A M L B X
A 1 2 3 4 5
M 1 1 3 4 1
L 1 2 1 4 5
B 1 2 3 4 5
X 1 1 3 4 1
∞ ∞
∞ ∞

9. Prof. Madhumita Tamhane
We have now completed one iteration. We rename the new matrices:
Subsequent iterations are now shown completed:
R( 1 )D( 1 )
A M L B X
A 23 10 18
M 23 46 10 48 41
L 10 10 20 19 7
B 48 19 20
X 18 41 7 20 36
A M L B X
A 1 2 3 4 5
M 1 1 3 4 1
L 1 2 1 4 5
B 1 2 3 4 5
X 1 1 3 4 1
∞ ∞
∞ ∞

10. Prof. Madhumita Tamhane
In second iteration, second row and column are highlighted. Similarly other cells are compared with
Sum of corresponding row and column and changed as before.
Corresponding cell at R(0) will have 2 (for node M). Result is …
R( 1 )D( 1 )
A M L B X
A 23 10 18
M 23 46 10 48 41
L 10 10 20 19 7
B 48 19 20
X 18 41 7 20 36
A M L B X
A 1 2 3 4 5
M 1 1 3 4 1
L 1 2 1 4 5
B 1 2 3 4 5
X 1 1 3 4 1
∞
∞ ∞
∞

11. Prof. Madhumita Tamhane
D( 1 ) R( 1 )
The items have been altered accordingly:
Subsequent iterations are now shown completed:
A M L B X
A 46 23 10 71 18
M 23 46 10 48 41
L 10 10 20 19 7
B 71 48 19 96 20
X 18 41 7 20 36
A M L B X
A 1 2 3 4 5
M 1 1 3 4 1
L 1 2 1 4 5
B 1 2 3 4 5
X 1 1 3 4 1

12. Prof. Madhumita Tamhane
D( 2 ) R( 2 )
We can now rename the matrices:
Similarly do 3rd, 4th and 5th iteration by highlighting 3rd, 4th and 5th
row and column respectively. Change cells of R(0) to 3, 4 or 5
accordingly. Final matrix is …
A M L B X
A 46 23 10 71 18
M 23 46 10 48 41
L 10 10 20 19 7
B 71 48 19 96 20
X 18 41 7 20 36
A M L B X
A 2 2 3 2 5
M 1 1 3 4 1
L 1 2 1 4 5
B 2 2 3 2 5
X 1 1 3 4 1

13. Prof. Madhumita Tamhane
D( 2 ) R( 2 )
Next iteration:
A M L B X
A 46 23 10 71 18
M 23 46 10 48 41
L 10 10 20 19 7
B 71 48 19 96 20
X 18 41 7 20 36
A M L B X
A 2 2 3 2 5
M 1 1 3 4 1
L 1 2 1 4 5
B 2 2 3 2 5
X 1 1 3 4 1

14. Prof. Madhumita Tamhane
D( 2 ) R( 2 )
Next iteration, the items are altered appropriately :
A M L B X
A 20 20 10 29 17
M 20 20 10 29 17
L 10 10 20 19 7
B 29 29 19 38 20
X 17 17 7 20 14
A M L B X
A 3 3 3 3 3
M 3 3 3 3 3
L 1 2 1 4 5
B 3 3 3 3 5
X 3 3 3 4 3

15. Prof. Madhumita Tamhane
D( 3 ) R( 3 )
The matrices are renamed :
A M L B X
A 20 20 10 29 17
M 20 20 10 29 17
L 10 10 20 19 7
B 29 29 19 38 20
X 17 17 7 20 14
A M L B X
A 3 3 3 3 3
M 3 3 3 3 3
L 1 2 1 4 5
B 3 3 3 3 5
X 3 3 3 4 3

16. Prof. Madhumita Tamhane
The next iteration :
D( 3 ) R( 3 )
A M L B X
A 20 20 10 29 17
M 20 20 10 29 17
L 10 10 20 19 7
B 29 29 19 38 20
X 17 17 7 20 14
A M L B X
A 3 3 3 3 3
M 3 3 3 3 3
L 1 2 1 4 5
B 3 3 3 3 5
X 3 3 3 4 3

17. Prof. Madhumita Tamhane
In this iteration, you do not need to change any of the items, so we go
onto the next iteration :
D( 3 ) R( 3 )
A M L B X
A 20 20 10 29 17
M 20 20 10 29 17
L 10 10 20 19 7
B 29 29 19 38 20
X 17 17 7 20 14
A M L B X
A 3 3 3 3 3
M 3 3 3 3 3
L 1 2 1 4 5
B 3 3 3 3 5
X 3 3 3 4 3

18. Prof. Madhumita Tamhane
A M L B X
A 20 20 10 29 17
M 20 20 10 29 17
L 10 10 20 19 7
B 29 29 19 38 20
X 17 17 7 20 14
A M L B X
A 3 3 3 3 3
M 3 3 3 3 3
L 1 2 1 4 5
B 3 3 3 3 5
X 3 3 3 4 3
D( 4 ) R( 4 )

19. Prof. Madhumita Tamhane
There is only one item that we need to change in this
case:
D( 4 ) R( 4 )
A M L B X
A 20 20 10 29 17
M 20 20 10 29 17
L 10 10 14 19 7
B 29 29 19 38 20
X 17 17 7 20 14
A M L B X
A 3 3 3 3 3
M 3 3 3 3 3
L 1 2 1 4 5
B 3 3 3 3 5
X 3 3 3 4 3

20. Prof. Madhumita Tamhane
These are the final matrices, remember that you can
use them to redraw the original network. You can then
use this to help us solve travelling salesman problems:
D( 5 ) R( 5 )
A M L B X
A 20 20 10 29 17
M 20 20 10 29 17
L 10 10 14 19 7
B 29 29 19 38 20
X 17 17 7 20 14
A M L B X
A 3 3 3 3 3
M 3 3 3 3 3
L 1 2 5 4 5
B 3 3 3 3 5
X 3 3 3 4 3

21. Prof. Madhumita Tamhane
page 1
M
B
L
A
X
29
20
10 19
17
710
20
29
17
This network now gives you a better idea of the quickest routes.
!The route matrix gives us an idea about the next vertex to visit on route -
1 represents A, 2 - M, etc.

22. Prof. Madhumita Tamhane
1
5
4
3
2
75 35
32
15
40
30
70
Q1.

23. Prof. Madhumita Tamhane
1 2 3 4 5
1 60 30 40 45 77
2 30 30 50 15 47
3 40 50 70 35 67
4 45 15 35 30 32
5 77 47 67 32 64
1 2 3 4 5
1 2 2 3 2 2
2 1 4 4 4 4
3 1 4 4 4 4
4 2 2 3 2 5
5 4 4 4 4 4
D( 5 ) R( 5 )
These are the completed matrices. Are yours correct?

24. Prof. Madhumita Tamhane
1
5
4
3
2
20 15 12
35
50
50
10
Q2.

25. Prof. Madhumita Tamhane
D( 5 ) R( 5 )
These are the completed matrices. Are yours correct?
1 2 3 4 5
1 100 50 50 65 60
2 50 40 20 35 30
3 50 20 20 15 10
4 65 35 15 24 12
5 60 30 10 12 20
1 2 3 4 5
1 2 2 3 3 3
2 1 3 3 4 3
3 1 2 5 4 5
4 3 2 3 5 5
5 3 3 3 4 3