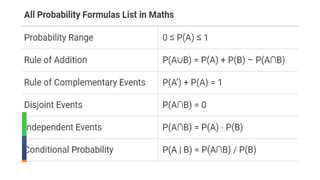
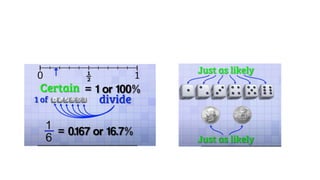
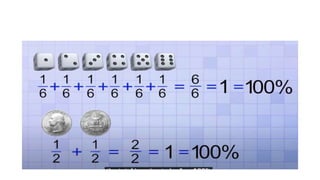
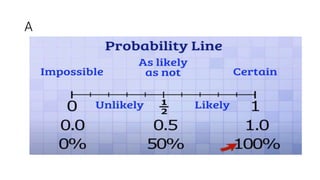
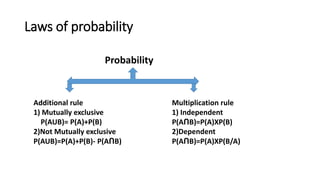
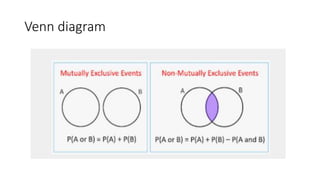
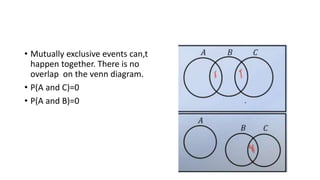
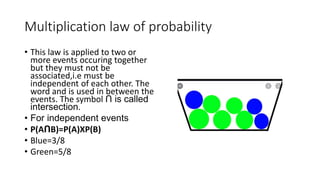
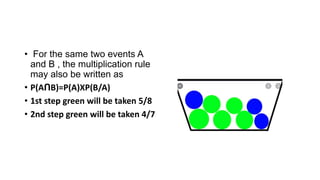
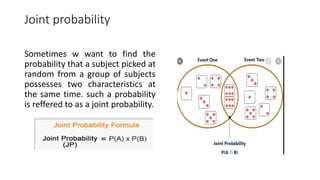
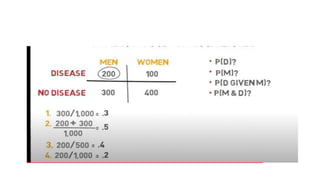
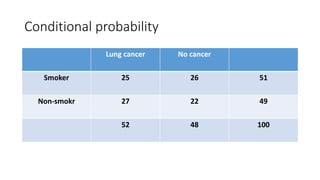
The document discusses key concepts in probability, including: - Probability is a measure of uncertainty or likelihood of outcomes ranging from 0 to 1. - Events can be mutually exclusive, independent, or dependent. Laws of probability like addition and multiplication rules are used based on the relationship between events. - Conditional probability is the probability of one event occurring given that another event has occurred or is known. 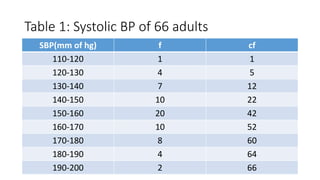- Examples are given to illustrate calculating probabilities of outcomes from experiments or surveys using relative frequency definitions of probability.

1. Dr. Khursheda Akhtar
Assistant Professor
Public Health and Hospital Administration,
NIPSOM
Probability

2. • Usually math always happen in a
certain way.
• like 1+1=2 or 2x3=6 there is no
uncertainty-deterministic
• 4+2=6 (every one)
• sum any two number from 1 to
100 is unpredictable--probalistic

3. • In the early days, probability was
associated with games of chance(gambling)
• Medicine is an inexact science. Probability
provides a measure of inexactness.
• Probability may be defined as the relative
frequency or probable chances of
occurrence with which an event is
expected to occur on an average.
Example:Coin, Dice, Card

5. Random experiment
If an experiment or trail is
repeated under the same
conditions for any number of
times and its possible to count
the total number of outcomes is
called as random experiment.

6. Probability is the study of randomness and uncertainty of any outcome.
The probability of a given event is an expression of likelihood of
occurrence of an event.
A probability is a number which ranges from 0 to 1
0 for an event which cannot occur
I for event which can occur
“Statistics as a method of decision- making under uncertainty, is
founded on probability theory, since probability is at once the language
and the measure of uncertainty and the risks associated with it.”

7. • Likely /unlikely
• relative frequency: the ratio of
the frequency of a particular
event in a statistical experiment
to the total frequency.
• Absolute frequency:?

8. • A surgeon may say that a patient
has 50-50 chance of surving
after operation.
• A physician may say that he is
95% sure that a patient has a
particular disease.
• When p=0, it means there is no
chance of an event happening or
its occurence is impossible.
chance of survival after rabies
are zero or nil
• Probability of survival after sand-
fly fever is 100%

9. • Arithmatically we calculate the
probability(p) or chance of
occurance of a positive event by
the formula:
Probability of occurance of events
‘A’ is denoted ,by P(A)
• P(A)=
𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑓𝑎𝑣𝑜𝑢𝑟𝑎𝑏𝑙𝑒 𝑜𝑢𝑡𝑐𝑜𝑚𝑒
𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑓𝑎𝑣𝑜𝑢𝑟𝑎𝑏𝑙𝑒 𝑜𝑢𝑡𝑐𝑜𝑚𝑒𝑠
P(A) = n(A)/n(S)
Where,
P(A) is the probability of an event “A”
n(A) is the number of favourable outcomes
n(S) is the total number of events in the
sample space

10. • Suppose that in a trail of a new vaccine, 23 of 1000 children
vaccinated showed signs of adverse reaction( such as fever or sign of
irritability) with in 24 hours of vaccination, probability of adverse
reaction is ,
• P(A)=
𝑛(𝐴)
𝑛(𝑆)
=
23
1000
=0.023
=2.3%

11. Complementary event
• Complementary events happen
when there are only two
outcomes, like getting a job, or
not getting a job. In other words,
the complement of an event
happening is the exact opposite:
the probability of it not
happening. It rains or it does not
rain.
• If the probability of an event
happening in a sample is p and
that of not happing is denotes
by the symbol q then p+q=1

12. • If a surgeon transplant kidney in 200 cases
succeeds in 80 cases then probability of
survival after operation is
• 𝑝 =
Number of survivals after the operation
Total number of patients operation
p=
80
200
=0.4
q or probability of not surviving or dying
= 1- 0.4
=0.6

13. Properties of probability
1. Science probability is expressed in terms of relative frequency or
propotion, it can take values between 0 and 1
2. A value 0 means the event cannot occur.
3. A value 1 means the event is certain to occur.
4. A value of 0.5 means the event has equal chance of occurance and
non occurance.
5. The sum of probabilities (relative frequencies) of all events must be
equal to 1 or 100%
6. It is usually expressed with a symbol p

16. A

17. Laws of probability
Probability
Additional rule
1) Mutually exclusive
P(AUB)= P(A)+P(B)
2)Not Mutually exclusive
P(AUB)=P(A)+P(B)- P(AՈB)
Multiplication rule
1) Independent
P(AՈB)=P(A)XP(B)
2)Dependent
P(AՈB)=P(A)XP(B/A)

18. Mutually exclusive events:
• An event is a specific set of outcomes of a random variable.
• Mutually exclusive events can occur only one at a time.
• Exhaustive events cover or contain all possible outcomes.
• The two events or outcomes are said to be mutually exclusive if both
the events cannot occur simultaneously. Tossing of a coin results in
two mutually exclusive outcomes- either a head or a tail can occur at
the same time.
• More trails or experiments conduct the closer your results will get to
the expected posibilities.

19. Venn diagram

20. Table 1: Systolic BP of 66 adults
SBP(mm of hg) f cf
110-120 1 1
120-130 4 5
130-140 7 12
140-150 10 22
150-160 20 42
160-170 10 52
170-180 8 60
180-190 4 64
190-200 2 66

21. 1. P(A) SBP between 130-140=7/66=0.106
2. P(A)SBP<150=(1+4+7+10)/22=0.333
3. Suppose ‘A’ is the event that a person has SBP <150. ‘B’ is an event
that a person with SBP<150 has SBP between (130-140).What is the
probability that a person with SBP<150 has SBP between (130-140).
SBP<150=22(A)
SBP(130-140)=7(B)
P(B/A)= 7/22= 0.32

22. • Mutually exclusive events can,t
happen together. There is no
overlap on the venn diagram.
• P(A and C)=0
• P(A and B)=0

23. Joint probability
Sometimes w want to find the
probability that a subject picked at
random from a group of subjects
possesses two characteristics at
the same time. such a probability
is reffered to as a joint probability.

24. Law od addition
• The probability of any one of mutually exclusive events is the sum of
the probabilities of each event. If A and B are two mutually exclusive
events, then the probability that either A or B will occur is,
• P(AUB) or ((A or B)=P(A)+P(B)
• Probability of occurance of event A + probability of occurance of
event B
• When the two events are mutually exclusive
• Probility of giving Astra Oxford vaccine and Pfizer vaccine to
bangladeshi population.
• The word ‘or’ is there when additional law is applied

25. • If the two events are not mutually exclusive. the additional rule may
be written
• P(AUB)=P(A)+P(B)- P(AՈB)
• Example: For contrilling SBP one group take atenolol, other group
takr ca channel blocker, some take both.

26. Multiplication law of probability
• This law is applied to two or
more events occuring together
but they must not be
associated,i.e must be
independent of each other. The
word and is used in between the
events. The symbol Ո is called
intersection.
• For independent events
• P(AՈB)=P(A)XP(B)
• Blue=3/8
• Green=5/8

27. • For the same two events A
and B , the multiplication rule
may also be written as
• P(AՈB)=P(A)XP(B/A)
• 1st step green will be taken 5/8
• 2nd step green will be taken 4/7

28. Conditional probability
• When probabilities are
calculated with a subset of a
group of the total group as the
denominator, the result is a
conditional probability.
• The conditional probability of A
and B is equal to the probability
of AՈB divided by the
probability of B, provided the
probability of B is not
zero.Symbol Ո is read either
as intersection or and.

29. Types of probability
• Three types of probability
• 1)Theoretical Probability Based on predictable parameters
p(Tossing a five)=1/6
p(Drawing a spade)=1/4
2)Empirical probability-Based on historical and geological records
p(Strong earthquake in the next 10 years)
p(Getting into a car accident)
3)Subjective probability-Based on experience or intuition
p(geting hurt when falling off a bicycle)

30. Independent events
• Independent events have no effect on each other.
• if P(A)XP(B)= P(A and B) then A and B are independent.
• Rain on saturday
• coin toss
• some one study physics/chemistry

36. Conditional probability
Lung cancer No cancer
Smoker 25 26 51
Non-smokr 27 22 49
52 48 100