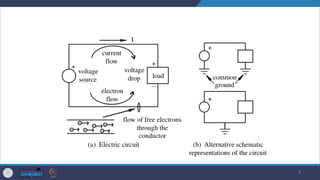
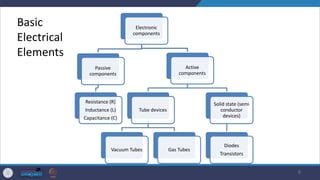
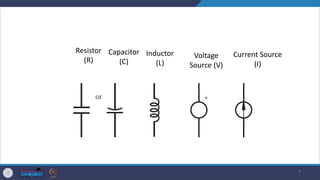
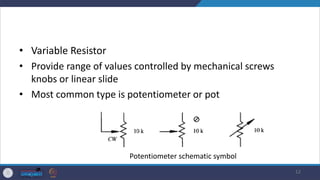
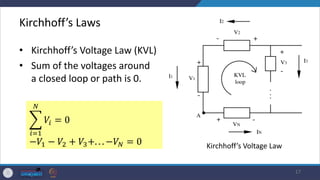
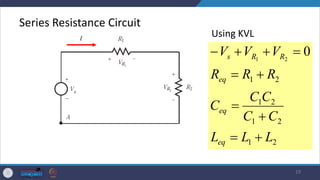
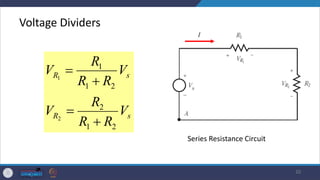
- The document provides an overview of basic concepts in electric circuits and components important for mechatronics, including definitions of voltage, current, resistance, capacitance, inductance, and different circuit types. - It describes common passive components like resistors, capacitors, inductors and discusses their properties and applications. Kirchhoff's laws for circuit analysis are also introduced. - The document concludes by discussing equivalent circuit models like Thevenin and Norton equivalents that are used to simplify complex circuit analyses.

1. MECHATRONICS
ELECTRIC CIRCUITS AND COMPONENTS
PUSHPARAJ MANI PATHAK
MECHANICAL & INDUSTRIAL ENGINEEING, IIT ROORKEE
1

2. Introduction
• Electric circuits and components are important in design of
discrete circuits for signal conditioning and interfacing.
• Electron moves and produce electric current. Useful jobs can
be done by energized electrons.
• Electron moves because we impose an electric field that
imparts energy by doing work on the electrons.
• A measure of electric field potential is voltage.
• Voltage is also referred as electromotive force or emf.
2

3. Electric Circuit Terminology
• Current is time rate of flow of charge
• 𝐼(𝑡) =
𝑑𝑞
𝑑𝑡
(q=charge)
• DC Circuit: Voltage and current in a circuit are constant
(independent of time)
• AC Circuit: Voltage and current vary with time usually
sinusoidally
3

4. 4

5. • Voltage source adds energy to electron.
• Anode: Electrons are attracted.
• Cathode: Electrons are released
• Electron flow from cathode to anode through the circuit. But
standard convention is in opposite direction.
• Load: Network of circuit elements that may store (I,C) or
dissipate electrical energy (R)
• Ground: Indicates a reference point in circuit where the
voltage is assumed to be zero.
5

6. Electronic
components
Passive
components
Resistance (R)
Inductance (L)
Capacitance (C)
Active
components
Tube devices
Vacuum Tubes Gas Tubes
Solid state (semi
conductor
devices)
Diodes
Transistors
6
Basic
Electrical
Elements

7. 7
Resistor
(R)
Capacitor
(C)
Inductor
(L)
Voltage
Source (V)
Current Source
(I)

8. • Passive electrical elements: R, L, C
• Passive elements require no additional power supply, unlike
active devices such as integrated circuits.
• These elements are defined by voltage current relationship.
• Two types of energy sources
• Voltage source (V)
• Current sources (I)
• Ideal source contains no internal resistance, inductance or
capacitance.
8

9. Resistor
• Dissipative element
that converts
electrical energy
into heat.
• Ohms law define V-I
characteristics
(V=IR)
9
R =
𝜌𝐿
𝐴
𝜌 is resistivity of material

10. Resistor Packaging
10

11. Wire Lead Resistor Color Bands
11
Resistor value & tolerance are expressed as
R = ab×10c± tolerance(%)
a band: ten digit
b band: one digit
c band: power

12. • Variable Resistor
• Provide range of values controlled by mechanical screws
knobs or linear slide
• Most common type is potentiometer or pot
12
Potentiometer schematic symbol

13. Capacitor
• Passive element that stores
energy in the form of an electric
field.
• The filed is the result of
separation of charges.
• Dielectric material is an insulator
that increases the capacitance as
a result of permanent or induced
electric dipoles in the material.
13
Parallel Plate Capacitor

14. • Strictly DC current does not flow through the capacitor
• Charges are displaced through circuit.
• Displacement current
• Capacitance is a property of the dielectric material, plate geometry
and plate separation.
• Values of typical capacitors range from 1 pF to 1000 µF
14
𝑉 𝑡 =
1
𝐶
න
0
𝑡
𝐼 𝜏 𝑑𝜏 =
𝑄(𝑡)
𝐶 𝐼 𝑡 = 𝐶
𝑑𝑉
𝑑𝑡

15. Inductor
• A passive element
that stores energy in
the form of a
magnetic field.
• Energy storing
element that stores
energy in the form of
magnetic field.
• Characteristics are
from Faradays law of
induction
15
𝜆 is total magnetic flux through
coil winding due to current. It is
measured in webers(Wb)

=
=
=
=
t
d
V
L
t
I
dt
dI
L
t
V
LI
dt
d
t
V
0
)
(
1
)
(
)
(
)
(





16. • Current through an inductor cannot change instantaneously
because it is integral of voltage.
• Motors have large inductance, so it is difficult to start and
stop motors instantaneously
• Unit of measurement of inductance is Henry
• Typical inductance range from 1µH to 100mH
16

17. Kirchhoff’s Laws
• Kirchhoff’s Voltage Law (KVL)
• Sum of the voltages around
a closed loop or path is 0.
17
෍
𝑖=1
𝑁
𝑉𝑖 = 0
−𝑉1 − 𝑉2 + 𝑉3+. . . −𝑉𝑁 = 0 Kirchhoff’s Voltage Law

18. Kirchhoff’s Current Law (KCL)
• Sum of the currents
flowing into a closed
surface or node is 0.
18

=
=
=
−
+
N
i
i
I
I
I
I
1
3
2
1
0
0
Kirchhoff’s Current Law
𝐼1
𝐼2
𝐼3
Node Surface
𝐼1 𝐼2
𝐼3
𝐼𝑁 …

19. Series Resistance Circuit
19
2
1
2
1
2
1
2
1
0
2
1
L
L
L
C
C
C
C
C
R
R
R
V
V
V
eq
eq
eq
R
R
s
+
=
+
=
+
=
=
+
+
−
Using KVL

20. Voltage Dividers
20
s
R
s
R
V
R
R
R
V
V
R
R
R
V
2
1
2
2
1
1
2
1
+
=
+
=
Series Resistance Circuit

21. Parallel Resistance Circuit
21
2
1
2
1
2
1
2
1
2
1
2
1 0
L
L
L
L
L
C
C
C
R
R
R
R
R
I
I
I
eq
eq
eq
+
=
+
=
+
=
=
−
−
Using KCL

22. Voltage & Current Sources and Meters
• An ideal voltage source: has zero output resistance and
can supply infinite current
• An ideal current source has infinite output resistance and
can supply infinite voltage
• An ideal voltmeter has infinite input resistance and draws
no current.
• An ideal ammeter has zero input resistance and no
voltage drops across it.
22

23. Real Voltage Source with Output Impedance
23
Rout is small

24. Real Current Source with Output Impedance
24
Rout of commercially available
current source is high. So as to
minimise current division effect

25. Real Ammeter with Input Impedance
25
Rin of commercially available ammeter is small
minimizing the voltage drop VR in the circuit.

26. Real Voltmeter with Input Impedance
26
Rin in commercially available voltmeter (an
oscilloscope or multimeter) is very large (1
to 10 MΩ.)

27. 27

28. Thevenin Equivalent Circuit
• To simplify the analysis of complex circuits we wish to replace
voltage sources and resistance networks with an equivalent voltage
source and series resistor.
• Thevenin theorem states that given a pair of terminal in a linear
network , the network may be replaced by an ideal voltage source
Voc in series with a ressitance RTH.
• Voc is equal to the open circuit voltageacross the terminals, andRTH
is the equivalent resistance across the terminals when independent
voltage sources are shorted and independent current sources are
replaced with open circuits..
28

29. 29
2
1
2
1
2
1
2
R
R
R
R
R
V
R
R
R
V
TH
s
OC
+
=
+
=
Thevenin equivalent circuit

30. Norton Equivalent Circuit
• Here the linear network is replaced by an
ideal current source ISC and the Thevenin
resistance RTH in parallel with this source.
• ISC is found by calculating the current that
would flow through the terminals if they
were shorted together having removed the
remaining load circuit.
• It can be shown that the current ISC flowing
through RTH produces the Thevenin voltage.
30
Norton equivalent circuit

31. AC Circuit Analysis
• Sinusoidal Waveform
31

32. • Time shift between the
signal and reference.
• +ve phase angle-leading
waveform.
• -ve phase angle lagging
waveform.
• Frequency of signal
32
t

= 



2
1
=
=
T
f

33. AC Circuit Analysis
33

34. References
• W. Bolton, Mechatronics: Electronic Control Systems in Mechanical
and Electrical Engineering (6th Edition), Pearson, 2015
• D.G. Alciatore and Michael B. Histand, Introduction to
Mechatronics, Tata Mc Graw Hill, 2012.
• Mechatronic System Design; Shetty Dedas, Kolk and Richard
• Mechatronic Handbook: Bishop; CRC press
• R. Merzouki, A. K. Samantaray, P. M. Pathak, B. Ould Bouamama,
Intelligent Mechatronic Systems: Modeling, Control and Diagnosis,
ISBN 978-1-4471-4627-8, 2013, Springer, London
34

35. 35
Thank You