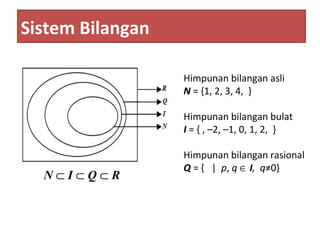
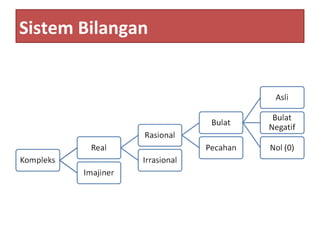
Bab 1 membahas sistem bilangan real, termasuk definisi bilangan bulat, rasional, dan real beserta sifat-sifatnya seperti komutatif, asosiatif, dan distributif. Bab ini juga menjelaskan interval dalam bilangan real seperti selang tertutup, terbuka, dan setengah terbuka. Bab 2 membahas supremum dan infimum sebagai batas atas dan bawah suatu himpunan serta contoh perhitungannya. Bab 3 memfokuskan pada pertid

1. BAB 1
Sistem Bilangan Real

2. Outline Materi

3. 1. Sistem Bilangan

4. Sistem Bilangan
Himpunan bilangan asli
N = {1, 2, 3, 4, }
Himpunan bilangan bulat
I = { , –2, –1, 0, 1, 2, }
Himpunan bilangan rasional
Q = { | p, q ∈ I, q≠0}
N ⊂ I ⊂ Q ⊂ R

5. Sistem Bilangan

6. Sifat-Sifat Bilangan Real
• Komutatif (pertukaran) terhadap penjumlahan dan perkalian
x + y = y + x dan xy = yx
• Asosiatif (pengelompokan) terhadap penjumlahan dan perkalian
(x+y)+z = x+(y+z) dan (xy)z = x(yz)
• Distributif perkalian terhadap penjumlahan
(x+y)z = xz + yz
• Memiliki unsur identitas
– terhadap operasi jumlah yaitu 0 sehingga x + 0 = x ,
– terhadap operasi kali yaitu 1 sehingga x . 1 = x .
• Mempunyai invers
– terhadap penjumlahan yaitu –x, sehingga x + (–x) = 0
– terhadap perkalian yaitu 1/x sehingga x . 1/x = 1.

7. Sifat-Sifat Urutan Bilangan Real
• Trikotomi
Jika x dan y bilangan real, maka berlaku x < y
atau x > y atau x = y.
• Transitif
Jika x < y dan y < z, maka x < z
• Penambahan
x < y ⇔ x + z < y + z
• Perkalian
x < y ⇔ xz < yz, untuk z positif
x < y ⇔ xz > yz, untuk z negatif

8. Sistem Bilangan Real
Himpunan bilangan real dengan semua operasi dan
sifat-sifat yang berlaku di dalamnya dinamakan
sistem bilangan real
Penulisan himpunan dalam bentuk interval / selang:
{x|a ≤ x ≤ b, x∈R} = [a , b] disebut selang tutup
{x|a < x < b, x∈ R } = (a , b) disebut selang buka
{x|a ≤ x < b, x∈ R } = [a , b) disebut selang setengah buka atau selang
setengah tutup
{x|a < x ≤ b, x∈ R } = (a , b] disebut selang setengah buka atau selang
setengah tutup
{x|x ≥ b, x∈ R } = [b , ∞), disebut selang tak terbatas
{x|x < a, x∈ R } = (–∞ , a], disebut selang tak terbatas

9. 2. Supremum Infimum

10. Unsur Maksimum dan Minimum
Definisi
• a ∈ A disebut unsur maksimum dari himpunan A,
apabila untuk semua x ∈ A berlaku x ≤ a.
• b ∈ A disebut unsur minimum dari himpunan A,
apabila untuk semua x ∈ A berlaku x ≥ b.
Contoh
A = (3,7}
Unsur Maksimum A = 7
Unsur Minimum A tidak ada

11. Batas Atas dan Batas Bawah
Definisi
• p ∈ R disebut batas atas dari himpunan A
apabila x ∈ A berlaku x ≤ p
• q ∈ R disebut batas bawah dari himpunan A
apabila x ∈ A berlaku x ≥ q
Contoh
B = (3,7]
batas atas B adalah p ≥ 7
batas bawah B adalah q ≤ 3

12. Supremum dan Infimum
Definisi Supremum
u ∈ R disebut supremum dari himpunan A,
ditulis sup A = u apabila
– u batas atas dari A
– jika t batas atas lain dari A, maka u < t .
Definisi Infimum
v ∈ R disebut infimum dari himpunan A,
ditulis inf A = v apabila
– v batas bawah dari A
– jika s batas bawah lain dari A, maka v > s .

13. Supremum dan Infimum
Contoh
• Untuk A = {1, 2, 3, 4, 5},
maka sup A = 5 dan inf A = 1
• Untuk B = (3,7] ,
maka sup A = 7 dan inf A = 3
Latihan
Tentukan unsur maksimum, unsur minimum, batas atas, batas
bawah, supremum, dan infimum dari himpunan berikut

14. 3. Pertidaksamaan

15. Bentuk-bentuk Pertidaksamaan

16. Catatan
pertidaksamaan tidak boleh dikalikan atau dibagi
oleh suatu variabel karena variabel tersebut bisa
bernilai positif atau negatif.
Pertaksamaan akan berubah tanda apabila variabel
pengali/pembagi bernilai negatif

17. Contoh Soal Pertidaksamaan
Tentukan himpunan penyelesaian dari
1.
2.
3.

18. 4. Nilai Mutlak

19. Definisi Nilai Mutlak
Nilai mutlak x dengan notasi lxl didefinisikan
sebagai:

20. Contoh

21. Akibat Definisi Nilai Mutlak

22. Sifat – Sifat Nilai Mutlak

23. Contoh Soal Nilai Mutlak
Tentukan himpunan penyelesaian dari