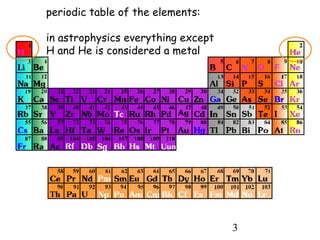
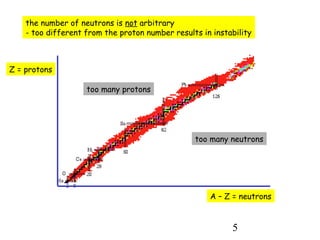
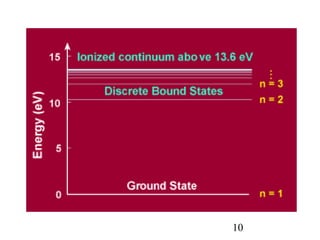
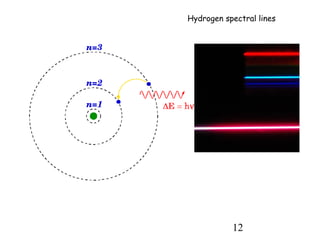
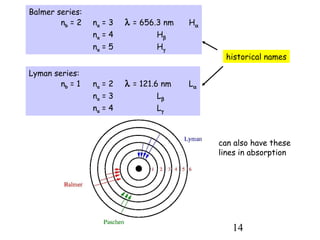
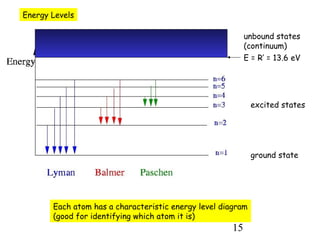
1) Atoms are composed of a small, dense nucleus surrounded by electrons in orbitals. Bohr proposed that electrons can only orbit in discrete energy levels with angular momentum that is quantized. 2) When electrons jump between energy levels, photons are emitted or absorbed with energy equal to the change in energy between the levels. This causes atomic emission and absorption spectra with distinct lines. 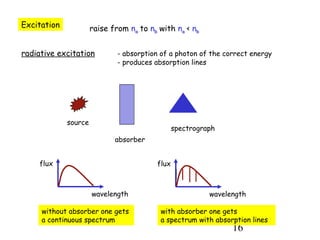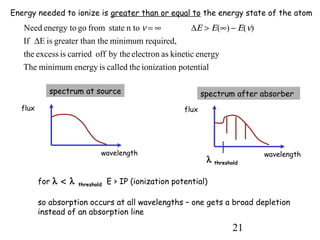3) Excitation of atoms from collisions or photon absorption raises electrons to higher energy levels. Radiative or collisional de-excitation causes emission at characteristic wavelengths corresponding to transitions between levels.

1. 1
Atomic Theory and Spectral Lines -- Chemical Physics
matter is composed of atoms – size ~ 10-8
cm
- density ~ 1023
/cm3
109 different atoms identified - 92 stable (occur naturally)
- 17 transuranic (created artificially)
pattern found by Mendeleev in 1869 (periodic table) led to our currently
accepted model of atoms:
- an atoms is a nucleus (10-14
m) surrounded by a cloud of electrons (10-10
m)
- a nucleus comprises a number of protons with an almost equal number of neutrons
- atomic or chemical properties depend on the electrons (ie on Z, the charge)
(Z = charge on the nucleus = number of protons = number of atomic electrons since atoms are neutral)

2. 2
reminder:
office hours next week only tuesday 2-4

3. 3
periodic table of the elements:
in astrophysics everything except
H and He is considered a metal

4. 4
adding neutrons to a nucleus (or taking them away) does not affect the
nuclear charge (or number of electrons) so chemically the atom is not different
it does affect the nuclear properties (stability etc)
Isotopes
- specify an element by Z
- specify an isotope by A
a complete description requires both
Z is implied by the historical name
eg 14
C A = 14 Z = 6 - carbon with 2 extra neutronss
hydrogen p+e 1
1
H
deuterium p+n+e 1
2
H (in heavy water)
tritium p+n+n+e 1
3
H
these are all isotopes of hydrogen but are not separate elements
they have the same chemical properties but different nuclear properties
(therefore things like nuclear burning in stars are different).

5. 5
the number of neutrons is not arbitrary
- too different from the proton number results in instability
A – Z = neutrons
Z = protons
too many protons
too many neutrons

6. 6
Bohr-Rutherford Model of the Atom
Rutherford (McGill!) discovered the nucleus in experiments where
he scattered alpha particles (helium nuclei – small,dense, + charge)
off thin foils of material and saw that most went right through,
some showed large deflections, and some bounced right back.
he hypothesized that each atom comprised a dense nucleus
orbited by electrons like planets around the sun - mostly space
- the electrostatic (Coulomb) force between the
electrons and the nucleus was the ‘gravity’
major problem with this idea:
- electrons which go in circles are accelerating
- accelerated charges radiate energy
- therefore electrons will lose energy and spiral
into the nucleus – all matter collapses in an instant
- also doesn’t explain discrete lines in spectra
p
e
eg hydrogen

7. 7
Bohr’s hypothesis: classical physics does not apply: quantum theory
electrons only orbit in particular orbits with L (angular momentum)
equal to
where n is an integer and h is Planck’s constant
in this case, with centripetal force equaling the Coulomb force
we have:
but so
solving for r we get:
is a constant for a given atom
is the principal quantum number
the radius of the orbit increases as the
square of the principal quantum number
hn∂nh/ =2
22
/)(/ reZermv =
22
/ mvZer =
mvrnL == h 22
)/()( rnmv h=
22
)//( rnmZer h=
)/(/)( 22222
mZenmZenr hh ==
mZe22
/h
n
π

8. 8
another route to Bohr’s quantum condition: wave/particle duality
wavelength of an orbiting electron (non-relativistic)
p=momentum
circumference must be an integer number
of wavelengths (think standing wave)
the only orbits which can exist have
using the equality of centripetal and Coulomb forces
we get
mvpph /2/2/ hh ππλ ===
λπ nr =2
mvnr /22 hππ =
mvnr /h=
222
// rZermv =
222
)/()/()( rnrZemmv h==
mZenr 222
/h=

9. 9
energy of an electron at radius r
rZemvE /2/ 22
−=
kinetic potential
use )/(/ 22222
mZenmvZer h==
rZerZerZeE 2//2/ 222
−=−= (negative – electrons are bound)
2222
2/)( hnmZeE −=
1/1 2
=−∝ ννΕ has the tightest binding (E is large and negative)
all orbits are bound0→∞→ Εν
0>Ε continuum of unbound states

10. 10

11. 11
Bohr part II:
(a) radiation in the form of a single discreet quantum (photon) is emitted
or absorbed as the electron jumps from one orbit to another
(b) the energy of the radiated photon equals the energy difference between orbits
photons are emitted when the electron goes from a higher energy orbit (na)
to a lower energy orbit (nb) (na > nb)
E(na) = E(nb) + hν
photons are absorbed to cause electrons to go from a lower energy orbit to
a higher energy orbit (nb > na)
E(nb) + hν = E(na)
frequency of emitted (or absorbed) photon:
νab = (E(na) - E(nb) )/h
na is not necessarily nb +/- 1
n = 1 is called the ground state – lower energy states are not possible

12. 12
Hydrogen spectral lines

13. 13
eg Hydrogen Z=1
222
42
1
'
12
)(
n
R
nh
me
nE −=





−=
π
energy of the nth
level
R’ = 2.18 x 10-18
Joules = 13.6 eV (Rydberg energy)
this is often expressed in terms of wavelengths ν = c /λ k = 1/λ = wave number






−=





−=== 2222
1111'1
abab
ab
ab
ab
nn
R
nnhc
R
c
k
υ
λ
R = 10.97 µm-1
(Rydberg constant)
na and nb are two levels in the atom na > nb
for every nb there is an infinite series of nas
na = nb+1, nb+2, nb+3. . .
the series are named after the people who discovered them
Lyman nb = 1 (ultraviolet)
Balmer nb = 2 (found first since it is visible)
Paschen nb = 3
Brackett nb = 4
Pfund nb = 1
remember: E=hν
2222
2/)( hnmZeE −=

14. 14
Balmer series:
nb = 2 na = 3 λ = 656.3 nm Hα
na = 4 Hβ
na = 5 Hγ
Lyman series:
nb = 1 na = 2 λ = 121.6 nm Lα
na = 3 Lβ
na = 4 Lγ
historical names
can also have these
lines in absorption

15. 15
Energy Levels
ground state
excited states
E = R’ = 13.6 eV
unbound states
(continuum)
Each atom has a characteristic energy level diagram
(good for identifying which atom it is)

16. 16
Excitation raise from na to nb with na < nb
radiative excitation - absorption of a photon of the correct energy
- produces absorption lines
source
absorber
spectrograph
flux
wavelength
flux
wavelength
without absorber one gets
a continuous spectrum
with absorber one gets
a spectrum with absorption lines

17. 17
excited states are unstable (10-8
seconds lifetime, typically)
so why don’t the atoms in the absorber de-excite
with no loss of photons and hence no absorption lines?
two reasons:
geometry – decays photons go in all directions so loss of intensity
combinatorics – several de-excitation paths usually available
initial flux
re-emitted flux
λ3
λ2
λ
1
absorb λ1
emit λ2 + λ3

18. 18
collisional excitation - no photons are absorbed; inelastic collisions of the atom
with other atoms or electrons (Coulomb interaction)
- atom gains some of the projectile’s kinetic energy and
has its energy level raised
e
e
vi
vf
γ
hν = 1/2m (vi
2
- vf
2
)
the atom eventually de-excites
through photon emission
we see ‘emission lines’

19. 19
de-excitation
radiative – emission of photon(s) 10-8
seconds typically
collisional – super-elastic collision: excited atom is hit by a particle
or atom which then gains energy from the the collision
forbidden transitions – special form of radiative de-excitation – long
lifetimes since they violate quantum mechanics rules to first
order – have to proceed in a more complicated way which takes
more time. Observation of these implies low temperature and
low density of the region. Otherwise collisions would de-excite
the atoms much sooner.
generally only seen in astrophysics!

20. 20






−=





−=== 2222
1111'1
abab
ab
ab
ab
nn
R
nnhc
R
c
k
υ
λ
Ionization
bound electrons can be liberated from the atom if enough energy
is supplied (by a photon or collision)
E > ∆E (binding energy)
X is an atom
X + energy  X+
+ e-
ion electron
Nomenclature used: hydrogen neutral H or HI
ionized H+
or H II
oxygen neutral O
ionized O+
or O II
twice ionized O++
or O III
++ etc is cumbersome after 3 or 4 electrons have been removed (atoms can be
E
na = ∞

21. 21
Energy needed to ionize is greater than or equal to the energy state of the atom
potentialionizationthecalledisenergyminimumThe
energykineticaselectronby theoffcarriedisexcessthe
required,minimuman thegreater thisEIf
)()(n tostatefromgoenergy toNeed
∆
−∞>∆∞= νΕΕΕν
flux
wavelength
flux
wavelength
spectrum at source spectrum after absorber
λ threshold
for λ < λ threshold E > IP (ionization potential)
so absorption occurs at all wavelengths – one gets a broad depletion
instead of an absorption line

22. 22
Emission continua exist by inverse analogy; if there is a plasma
(ions plus electrons) some recombination can occur if the electron
emits a photon of E = KE + IP
KE = electron’s kinetic energy
IP = ionization potential of the level into which
the electron will fall (not necessarily the ground state)