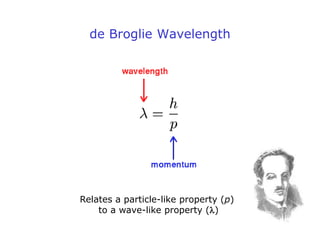
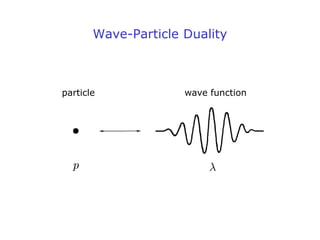
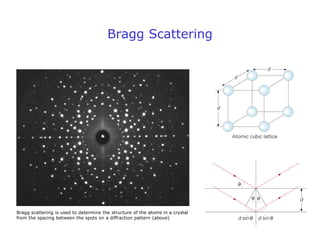
1. Louis de Broglie hypothesized that all matter exhibits both particle-like and wave-like properties, with the wavelength of the matter wave related to the particle's momentum by the de Broglie equation. 2. Experiments demonstrating the wave-like behavior of electrons and other particles validated de Broglie's hypothesis. Electron diffraction and interference patterns exhibited wave-like characteristics. 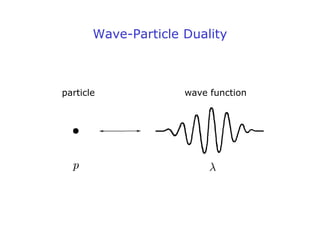3. The wave function describes a particle's quantum mechanical state and contains all observable properties of the particle. It represents the matter wave associated with the particle.

2. Nature of a wave


3. Nature of a particle
 A particle is specified by mass m, velocity v,
momentum p, and energy E
 A particle occupies a definite position in space.
In order for that it must be small

4. Light
 Interference and Diffraction experiments showed the
wave nature of light
 Blackbody radiation and Photoelectric effect can be
explained only by considering light as a stream of
particles

5. So is light a
wave or a particle
?

6. How are they related?
E = hf
 E– energy of the photon
 f– frequency of the wave
 h– plank's constant
p=h/λ
 p – momentum of the particle
  - wavelength of the photon

7. 7
DE BROGLIE HYPOTHESIS
LOUIS DE BROGLIE
“ If radiation which is basically a wave can exhibit
particle nature under certain circumstances, and since
nature likes symmetry, then entities which exhibit
particle nature ordinarily, should also exhibit wave
nature under suitable circumstances”
In the Year 1924 Louis de Broglie
made the bold suggestion
The reasoning used might be paraphrased
as follows
1. Nature loves symmetry
2. Therefore the two great entities,
matter and energy, must be mutually
symmetrical
3. If energy (radiant) is undulatory
and/or corpuscular, matter must be
corpuscular and/or undulatory

8. The de Broglie Hypothesis
 If light can act like a wave sometimes and like a particle
at other times, then all matter, usually thought of as
particles, should exhibit wave-like behaviour
 The relation between the momentum and the
wavelength of a photon can be applied to material
particles also
Prince Louis de Broglie
(1892-1987)

9. de Broglie Wavelength
Relates a particle-like property (p)
to a wave-like property ()
h
mv
 

10. 10
nm
Volts
V
for
thus
nm
V
V
get
we
e
and
m
h
for
ng
substituti
meV
h
mE
h
Then
V
difference
Potential
a
by
d
accelerate
E
Energy
Kinetic
with
electron
an
for
mv
h
p
h
wavelength
Broglie
de
1226
.
0
100
226
.
1
100
226
.
1
10
602
.
1
10
11
.
9
2
10
625
.
6
,
,
2
2
'
'
'
'
particle
the
of
velocity
the
is
v
particle
the
of
mass
the
is
m
Constant
s
Planck'
is
h
19
31
34






















DE BROGLIE WAVELENGTH
The Wave associated with the matter particle is called Matter Wave.
The Wavelength associated is called de Broglie Wavelength.

11. E hf

The frequency
 De Broglie postulated that all particles satisfy
Einstein’s relation
ƒ
E
h

In other words,

12. Example: de Broglie wavelength of an electron
Mass = 9.11 x 10-31 kg
Speed = 106 m / sec
m
10
28
7
m/sec)
kg)(10
10
(9.11
sec
Joules
10
63
6 10
6
31
34








 .
.

This wavelength is in the region of X-rays

13. Example: de Broglie wavelength of a ball
 Mass = 1 kg
Speed = 1 m / sec
m
10
63
6
m/sec)
kg)(1
(1
sec
Joules
10
63
6 34
34






 .
.


14. Theoretical implication – The Bohr
postulate
 Consider standing waves produced in a stretched
string tied at two ends
 Condition for these standing waves is that the length
of the string should be integral multiple of /2

15. Bragg Scattering
Bragg scattering is used to determine the structure of the atoms in a crystal
from the spacing between the spots on a diffraction pattern (above)

16. The Diffraction
X-rays electrons
The diffraction patterns are similar because
electrons have similar wavelengths to X-rays

17. Wave-like Behaviour of Matter
 Evidence:
– electron diffraction
– electron interference (double-slit experiment)
 Also possible with more massive particles,
such as neutrons and a-particles
 Applications:
– Bragg scattering
– Electron microscopes
– Electron- and proton-beam lithography

18. particle wave function
Wave-Particle Duality

19. Wave Function
 Completely describes all the properties of a
given particle
 Called y  y (x,t); is a complex function of
position x and time t

20. particle wave function
Wave-Particle Duality

21. 21
PHASE VELOCITY
Phase velocity: The velocity with which a wave travels is called Phase
velocity or wave velocity. It is denoted by vp. It is given by
v
c
vp
2

Where c = velocity of light and v = is velocity of the particle.
The above equation gives the relationship between the phase velocity and
particle velocity.
It is clear from the above equation that, Phase velocity is not only greater
than the velocity of the particle but also greater than the velocity of light, which
can never happen. Therefore phase velocity has no physical meaning in case of
matter waves. Thus a concept of group velocity was introduced.

22. 22
GROUP VELOCITY
Since phase velocity has no meaning, the concept of group velocity was
introduced as follows.
“ Matter wave is regarded as the resultant of the superposition of large number
of component waves all traveling with different velocities. The resultant is in the
form of a packet called wave packet or wave group. The velocity with which this
wave group travels is called group velocity.” The group velocity is represented by vg.
V
g
Particle
Vp