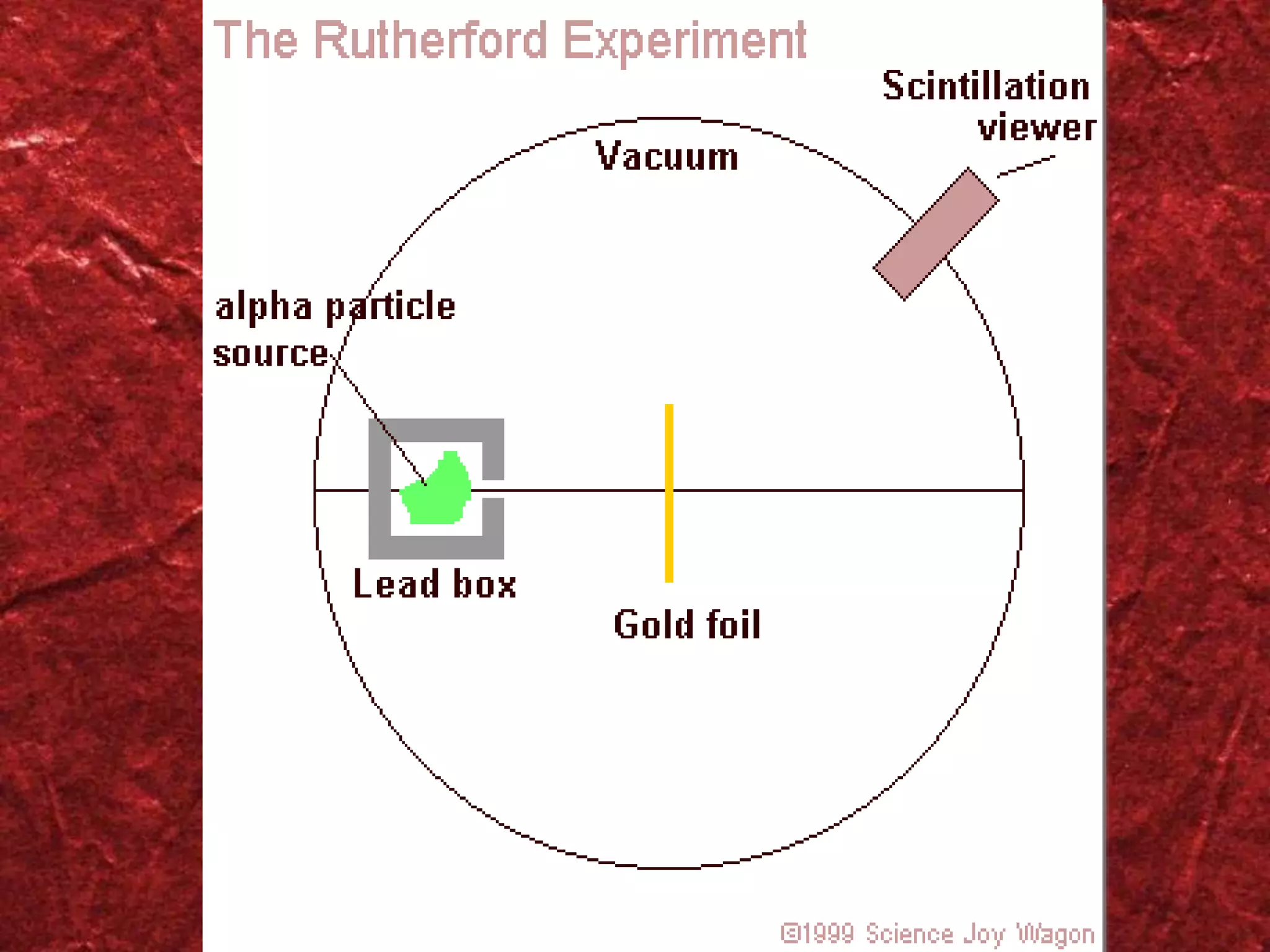
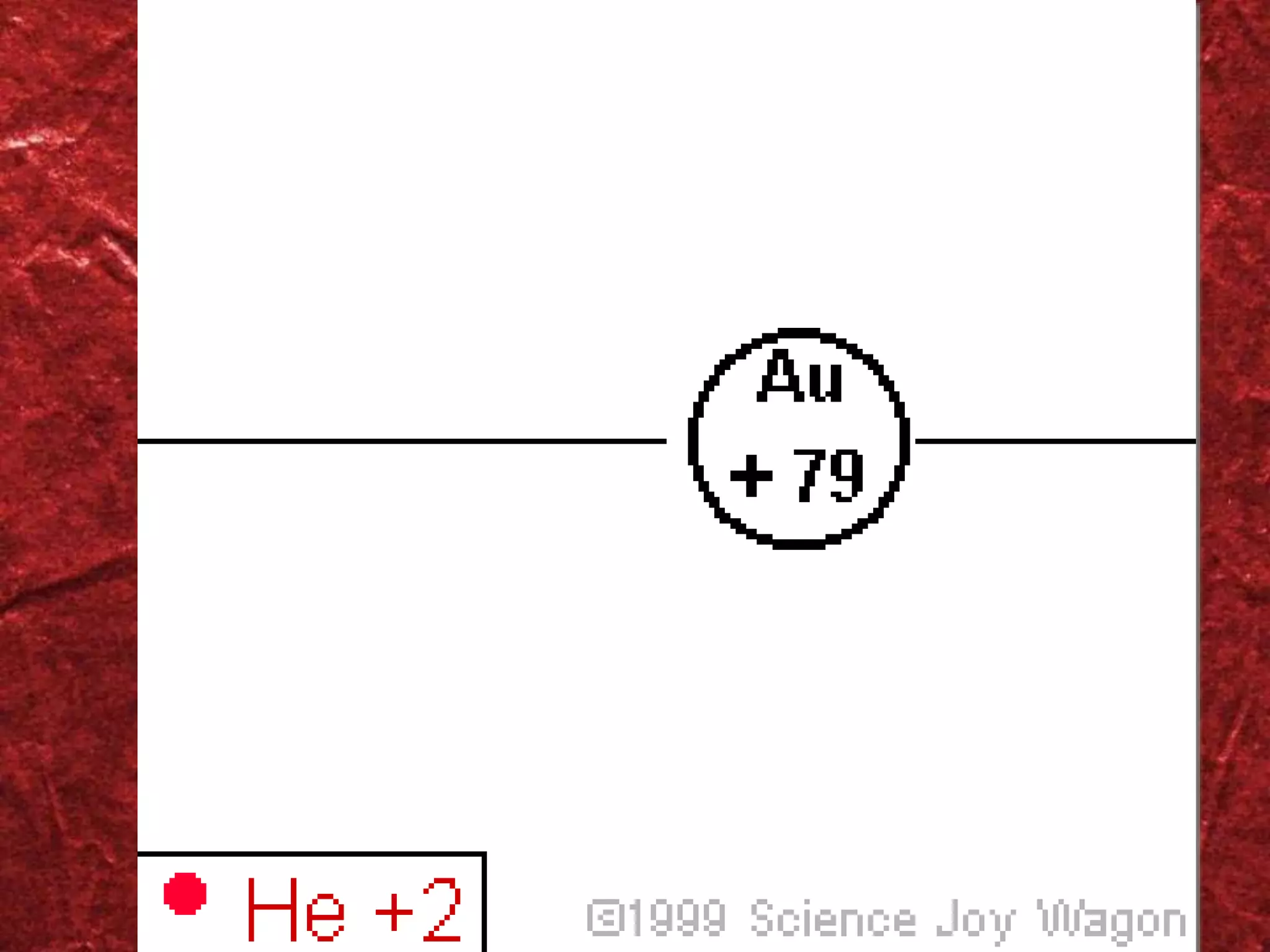
1) The atomic model has evolved over time as new evidence and theories emerged. Early models included the plum pudding model and Rutherford's model of a small, dense nucleus surrounded by electrons. 2) Bohr's model improved on this by proposing that electrons orbit the nucleus in fixed, quantized energy levels. Electrons absorb or emit photons of specific energies when changing levels. 3) Later, the wave mechanical model described electrons as existing in orbital regions rather than fixed orbits, depicted as electron clouds or probability distributions. This provides a more accurate quantum mechanical description of electrons in atoms.

1. Models of the Atom
• The impact of modern physics is most
evident in the development of the
atomic model of matter
• We use term atomic model to indicate
that we are trying to describe the key
features of the atom
• We do not know what an atom “looks
like”, because we have no instruments for
its direct observation.

2. Model of the Atom
• Ancient Greeks
• Matter is made up of particles,
but not the elements as we know
them today
• Four elemental substances
•Air, Fire, Earth, and Wind

3. A Change of Thought
• Robert Boyle (1600’s)
• Identified gold and silver as
being elemental
• In other words, they weren’t
made up of air, earth, fire, or
wind

4. Dalton’s Theory
• In 1700’s he theorized
that the basic unit of
matter is a tiny particle
called an atom.

5. Dalton’s Theory
• All elements are composed of
indivisible atoms
• All atoms of a given element
are identical
• Atoms of different elements
are different
• Compounds are formed by the
combination of atoms of
different elements

6. But Wait….
• Experimental studies of
the atom soon showed
that it (the atom) was not
indivisible… it has smaller
parts!

7. Thomson’s Model
• Just over 100 years ago, J.
J. Thomson discovered that
electrons are relatively low
mass, negatively charged
particles present in atoms

8. • Because he knew that
atoms were electrically
neutral, he concluded
that part of the atom
must posses positive
charge equal to the total
charge of the electrons

9. • He proposed a model in
which the atom consists of a
uniform distribution of
positive charge, in which
electrons are embedded
(like raisins in plum
pudding).
• “The Plum Pudding” Model

10. Rutherford’s Model

11. Rutherford’s Model
• Observations
• Most of the alpha particles pass
straight through the gold foil.
• Some of the alpha particles get
deflected by very small amounts.
• A very few get deflected greatly.
• Even fewer get bounced off the foil
and back to the left.

12. Rutherford’s Model
• Conclusions
• The atom is 99.99% empty space.
• The nucleus contains a positive
charge and most of the mass of
the atom.
• The nucleus is approximately
100,000 times smaller than the
atom.

13. Rutherford’s Model

14. The Bohr Model
• While the Rutherford model
focused on describing the nucleus,
Niels Bohr turned his attention to
describing the electron.

15. The Bohr Model
• Neils Bohr proposed a model
showing a dense nucleus
with electrons in
surrounding orbitals

17. The Bohr Model
• For electrons to stay in orbit,
they must have just the right
amount of energy to keep it in
place around the nucleus.

18. The Bohr Model
• The maximum number of electrons
in the first energy level is two.
• The second level has a maximum
of eight electrons.

19. The Wave Mechanical Model
• The major difference between the
wave-mechanical model and the
Bohr model is found in the manner
in which the electrons are
pictured.

20. The Cloud Model

21. The Wave Mechanical Model
• An orbital is described as a
region in which an electron
is most likely to be found.

22. The Structure of The Atom
• All atoms are composed of a
dense, positively charged
nucleus, surrounded by a
large space occupied by
electrons.

23. The Nucleus
• The nucleus contains two types
of particles
• Protons - with a positive charge
• Neutrons - with no charge

24. Subatomic Particles
• Protons have a mass of 1.67x10-24 g
• Because the mass is so small, we
sometimes use atomic mass units or
amu
• A proton is assigned 1 amu.
• A neutron is approx. the same

25. Subatomic Particles
• Each atom of a specific
element must contain the same
number of protons as each
other atom of that element.

26. Subatomic Particles
• The number of protons in
the nucleus of an atom is
the atomic number of that
element.

27. Subatomic Particles
• Electrons
• are much less massive than
either the proton or the neutron
• Have a charge equal to, but
opposite, a proton
• Occupy space outside the
nucleus
• Tape Demo

28. Subatomic Particles
• The sum of the numbers of
protons and neutrons in the
nucleus is called the mass
number.

29. Sample Problem
• Find the number of neutrons in an
atom of Selenium whose mass number
is 79.

30. Chemistry Humor
• A neutron walked into a
restaurant and asked how
much for a drink.
The waiter replied,
"for you, no charge."

31. Isotopes
• The atoms of a given
element must contain the
same number of protons,
but the number of neutrons
can vary.

32. Isotopes
• For Example: Most atoms of hydrogen
contain 1 proton and no neutrons
1
1H
• But some contain 1 proton and 1
neutron
1
2H
• Still others contain 1 proton and 2
neutrons
1
3H
• All three are still atoms of hydrogen

33. Isotopes
• Isotopes are atoms of the same
element that have different
numbers of neutrons
• Thus, they have different mass
numbers.

34. Isotope Symbols
• Isotopes can be identified by
using a symbol that indicates
both the element and its mass
number
• Examples
C-14 14C
Carbon-14 6
14C

35. Mass Number
• The mass number must be an
integer.
mass number = atomic number + neutrons

36. Atomic Masses
• Why are the atomic masses on the periodic
table fractional values (i.e. not integers)?
• Because… the atomic
masses are the average
mass of all the naturally
occurring isotopes in a
sample of the element

37. Sample Problem
• Atomic mass of carbon
• on overhead
• Lab - “Modeling Isotopes”
• Page
• Homework: Review Questions 13-20

38. Location of Electrons -
Energy Levels
• Each electron has its own distinct
amount of energy that corresponds
with the energy level it occupies.
• Electrons can gain or lose energy
and move to a different energy
level, but they do so in a unique
way….

39. • Electrons can only absorb a
“correct” amount of energy that
allows it to move to a higher
energy level
• These “packets of energy” are
photons of light.
• Different colors of light carry
different amounts of energy

41. • By convention there is
color,
by convention sweetness,
by convention bitterness,
but in reality there are
atoms and space. -
Democritus (400 BC)

42. Name this compound:
•Ba(Na)2
•answer: Banana.

43. •When electrons
occupy the lowest
available orbital,
the atom is said to
be in the ground
state.

44. • When electrons are
subject to heat, light, or
electricity, an electron
may absorb energy and
(temporarily) move to a
higher energy level. This
unstable condition is
called an excited state.

45. • When the electron returns to a
lower level it emits energy in the
form of infrared, ultraviolet, or
visible light.
• While the light appears as one
color to our eyes, it is actually
composed of many different
wavelengths (or colors of light)

46. • Because each atom has its
own distinct orbital energy
levels, each atom has its
own distinct pattern of
emission lines (also known
as bright line spectrum),
that can be used to identify
elements.
• Astronomy

47. The Bohr Model
• Bohr built upon spectroscopic
observations of atoms.
Spectroscopists noticed that an
atom can only absorb certain
energies (colors) of light (the
absorption spectrum) and once
excited can only release
certain energies (the emission
spectrum) and these energies
happen to be the same. Bohr
used these observations to
argue that the energy of a
bound electron is "quantized."
Absorption Spectrum
Emission Spectrum

48. The Bohr Model
• In the animation, you will see a model
of a Hydrogen atom and to the right
of it, a Bohr energy level diagram.
• In the animation you will notice that
if the energy of the photon of light is
just right, it will cause the electron to
jump to a higher level.
• When the electron jumps back down,
a photon is created for each jump
down.
• A photon without the right amount of
energy (the pink one) passes through
the atom with no effect.
• Photons with too much energy will
cause the electron to be ejected
which ionizes the atom. An ionized
electron is said to be in the n=infinity
energy level.
• Keep in mind that these rings are not
actually orbits, but are levels that
represent the location of an electron
wave. The number n corresponds to
the number of complete waves in the
electron.
Get out your reference tables and find the hydrogen
and mercury energy level diagrams.

49. The Bohr Model
• Ephoton = Einitial - Efinal (reference
tables)
• This formula can be used to determine the
energy of the photon emitted (+) or
absorbed(-).

50. Sample Problem
• Calculate the energy of the photon that is emitted when a
hydrogen atom changes from energy state n=3 to n=2. What color
corresponds with the photon emitted?
• Solution
• From reference tables…
E3 = Einitial = -1.51 eV
E2 = Efinal = -3.40 eV
Ephoton = Einitial – Efinal = (-3.40 eV) – (-1.51 eV) = -1.89 eV
Ephoton = hf ==== f = Ephoton / h
But we need Ephoton in Joules, because Planck’s constant is in Joules
Ephoton = (-1.89 eV) (1.60x10-19J / eV) = 3.02x10-19 J
f = (3.02x10-19 J) / (6.63x10-34 J∙s) = 4.56x1014 Hz
From reference tables, this frequency corresponds with red light.

51. The Bohr Model
• Summary of the Bohr Model
• All forms of energy are quantized. An electron can gain or lose
kinetic energy only in fixed amounts, or quanta.
• The electron in the hydrogen atom can occupy only certain specific
orbits of fixed radius and no others.
• The electron can jump from one orbit to a higher one by absorbing a
quantum of energy in the form of a photon.
• Each allowed orbit in the atom corresponds to a specific amount of
energy. The orbit nearest the nucleus represents the smallest amount
of energy that the electron can have.

52. Bohr Model Vocabulary
• When the electron is in the lowest energy
level (n=1), it is said to be in the ground
state.
• An electron in any level above the ground
state is said to be in an excited state.
• A spectral line is a particular frequency of
absorbed or emitted energy characteristic of
an atom

53. The Cloud Model
• The cloud model represents a sort
of history of where the electron
has probably been and where it is
likely to be going.
• The red dot in the middle
represents the nucleus while the
red dot around the outside
represents an instance of the
electron.
• Imagine, as the electron moves it
leaves a trace of where it
was. This collection of traces
quickly begins to resemble a
cloud.
• The probable locations of the
electron predicted by
Schrödinger's equation happen to
coincide with the locations
specified in Bohr's model.