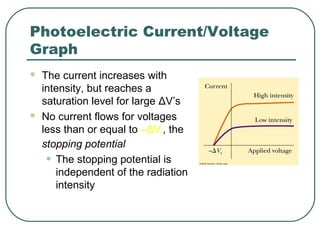
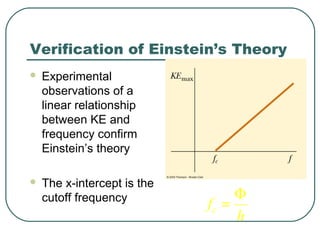
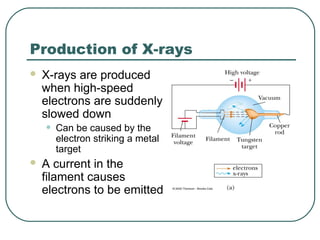
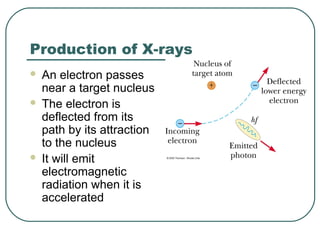
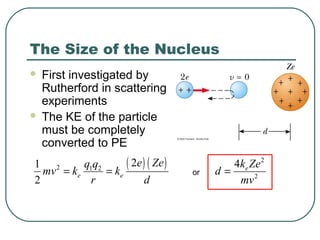
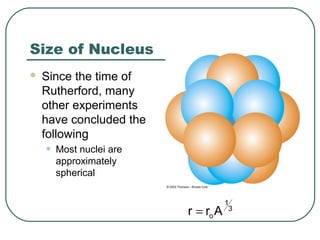
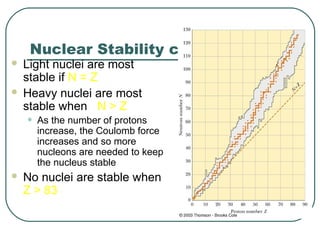
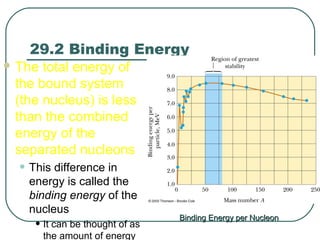
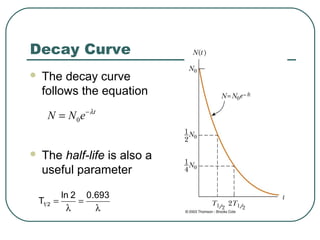
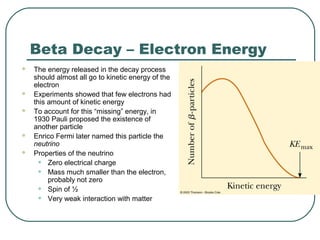
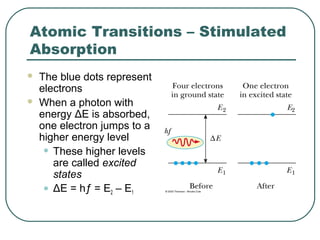
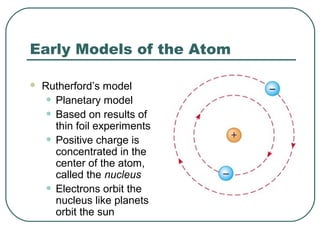
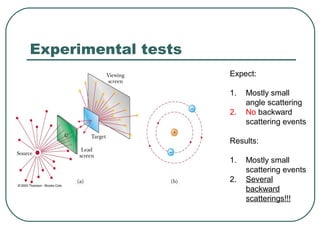
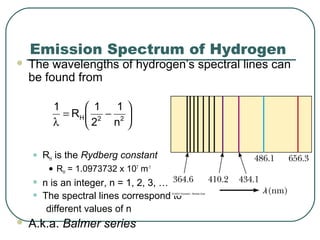
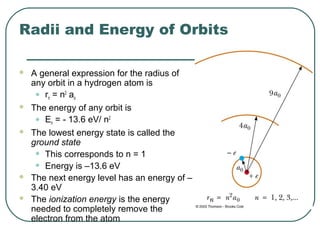
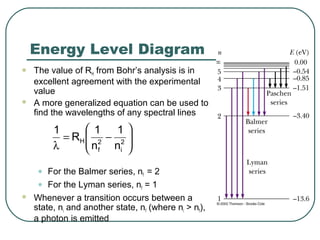
1. The document provides an overview and review of topics covered on the AP Physics B exam related to modern physics, including the photoelectric effect, Bohr model of the atom, and nuclear physics. 2. It describes Einstein's explanation of the photoelectric effect involving photons and how it resolved issues not explained by classical wave theory. 3. It also explains the Bohr model of the hydrogen atom, including Bohr's assumptions and how it leads to quantized electron orbits that can explain atomic emission spectra.

1. AP Phys B
Test Review
Modern Physics
5/9/2008

2. Overview
 Basics
 Photoelectric Effect
 Bohr Model of the atom
• Energy Transitions
 Nuclear Physics

3. Basics
 Quantization: the idea that light and
matter come in discreet, indivisible
packets
• Wave-particle duality in light and matter
• Matter behaves both as a wave and as a
particle.

4. Energy of a photon
 Blackbody radiation
• Ultraviolet catastrophe
• Planck came up with the idea that light is emitted by
certain discreet resonators that emit energy packets
called photons
• This energy is given by:
E h= ν

5. Photoelectric Effect Schematic
 When light strikes E,
photoelectrons are emitted
 Electrons collected at C and
passing through the ammeter
are a current in the circuit
 C is maintained at a positive
potential by the power supply

6. Photoelectric Current/Voltage
Graph
 The current increases with
intensity, but reaches a
saturation level for large ΔV’s
 No current flows for voltages
less than or equal to –ΔVs, the
stopping potential
• The stopping potential is
independent of the radiation
intensity

7. Features Not Explained by
Classical Physics/Wave Theory
 No electrons are emitted if the incident light
frequency is below some cutoff frequency that is
characteristic of the material being illuminated
 The maximum kinetic energy of the photoelectrons is
independent of the light intensity
 The maximum kinetic energy of the photoelectrons
increases with increasing light frequency
 Electrons are emitted from the surface almost
instantaneously, even at low intensities

8. Einstein’s Explanation
 A tiny packet of light energy, called a photon, would
be emitted when a quantized oscillator jumped from
one energy level to the next lower one
• Extended Planck’s idea of quantization to
electromagnetic radiation
 The photon’s energy would be E = hƒ
 Each photon can give all its energy to an electron in
the metal
 The maximum kinetic energy of the liberated
photoelectron is
KE = hƒ – Φ

9. Explanation of Classical
“Problems”
 The effect is not observed below a certain cutoff
frequency since the photon energy must be greater
than or equal to the work function
• Without this, electrons are not emitted, regardless
of the intensity of the light
 The maximum KE depends only on the frequency
and the work function, not on the intensity
 The maximum KE increases with increasing
frequency
 The effect is instantaneous since there is a one-to-
one interaction between the photon and the electron

10. Verification of Einstein’s Theory
 Experimental
observations of a
linear relationship
between KE and
frequency confirm
Einstein’s theory
 The x-intercept is the
cutoff frequency
cf
h
Φ
=

11. 27.4 X-Rays
 Electromagnetic radiation with short
wavelengths
• Wavelengths less than for ultraviolet
• Wavelengths are typically about 0.1 nm
• X-rays have the ability to penetrate most
materials with relative ease
 Discovered and named by Roentgen in
1895

12. Production of X-rays
 X-rays are produced
when high-speed
electrons are suddenly
slowed down
• Can be caused by the
electron striking a metal
target
 A current in the
filament causes
electrons to be emitted

13. Production of X-rays
 An electron passes
near a target nucleus
 The electron is
deflected from its
path by its attraction
to the nucleus
 It will emit
electromagnetic
radiation when it is
accelerated

14. 27.8 Photons and
Electromagnetic Waves
 Light has a dual nature. It exhibits both wave
and particle characteristics
• Applies to all electromagnetic radiation
 The photoelectric effect and Compton
scattering offer evidence for the particle nature
of light
• When light and matter interact, light behaves as if it
were composed of particles
 Interference and diffraction offer evidence of
the wave nature of light

15. 28.9 Wave Properties of
Particles
 In 1924, Louis de Broglie postulated that because
photons have wave and particle characteristics,
perhaps all forms of matter have both properties
 The de Broglie wavelength of a particle is
 The frequency of matter waves is
mv
h
=λ
h
E
=ƒ

16. The Davisson-Germer
Experiment
 They scattered low-energy electrons from a
nickel target
 The wavelength of the electrons calculated
from the diffraction data agreed with the
expected de Broglie wavelength
 This confirmed the wave nature of electrons
 Other experimenters have confirmed the wave
nature of other particles

17. 27.10 The Wave Function
 In 1926 Schrödinger proposed a wave equation that
describes the manner in which matter waves change
in space and time
 Schrödinger’s wave equation is a key element in
quantum mechanics
 Schrödinger’s wave equation is generally solved for
the wave function, Ψ
i H
t
∆Ψ
= Ψ
∆

18. The Wave Function
 The wave function depends on the
particle’s position and the time
 The value of |Ψ|2
at some location at a
given time is proportional to the
probability of finding the particle at that
location at that time

19. 27.11 The Uncertainty Principle
 When measurements are made, the
experimenter is always faced with
experimental uncertainties in the
measurements
• Classical mechanics offers no fundamental
barrier to ultimate refinements in
measurements
• Classical mechanics would allow for
measurements with arbitrarily small
uncertainties

20. The Uncertainty Principle
 Quantum mechanics predicts that a barrier to
measurements with ultimately small
uncertainties does exist
 In 1927 Heisenberg introduced the uncertainty
principle
• If a measurement of position of a particle is made
with precision Δx and a simultaneous measurement
of linear momentum is made with precision Δp, then
the product of the two uncertainties can never be
smaller than h/4π

21. The Uncertainty Principle
 Mathematically,
 It is physically impossible to measure
simultaneously the exact position and the
exact linear momentum of a particle
 Another form of the principle deals with
energy and time:
π
≥∆∆
4
h
px x
π
≥∆∆
4
h
tE

22. Early Models of the Atom
 Rutherford’s model
• Planetary model
• Based on results of
thin foil experiments
• Positive charge is
concentrated in the
center of the atom,
called the nucleus
• Electrons orbit the
nucleus like planets
orbit the sun

23. Experimental tests
Expect:
1. Mostly small
angle scattering
2. No backward
scattering events
Results:
1. Mostly small
scattering events
2. Several
backward
scatterings!!!

24. Difficulties with the Rutherford
Model
 Atoms emit certain discrete characteristic
frequencies of electromagnetic radiation
• The Rutherford model is unable to explain this
phenomena
 Rutherford’s electrons are undergoing a centripetal
acceleration and so should radiate electromagnetic
waves of the same frequency
• The radius should steadily decrease as this
radiation is given off
• The electron should eventually spiral into the
nucleus

25. 28.2 Emission Spectra
 A gas at low pressure
has a voltage applied to it
 When the emitted light is
analyzed with a
spectrometer, a series of
discrete bright lines is
observed
• Each line has a different
wavelength and color

26. Emission Spectrum of Hydrogen
 The wavelengths of hydrogen’s spectral lines can
be found from
• RH is the Rydberg constant
• RH = 1.0973732 x 107
m-1
• n is an integer, n = 1, 2, 3, …
• The spectral lines correspond to
different values of n
 A.k.a. Balmer series






−=
λ 22H
n
1
2
1
R
1

27. Absorption Spectra
 An element can also absorb light at specific
wavelengths
 An absorption spectrum can be obtained by
passing a continuous radiation spectrum through a
vapor of the gas
 The absorption spectrum consists of a series of
dark lines superimposed on the otherwise
continuous spectrum
• The dark lines of the absorption spectrum coincide with the
bright lines of the emission spectrum

28. 28.3 The Bohr Theory of
Hydrogen
 In 1913 Bohr provided an explanation of
atomic spectra that includes some features of
the currently accepted theory
 His model includes both classical and non-
classical ideas
 His model included an attempt to explain why
the atom was stable

29. Bohr’s Assumptions for
Hydrogen
 The electron moves in circular orbits
around the proton under the influence of
the Coulomb force of attraction
 Only certain electron orbits are stable
• These are the orbits in which the atom
does not emit energy in the form of
electromagnetic radiation
• Therefore, the energy of the atom
remains constant and classical
mechanics can be used to describe the
electron’s motion
 Radiation is emitted by the atom when the
electron “jumps” from a more energetic
initial state to a lower state
• The “jump” cannot be treated
classically
i fE E hf− =

30. Bohr’s Assumptions
 More on the electron’s “jump”:
• The frequency emitted in the “jump” is related
to the change in the atom’s energy
• It is generally not the same as the frequency
of the electron’s orbital motion
 The size of the allowed electron orbits is determined
by a condition imposed on the electron’s orbital
i fE E hf− = , 1,2,3,...
2
e
h
m vr n n
π
 
= = ÷
 

31. Results
 The total energy of the atom
•
 Newton’s law
 This can be used to rewrite kinetic energy as
2
21
2
e e
e
E KE PE m v k
r
= + = −
r2
ek
E
2
e
−=
2 2
2e e e
e v
F m a or k m
r r
= =
2 2
2 2
e
mv e
KE k
r
≡ =

32. Bohr Radius
 The radii of the Bohr orbits are quantized
• This shows that the electron can only exist in
certain allowed orbits determined by the integer n
•When n = 1, the orbit has the smallest radius,
called the Bohr radius, ao
•ao = 0.0529 nm


,3,2,1n
ekm
n
r 2
ee
22
n ==
2
h
π=

33. Radii and Energy of Orbits
 A general expression for the radius of
any orbit in a hydrogen atom is
• rn = n2
ao
 The energy of any orbit is
• En = - 13.6 eV/ n2
 The lowest energy state is called the
ground state
• This corresponds to n = 1
• Energy is –13.6 eV
 The next energy level has an energy of –
3.40 eV
 The ionization energy is the energy
needed to completely remove the
electron from the atom

34. Energy Level Diagram
 The value of RH from Bohr’s analysis is in
excellent agreement with the experimental
value
 A more generalized equation can be used to
find the wavelengths of any spectral lines
• For the Balmer series, nf = 2
• For the Lyman series, nf = 1
 Whenever a transition occurs between a
state, ni and another state, nf (where ni > nf),
a photon is emitted






−=
λ 2
i
2
f
H
n
1
n
1
R
1

35. Quantum Number Summary
 The values of n can increase from 1 in integer steps
 The values of ℓ can range from 0 to n-1 in integer steps
 The values of mℓ can range from -ℓ to ℓ in integer steps

36. Atomic Transitions – Energy
Levels
 An atom may have
many possible energy
levels
 At ordinary
temperatures, most of
the atoms in a sample
are in the ground state
 Only photons with
energies corresponding
to differences between
energy levels can be
absorbed

37. Atomic Transitions – Stimulated
Absorption
 The blue dots represent
electrons
 When a photon with
energy ΔE is absorbed,
one electron jumps to a
higher energy level
• These higher levels
are called excited
states
• ΔE = hƒ = E2 – E1

38. Atomic Transitions –
Spontaneous Emission
 Once an atom is in
an excited state,
there is a constant
probability that it will
jump back to a lower
state by emitting a
photon
 This process is
called spontaneous
emission

39. Atomic Transitions – Stimulated
Emission
 An atom is in an excited
stated and a photon is
incident on it
 The incoming photon
increases the
probability that the
excited atom will return
to the ground state
 There are two emitted
photons, the incident
one and the emitted
one

40. 29.1 Some Properties of Nuclei
 All nuclei are composed of protons and neutrons
• Exception is ordinary hydrogen with just a proton
 The atomic number, Z, equals the number of
protons in the nucleus
 The neutron number, N, is the number of neutrons
in the nucleus
 The mass number, A, is the number of nucleons in
the nucleus
• A = Z + N
• Nucleon is a generic term used to refer to either a proton or
a neutron
• The mass number is not the same as the mass

41. Charge and mass
Charge:
 The electron has a single negative charge, -e (e = 1.60217733 x 10-19
C)
 The proton has a single positive charge, +e
• Thus, charge of a nucleus is equal to Ze
 The neutron has no charge
• Makes it difficult to detect
Mass:
 It is convenient to use atomic mass units, u, to express masses
• 1 u = 1.660559 x 10-27
kg
 Mass can also be expressed in MeV/c2
• 1 u = 931.494 MeV/c2

42. The Size of the Nucleus
 First investigated by
Rutherford in scattering
experiments
 The KE of the particle
must be completely
converted to PE
2
2
4 ek Ze
d
mv
=
( ) ( )2 1 2
21
2
e e
e Zeq q
mv k k
r d
= = or

43. Size of Nucleus
 Since the time of
Rutherford, many
other experiments
have concluded the
following
• Most nuclei are
approximately
spherical
3
1
oArr =

44. Density of Nuclei
 The volume of the nucleus (assumed to be
spherical) is directly proportional to the total
number of nucleons
 This suggests that all nuclei have nearly the
same density
 Nucleons combine to form a nucleus as
though they were tightly packed spheres

45. Nuclear Stability
 There are very large repulsive electrostatic forces
between protons
• These forces should cause the nucleus to fly apart
 The nuclei are stable because of the presence of
another, short-range force, called the nuclear (or
strong) force
• This is an attractive force that acts between all nuclear
particles
• The nuclear attractive force is stronger than the Coulomb
repulsive force at the short ranges within the nucleus

46. Nuclear Stability chart
 Light nuclei are most
stable if N = Z
 Heavy nuclei are most
stable when N > Z
• As the number of protons
increase, the Coulomb force
increases and so more
nucleons are needed to keep
the nucleus stable
 No nuclei are stable when
Z > 83

47. Isotopes
 The nuclei of all atoms of a particular element must contain
the same number of protons
 They may contain varying numbers of neutrons
• Isotopes of an element have the same Z but differing N
and A values
C11
6
C14
6C13
6C12
6

48. 29.2 Binding Energy
 The total energy of
the bound system
(the nucleus) is less
than the combined
energy of the
separated nucleons
• This difference in
energy is called the
binding energy of the
nucleus
• It can be thought of as
the amount of energy
Binding Energy per NucleonBinding Energy per Nucleon

49. Binding Energy Notes
 Except for light nuclei, the binding energy is
about 8 MeV per nucleon
 The curve peaks in the vicinity of A = 60
• Nuclei with mass numbers greater than or less than 60
are not as strongly bound as those near the middle of
the periodic table
 The curve is slowly varying at A > 40
• This suggests that the nuclear force saturates
• A particular nucleon can interact with only a limited
number of other nucleons

50. 29.3 Radioactivity
 Radioactivity is the spontaneous
emission of radiation
 Experiments suggested that radioactivity
was the result of the decay, or
disintegration, of unstable nuclei
 Three types of radiation can be emitted
• Alpha particles
• The particles are 4
He nuclei
• Beta particles
• The particles are either electrons or positrons

51. Distinguishing Types of
Radiation
 The gamma particles
carry no charge
 The alpha particles are
deflected upward
 The beta particles are
deflected downward
• A positron would be
deflected upward

52. Penetrating Ability of Particles
 Alpha particles
• Barely penetrate a piece of paper
 Beta particles
• Can penetrate a few mm of aluminum
 Gamma rays
• Can penetrate several cm of lead

53. The Decay Constant
 The number of particles that decay in a given
time is proportional to the total number of
particles in a radioactive sample
• λ is called the decay constant and determines the rate
at which the material will decay
 The decay rate or activity, R, of a sample is
defined as the number of decays per second
N
R N
t
λ
∆
= =
∆ ( )N N tλ∆ = − ∆

54. Decay Curve
 The decay curve
follows the equation
 The half-life is also a
useful parameter
λ
=
λ
=
693.02ln
T 21
0
t
N N e λ−
=

55. Units
 The unit of activity, R, is the Curie, Ci
• 1 Ci = 3.7 x 1010
decays/second
 The SI unit of activity is the Becquerel,
Bq
• 1 Bq = 1 decay / second
• Therefore, 1 Ci = 3.7 x 1010
Bq
 The most commonly used units of
activity are the mCi and the µCi

56. Alpha Decay
 When a nucleus emits an alpha particle it
loses two protons and two neutrons
• N decreases by 2
• Z decreases by 2
• A decreases by 4
HeYX 4
2
4A
2Z
A
Z +→ −
−

57. Beta Decay
 During beta decay, the daughter nucleus has the
same number of nucleons as the parent, but the
atomic number is one less
 In addition, an electron (positron) was observed
 The emission of the electron is from the nucleus
• The nucleus contains protons and neutrons
• The process occurs when a neutron is
transformed into a proton and an electron
• Energy must be conserved

58. Beta Decay – Electron Energy
 The energy released in the decay process
should almost all go to kinetic energy of the
electron
 Experiments showed that few electrons had
this amount of kinetic energy
 To account for this “missing” energy, in
1930 Pauli proposed the existence of
another particle
 Enrico Fermi later named this particle the
neutrino
 Properties of the neutrino
• Zero electrical charge
• Mass much smaller than the electron,
probably not zero
• Spin of ½
• Very weak interaction with matter

59. Gamma Decay
 Gamma rays are given off when an excited nucleus “falls” to a lower
energy state
• Similar to the process of electron “jumps” to lower energy states and
giving off photons
 The excited nuclear states result from “jumps” made by a proton or neutron
 The excited nuclear states may be the result of violent collision or more
likely of an alpha or beta emission
 Example of a decay sequence
• The first decay is a beta emission
• The second step is a gamma emission
γ+→
ν++→ −
C*C
e*CB
12
6
12
6
12
6
12
5