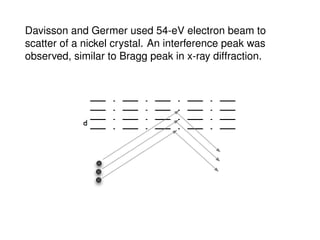
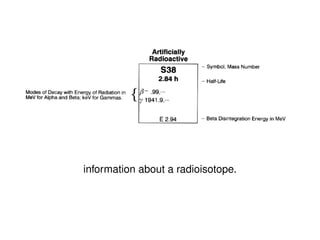
The document provides a comprehensive overview of basic nuclear physics, including historical developments, atomic models, nuclear reactions, and radiation types. Key concepts such as decay laws, quantum mechanics, and particle interactions are discussed along with experimental validations and notable discoveries in the field. Additionally, it covers the behavior of electrons, nuclear decay processes, and generating radionuclides, providing a foundational understanding of nuclear physics principles.

1. Basic Nuclear Physics
Roppon Picha
created: November 2005
updated: April 8, 2010

2. Dalton’s atoms (1808)

3. J.J. Thomson’s Experiment
cathode rays = electrons (1897)

4. Rutherford, Geiger, Marsden
226 222 218
88 Ra → 86 Rn +α → α + 84 Po

5. rate of alpha scattering at angle θ from nucleus of charge
Z:
2
Ze2 1
R(θ) ∝ 2 4
mα vα sin (θ/2)

6. Electron configuration
Rutherford model (1911): Electrons orbit the nucleus like
planets orbit the Sun.
Bohr model of the atom (1913): Electrons stay in the
atom on special orbits (orbitals).
Experimentally verified by James Franck and Gustav
Ludwig Hertz in 1914. Atoms only absorb certain
“chunks” of energy.

7. Electron configuration
principal quantum number: n = 1, 2, 3, . . .
e− most strongly bound at n = 1.
example: sodium (Na) has 11 electrons. In ground state,
2 electrons are in n = 1 level, 8 in n = 2, and 1 in n = 3.

8. Hydrogen
e2 1
V (r ) = −
4π 0 r
13.6
En = − eV
n2
(Bohr formula, 1913)
hydrogenic (1 electron, Ze nuclear charge):
13.6Z 2
En = −
n2

9. Sub configurations
Besides n, we have orbital angular momentum
quantum number l.
l = 0, 1, 2, . . . , n − 1
letters: s, p, d, f, g, h, . . .
Then, there is spin quantum number s.

10. Quantum angular momentum
total angular momentum quantum number j:
j=s+l
values jump in integer steps:
|l − s| ≤ j ≤ l + s

11. Quantum angular momentum
example:
for the electron, s = 1/2. if l = 1, what are possible values
of j?
s = 1/2 and l = 3?
What are all possible j values for electron in n = 4 level?

12. Proton (1919) was discovered by Rutherford.
α+N→H+O
Protos = first

13. Chadwick’s Neutron Discovery
• Existence suggested since 1920 by Rutherford.
• Finally found via experiments in 1932.
9
4 Be5 +4 He2+
2 2 −→ 12
6 C +1 n1
0
or (α, n) reaction
mass: neutron 939.6 MeV/c2 ≈ proton 938.3 MeV/c2

14. Neutron energy
Fast neutrons = high-energy neutrons. E > 1 eV.
Thermal neutrons = those with average thermal energy
corresponding to room temperature (T = 300 K).
3 1
Eth = kB T ≈ eV
2 40
where kB = 1.38 × 10−23 J/K.

15. Energy and Velocity
For a nucleon of kinetic energy 15 MeV, the velocity can
be calculated via
1
T = mv 2
2
2T 2 · 15
v= ≈c ≈ 0.18c
m 938
de Broglie wavelength of this nucleon is
h 4.1 × 10−21 MeV s
λ= = ≈ 7.3 fm
mv 938MeV c−2 · 0.18c

16. Accelerated Charge

17. EM radiation
Electric field far away does not know of particle’s
movement.
The electric field form a wavefront consisting radial
(Coulomb) and transverse components.
q 2 a2
radiated power = P = Larmor’s equation
6π 0 c 3

18. Electromagnetic Spectrum

19. p++

20. Region of Stability

21. Binding Energy per Nucleon

22. Binding energy
binding energy of most nuclei ∼ 8 MeV/nucleon
electrons are bound at ∼ 10 eV to atoms.

23. Separation Energy
removing a proton:
A A−1
Z XN −→ Z −1 YN
removing a neutron:
A A−1
Z XN −→ Z YN−1
Separation energy (S) is the difference between binding
energies (B) of initial nucleus and final nucleus.

24. Separation Energy
S > 0 when we change a stable nucleus (high B) into a
less stable nucleus (low B).
B = ( mconstituents − matom )c 2
S ≡ Bi − Bf
Sp = B(A XN ) − B(A−1 YN )
Z Z −1
Sn = B(A XN ) − B(A−1 YN−1 )
Z Z

25. Ionization vs. Separation

26. Quantum behaviors
Subatomic particles can be described by quantum
mechanics.
States are represented by wave function ψ(x, t).
Particles = Wave packets = superpositions of waves.

27. Wave functions
Wave = non-localized state.
∆x · ∆p >
(Heisenberg uncertainty relation)
To get the wave function and its evolution, solve
Schrodinger’s equation:
2
∂ψ
i = − +V ψ
∂t 2m

28. Wave function
Normalization:
∞
|ψ(x, t)|2 dx = 1
−∞
At any given time, the particle has to be somewhere.
expectation values:
x = ψ ∗ (x)ψ dx
p = ψ ∗ (p)ψ dx

29. Wave properties
de Broglie wavelength of a (non-zero mass) particle of
momentum p
h
λ=
p
Experimental verification: Davisson and Germer (1954).

30. Davisson and Germer used 54-eV electron beam to
scatter of a nickel crystal. An interference peak was
observed, similar to Bragg peak in x-ray diffraction.

32. Photons
∼ 1900: Blackbody radiation study led Planck to think
about nature of electromagnetic energy.
1905: Einstein proposed that light consists of photons,
each possessing a certain lump of energy.
Total energy = multiples of this number.

33. Energy
Planck-Einstein relation gives energy of a photon:
hc
E = hν = ω =
λ
ν and ω are frequency and angular frequency,
respectively.

34. Energy
h = 6.63 × 10−34 J s = 4.14 eV s
for λ given in angstrom:
12.4
E= keV
λ
Characteristic radiation of atoms which has only certain
values are due to the fact that the atoms only exist in
certain stable states of discrete energies.

35. Photon interactions
excitation (and de-excitation)
hν + Am ↔ An
ionization (and recombination)
hν + A ↔ A+ + e−

36. Fermions and Bosons
Protons, neutrons, and electrons belong to the fermion
family.
Quarks and leptons are also fermions.
They have odd half-integer spins: s = 1/2, 3/2, 5/2, . . ..
Bosons have integer spin: s = 0, 1, 2, . . ..
examples: photons (s = ±1) and 4 He atoms (s = 0)

37. Periodic table
Electrons are identical fermions. At a given orbital
(n, l, m), only two electrons can occupy the same state
(one spin-up, one spin-down)
For each l, there are 2l + 1 values of ml . For each (l, ml ,
there is two spin states (ms = ± 1 ).
2
Exercise: What are maximum number of electrons for
l = 0, 1, 2, 3?

38. Periodic table shows an integer increase of protons and
electrons. Shells are filled, from low to high energies.
Ground-state configs:
• H: (1s 1 )
• He: (1s 2 )
• Li: (He)(2s 1 )
• Be: (He)(2s 2 )
• B: (He)(2s 2 )(2p 1 )
• ...

39. information about a radioisotope.

42. Decay Law
dN(t)
= −λN(t)
dt
t is time. N(t) is number of nuclei. λ is decay constant.
solution:
N(t) = N0e−λt
N0 = number of nuclei at the starting time.
decay constant is inversely proportional to the half-life:
ln 2
λ=
t1/2

43. A parent nuclide decays and yields a daughter nuclide.
increase in number of daughter (D) = decrease in number
of parents (P)
Df − Di = Pi − Pf

44. Decay constant
Decays aren’t always 1-to-1:
A → B (55% of the time)
→ C (40%)
→ D (5%)
For branched decays, the total decay constant is just the
sum of each mode constant:
λtot = λ1 + λ2 + λ3 + . . .

45. Lifetime
For a given decay constant λ, the lifetime of the state is
1
τ=
λ
It is the time taken the state to drop from N0 to
N0 /e ≈ 0.37N0 .
branched decays:
1
τ=
λ1 + λ2 + . . .

46. Activity
dN
A≡− = λN = −λN0 e−λt = A0 e−λt
dt
A is also called “decay rate” or “disintegration rate.”
units: becquerel (1 s−1 ) or curie (3.7 × 1010 s−1 )

47. Mysterious rays
Henri becquerel discovered radioactivity from uranium ore
in 1896.
At Cambridge, Rutherford studied these unknown rays
and published results in 1899.
Those that got absorbed by a sheet of paper or a few cm
of air was named alpha rays.
The more penetrating ones were called beta rays.

48. Alpha Decay
Alpha (α) = 2p&2n bound state
Process:
A A−4
Z XN −→ Z −2 YN−2 + 4 He2
2

49. Examples:
226 222
88 Ra138 → 86 Rn136 + α
238 234
92 U146 → 90 Th144 + α
mX c 2 = (mY c 2 + TY ) + (mα c 2 + Tα )
Q ≡ (mi − mf )c 2 = (mX − mY − mα )c 2

50. Alpha emitters with large Q tend to have short half-lives.
Z
ln λ(E) = a − b √
E
Geiger-Nuttall law. λ is the decay constant; a and b are
constants; Z is the atomic number; E is the decay energy.

51. Beta Decay
W. Pauli: There must be a neutrino. (1930)
Cowan and Reines observed it. (1956)

52. Beta Decay
Processes:
n → p + e− + νe
¯ β − decay
p → n + e+ + νe β + decay (rare)
p + e− → n + νe e capture (ε)
Examples:
234 234 −
90 Th144 → 91 Pa143 + e + νe
¯
53m 53 +
27 Co → 26 Fe + e + νe
15 − 15
O+e → N + νe

53. X-ray
Charged particles that decelerate create electromagnetic
radiation. This process is known as bremsstrahlung.
Photons can excite or ionize atoms.
Subsequent atomic transitions can produce additional
X-ray photons. This process is called X-ray
fluorescence.
If an atomic electron absorbs such X-ray photon, it can be
ejected. These electrons are called Auger (oh-zhay)
electrons.

55. Gamma Decay
A year after Rutherford discovered α and β rays, Paul
Villard discovered a more penetrating radiation from
radium. This is the gamma (γ) ray.
Excited nuclear states can decay via γ emission. Typical
energies ∼ 0.1 − 10 MeV.
Examples:
99m 99
43 Tc → 43 Tc + γ isomeric transition
−
60
27 Co → 60
28 Ni + e + νe + γ
¯ with β −

56. Internal conversion
An excited nucleus can interact with an orbital electron,
transferring energy Eex .
The electron gets ejected with energy
Ee = Eex − Eb
where Eb is the binding energy of the electron.

58. The gamma decay and internal conversion decay
contribute to total decay probability:
λ = λγ + λe

59. Radiation Units
quantity description units
activity (A) decay rate curie (Ci), becquerel (Bq)
exposure (X ) air ionization roentgen (R), coulomb/kg
absorbed dose (D) absorbed energy rad, gray (Gy)
dose equivalent (DE) bio. effects rem, sievert (Sv)

60. Quiz
1. What kind of radiation does not come from a
nucleus? [choices: α, β, x-ray, γ]
2. Be-7 decays by capturing an electron. What is the
resulting nuclide?
3. 15.1% of natural samarium is 147 Sm, which decays by
emitting α. 10 grams of natural samarium gives 120 α
per second. Calculate activity per gram of 147 Sm.

61. Reaction Cross Section
for reaction
a + X −→ Y + b
reaction rate
σ=
fluxincident · densitytarget
rate of detecting b
=
(flux of a) · (X areal density)

62. Nuclear Reactions: First reaction in lab

63. Creating new nuclides
making light radionuclides:
14
N + n →14 C +1 H
55
Mn +2 H →55 Fe + 2n
59
Co + n →60 Co + γ
making Np-239 (transuranic)
238
U + n →239 U
239
U →239 Np + e− + νe
¯

64. Balancing nuclear equations
What is x in each of these nuclear reactions?
197 12
79 Au +6 C → 206At + x
85
32 4
16 S + He → x +γ
27
13 Al + p → x +n
4
He +17 N
7 → x +1 H

65. EM interactions
Main processes:
Photoelectric absorption
Compton scattering
Pair production

66. Intensity attenuation:
I(x) = I(0)e−µx
half-value layer = thickness that reduces intensity by 50%.

67. Producing radionuclides
Ways to do it:
• Reactors
• Accelerators
• Generators

68. Reactors
A
X +n → →
Longer irradiation time → higher specific activity.

69. Examples:
130
51 Te +n → →
6
3 Li +n →α+t
as fission products:
85 133 90 99 137
36 Kr, 54 Xe, 38 Sr, 42 Mo, 55 Cs

70. Accelerators
Usual projectiles: p, d, α
Examples:
20 18
10 Ne(d, α) 9 F
76 76
34 Se(p, n) 35 Br
35 38
17 Cl(α, n) 19 K

71. Generators
Suppose you want to use a short-lived nuclide produced
from a reactor. But you are far away from the reactor.
What can you do?
Prepare the parent nuclide which has longer half-life, in a
device that can separate the daughter from the parent.
Examples:
44 44
22 Ti (t1/2 = 6 y) ⇒ 21 Sc (t1/2 = 3.9 h)
83 83m
37 Rb (86 d) ⇒ 36 Kr (1.8 h)
99 99m
42 Mo (66 h) ⇒ 43 Tc (6 h)

72. the End