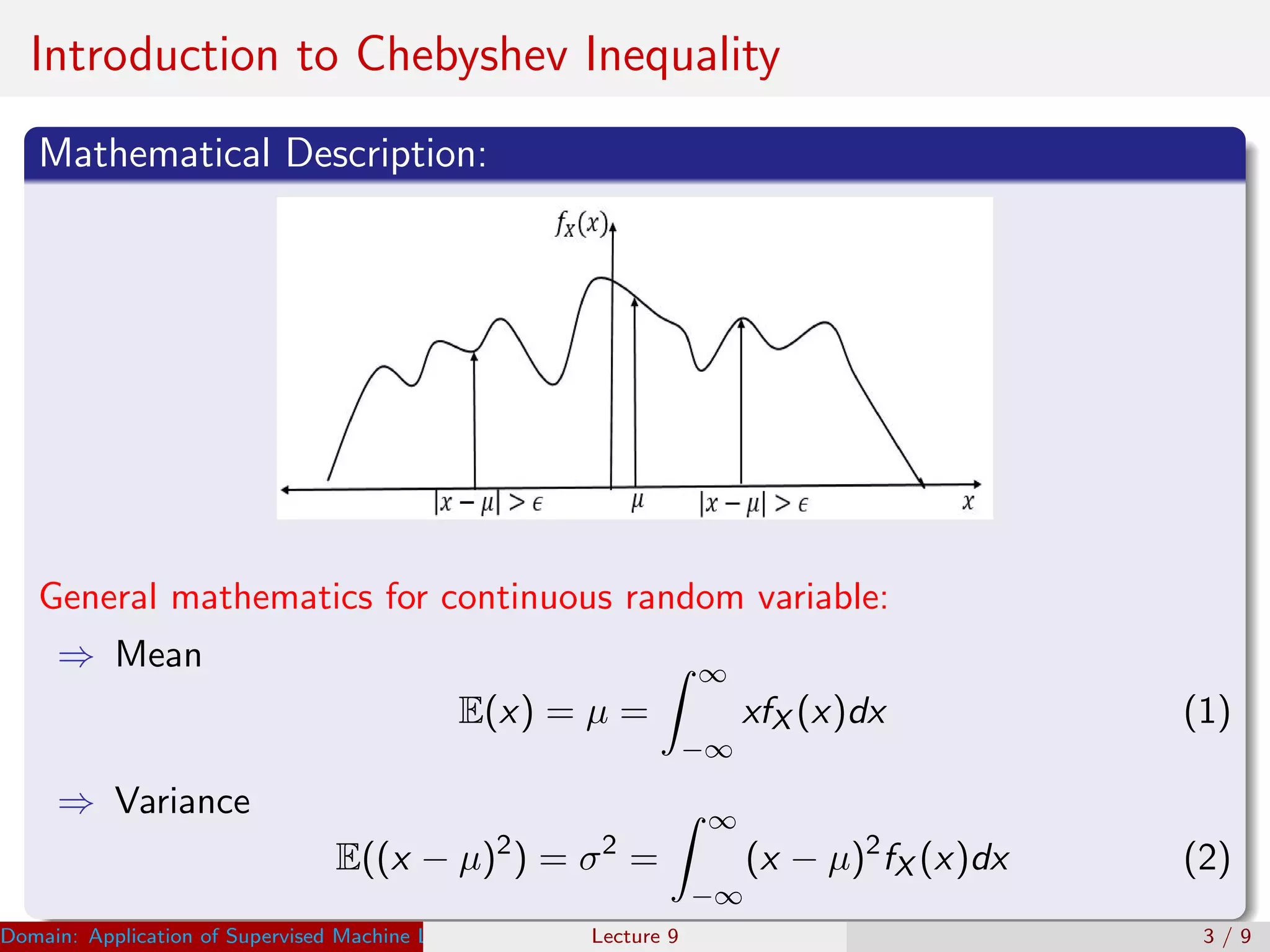
This document discusses the application of Chebyshev and Markov inequalities in supervised machine learning. It introduces the mathematical descriptions of Chebyshev and Markov inequalities and how they can be used to find the probability of new data falling within or outside a threshold value. Supervised learning is also introduced as learning from predefined training data to develop a model that can then be used to classify new data. The inequalities help in making decisions by defining favorable and non-favorable regions and allowing the probability of new data to be predicted based on the variance or mean of the training data.

1. Application of Chebyshev and Markov Inequality in
Supervised Machine Learning
Domain: Application of Supervised Machine Learning
Dr. Varun Kumar
Domain: Application of Supervised Machine Learning Dr. Varun Kumar (IIIT Surat)Lecture 9 1 / 9

2. Outlines
1 Introduction to Chebyshev Inequality
2 Introduction to Markov Inequality
3 Introduction to Supervised Learning
4 Application of these Inequalities in Supervised Machine Learning
5 References
Domain: Application of Supervised Machine Learning Dr. Varun Kumar (IIIT Surat)Lecture 9 2 / 9

3. Introduction to Chebyshev Inequality
Mathematical Description:
General mathematics for continuous random variable:
⇒ Mean
E(x) = µ =
∞
−∞
xfX (x)dx (1)
⇒ Variance
E((x − µ)2
) = σ2
=
∞
−∞
(x − µ)2
fX (x)dx (2)
Domain: Application of Supervised Machine Learning Dr. Varun Kumar (IIIT Surat)Lecture 9 3 / 9

4. Chebyshev inequality
∞
−∞
(x − µ)2
fX (x)dx ≥
|x−µ|≥
(x − µ)2
fX (x)dx (3)
Taking the minimum value, i.e |x − µ| = → Finite deviation
|x−µ|≥
(x − µ)2
fX (x)dx =
|x−µ|≥
2
fX (x)dx = 2
P(X − µ ≥ ) (4)
From (2) and (4)
2
P(X − µ ≥ ) ≤ σ2
⇒ P(X − µ ≥ ) ≤
σ2
2
(5)
Case 1: when = nσ
P(X − µ ≥ ) = P(X − µ ≥ nσ) ≤
1
n2
(6)
Domain: Application of Supervised Machine Learning Dr. Varun Kumar (IIIT Surat)Lecture 9 4 / 9

5. Continued–
As per the properties of probability, P(X ≤ µ) + P(X ≥ µ) = 1. Hence,
P(X − µ ≤ ) ≤ 1 −
σ2
2
⇒ P(X − µ ≤ nσ) ≤ 1 −
1
n2
(7)
For discrete random variable:
Mean
E(x) = µ =
∞
i=−∞
xi PX (xi ) (8)
Variance
Var(x) = σ2
= E (x − µ)2
=
∞
i=−∞
(xi − E(x))2
PX (xi ) (9)
PX (.) → Probability mass function.
Domain: Application of Supervised Machine Learning Dr. Varun Kumar (IIIT Surat)Lecture 9 5 / 9

6. Markov inequality
P(X − µ ≤ ) ≤ 1 −
σ2
2
⇒ P(X − µ ≤ nσ) ≤ 1 −
1
n2
(10)
Markov inequality
Statement: If X is a positive random variable, i.e X > 0, having probability
density function fX (x). Let a is an positive arbitrary constant, then
P(X ≥ a) ≤
E(x)
a
(11)
Proof: As per the properties of random variable,
E(x) =
∞
0
xfX (x)dx ≥
∞
a
xfX (x)dx
Let x = a, then ⇒ E(x) ≥
∞
a
xfX (x)dx ≥
∞
a
afX (x)dx = aP(X > a)
Domain: Application of Supervised Machine Learning Dr. Varun Kumar (IIIT Surat)Lecture 9 6 / 9

7. Introduction to supervised learning
Supervised learning
1 It is a method of learning, where some set of predefined training data
is available.
2 Based on these training data or sequence, a mathematical or logical
model is developed.
3 This training data sequence or developed model through these data
acts as a supervisor.
4 When new data comes then it is expected that the data will follow
the developed model.
5 For developing a model through these training data, we may utilize
some well defined statistical, mathematical or logical model.
6 Those model gives a minimum mean square error value, that may be
selected as a most suitable model.
Domain: Application of Supervised Machine Learning Dr. Varun Kumar (IIIT Surat)Lecture 9 7 / 9

8. Relation between supervised learning and inequality
1. Decision action plays an important role in machine learning.
2. Inequality relation helps for making a decision favorable or
non-favorable region.
3. Statistical framework helps for modeling the synthetic data that is
nothing but the theoretical bound.
4. Applying Chebyshev inequality, there is requirement of variance of the
data sequence. It is independent from the type of distribution.
5. From relation (7) and (10), we can predict or find the probability of
any real world new data that is above or below some threshold value.
6. Applying Markov inequality, only mean value is required for finding
probability. It also independent from density function.
Domain: Application of Supervised Machine Learning Dr. Varun Kumar (IIIT Surat)Lecture 9 8 / 9

9. References
J. Navarro, “A very simple proof of the multivariate chebyshev’s inequality,”
Communications in Statistics-Theory and Methods, vol. 45, no. 12, pp. 3458–3463,
2016.
M. I. Jordan and T. M. Mitchell, “Machine learning: Trends, perspectives, and
prospects,” Science, vol. 349, no. 6245, pp. 255–260, 2015.
Domain: Application of Supervised Machine Learning Dr. Varun Kumar (IIIT Surat)Lecture 9 9 / 9