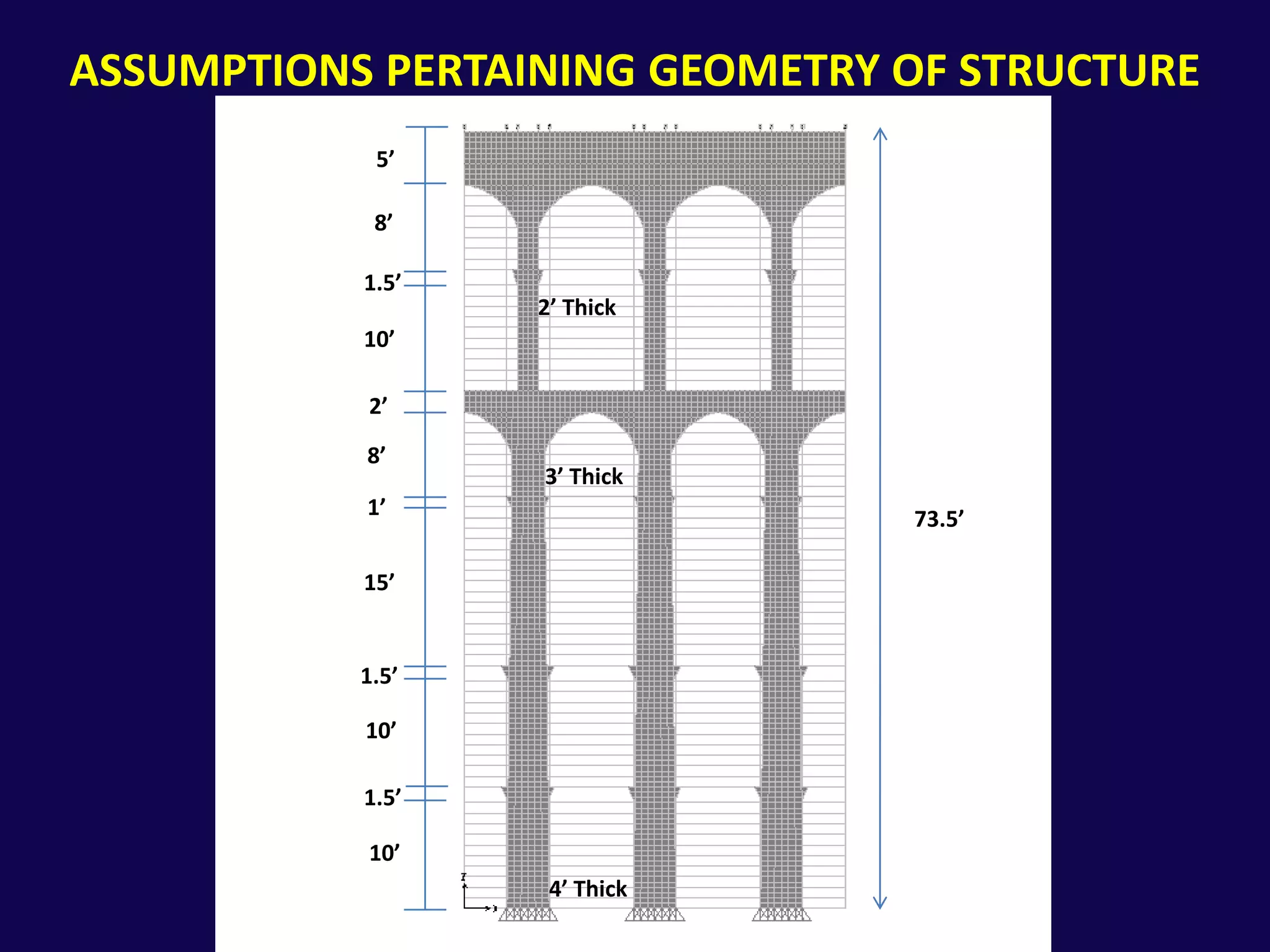
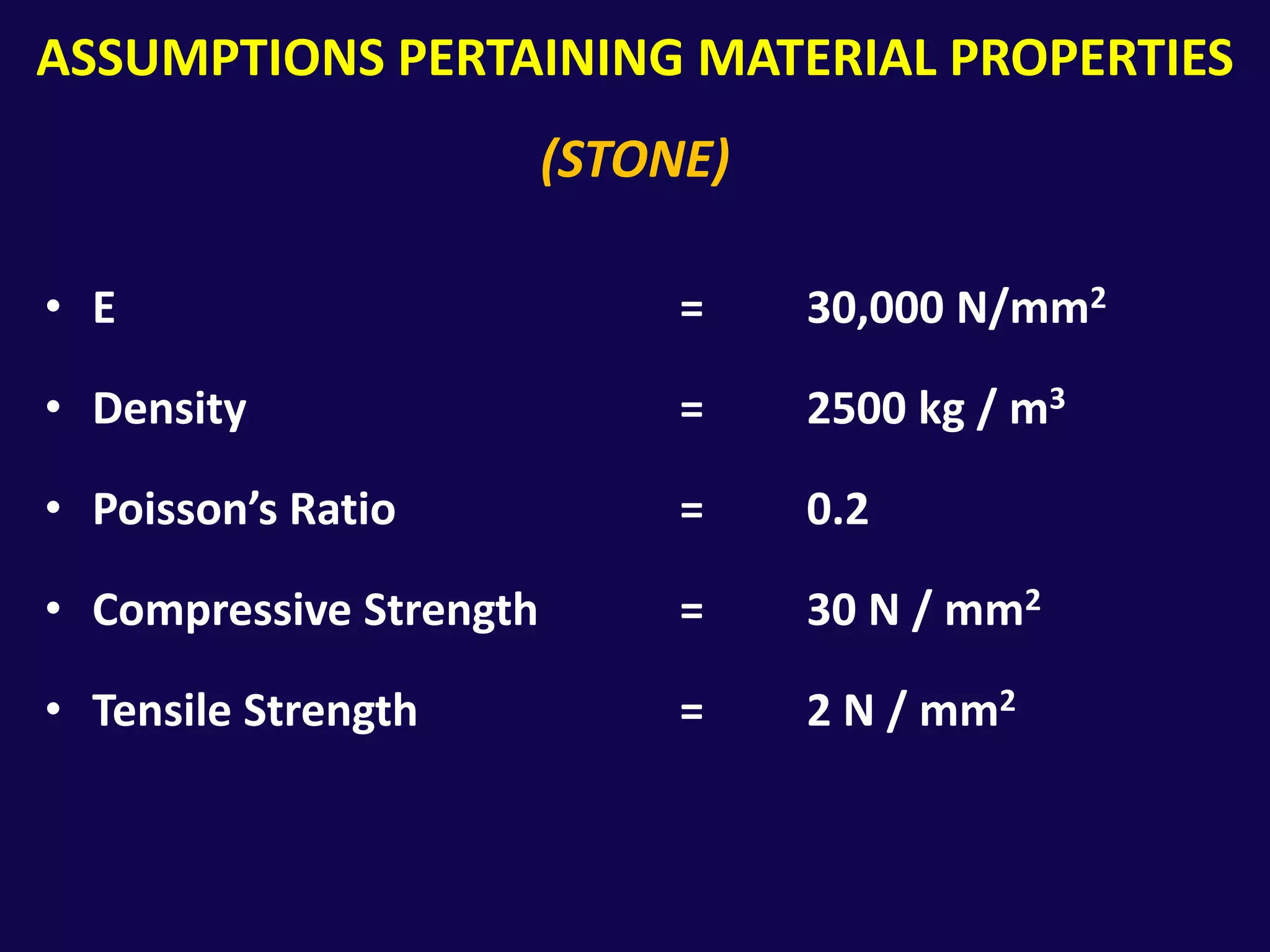
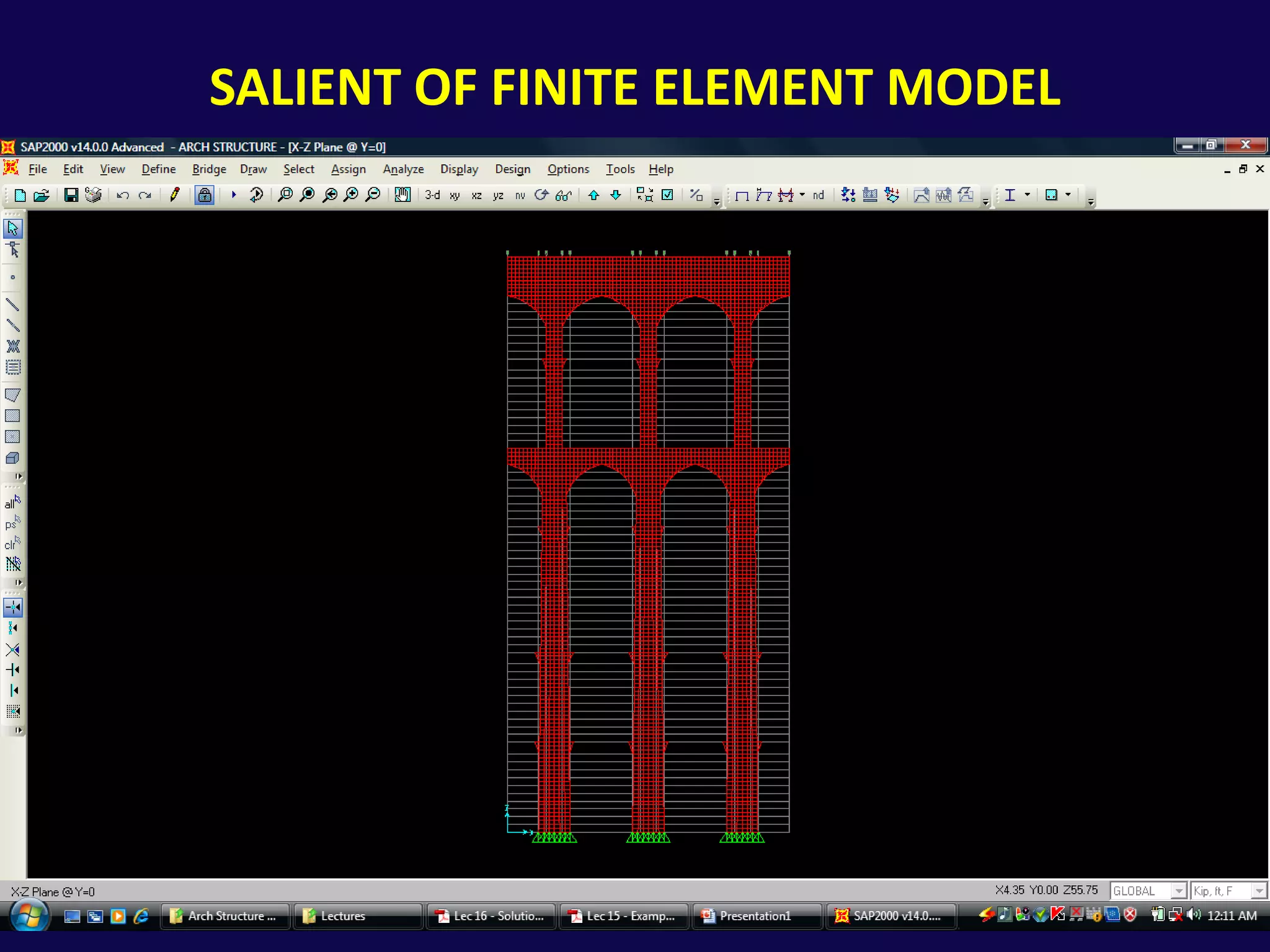
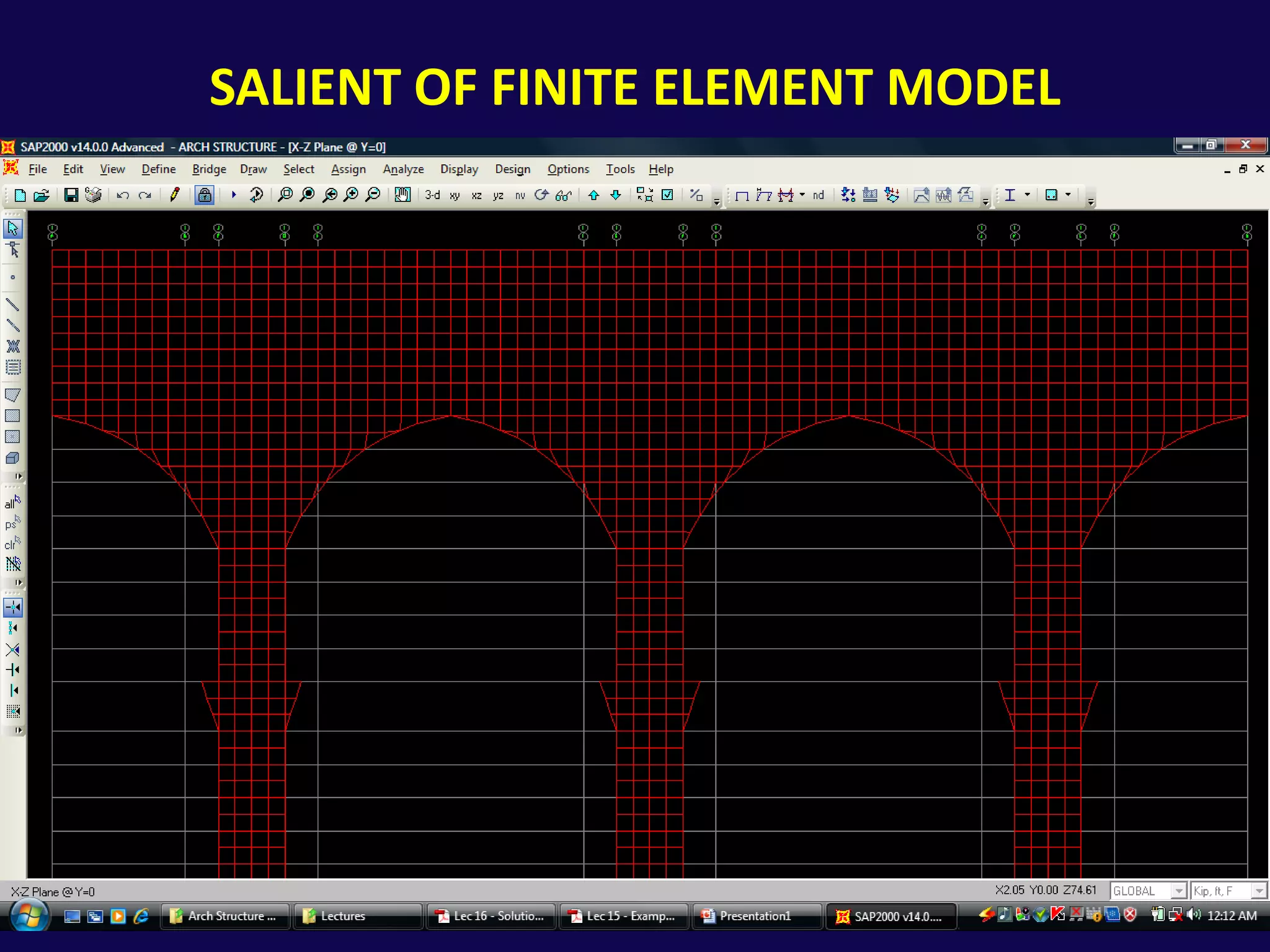
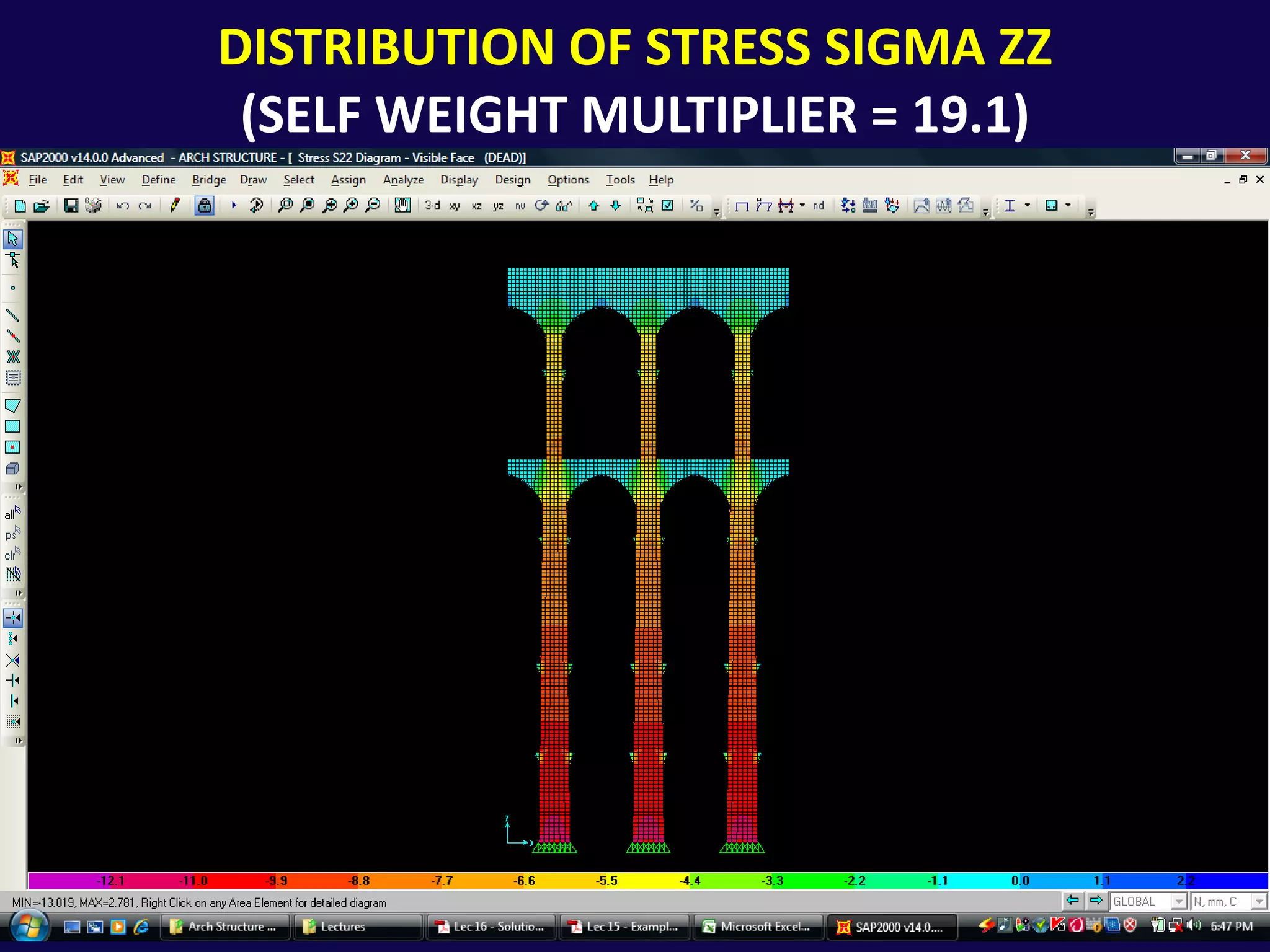
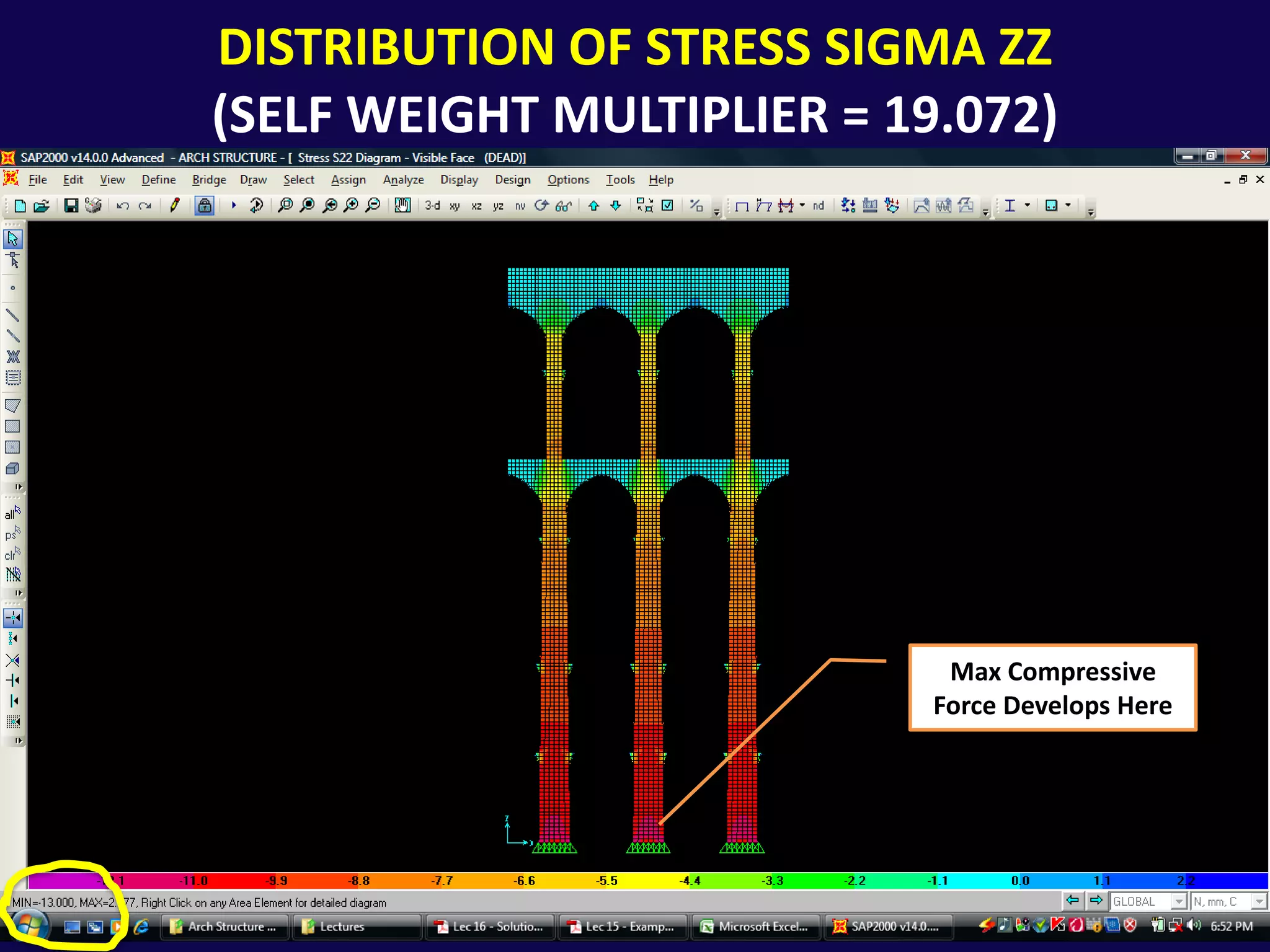
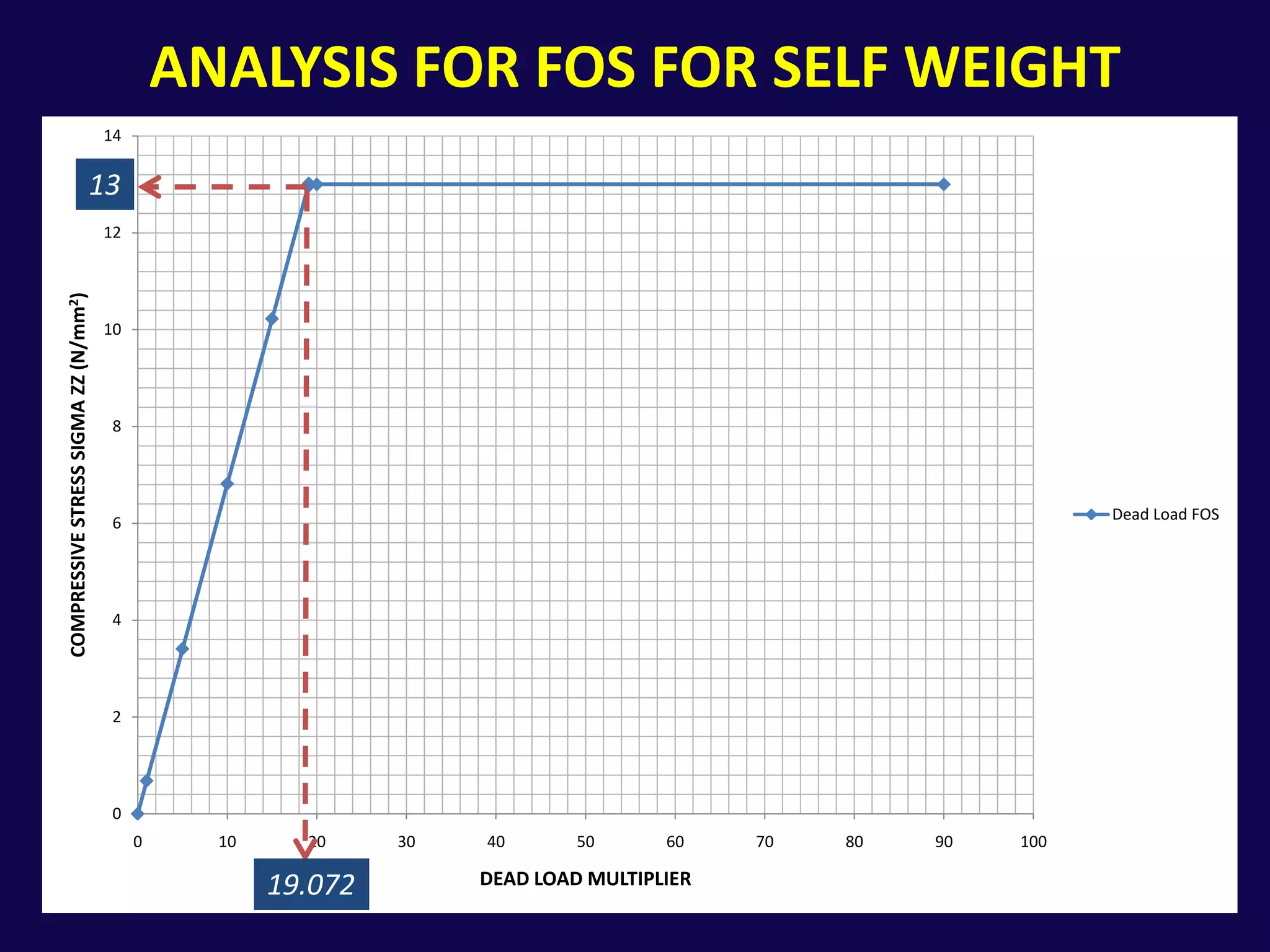
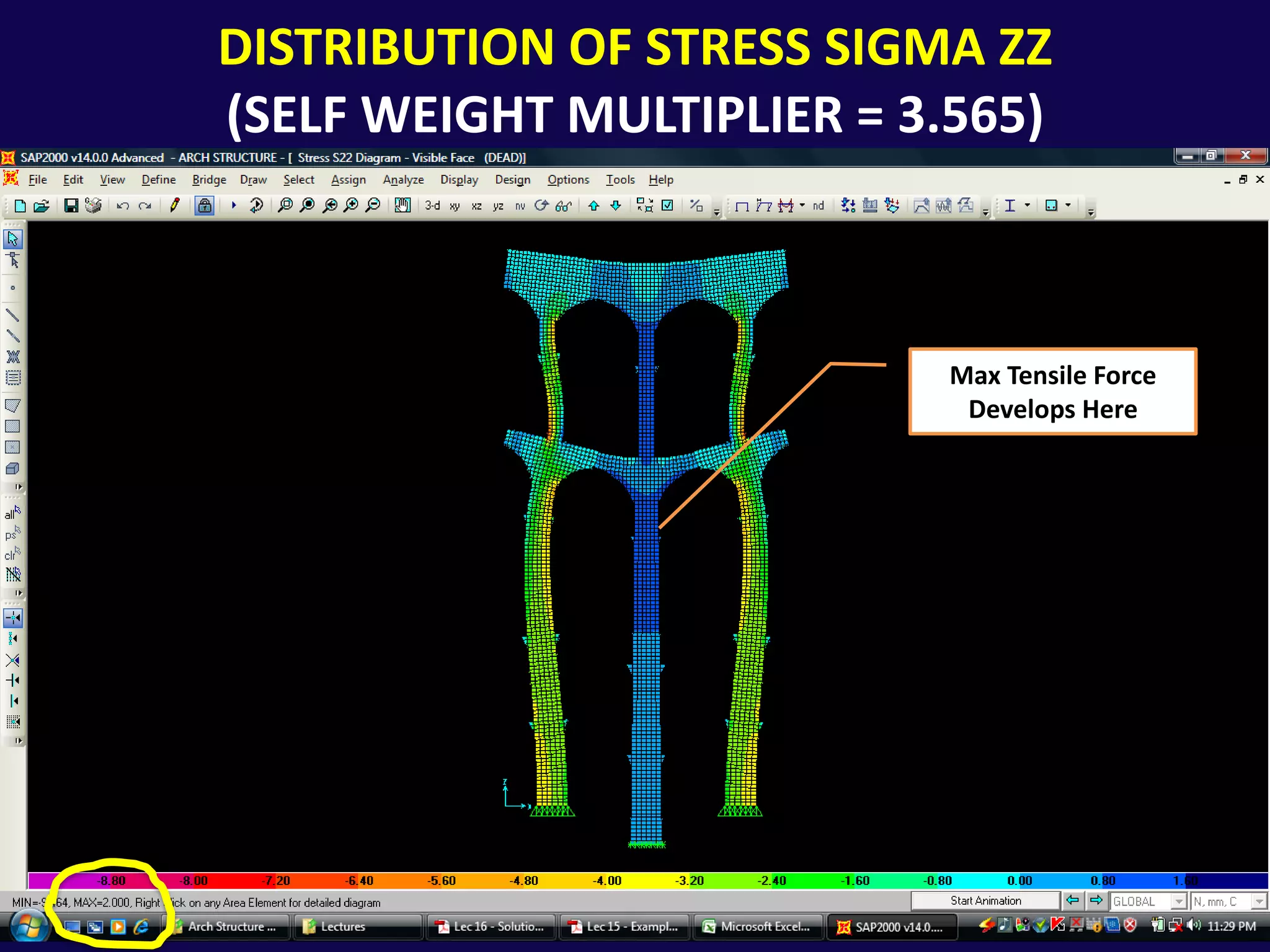
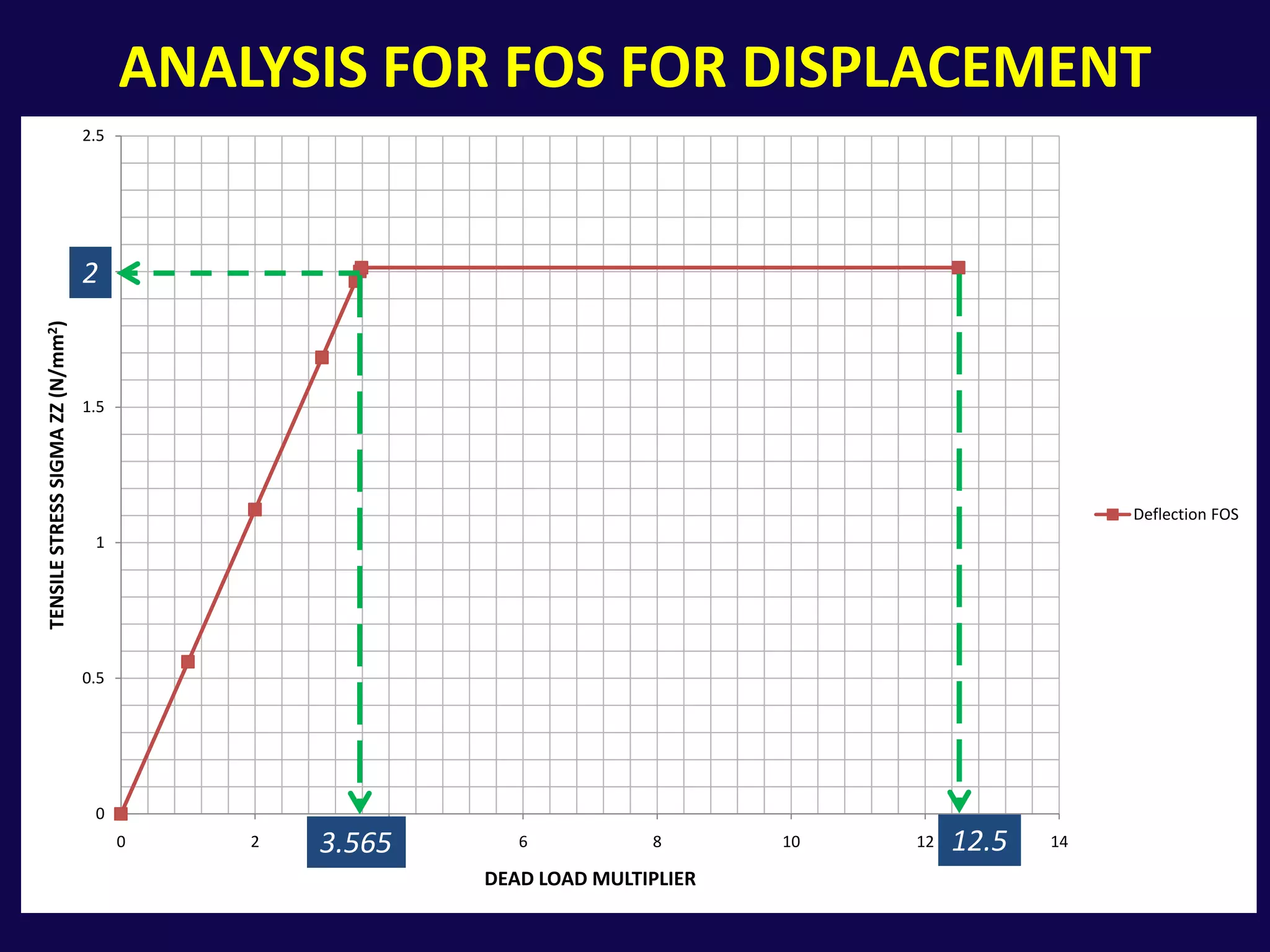
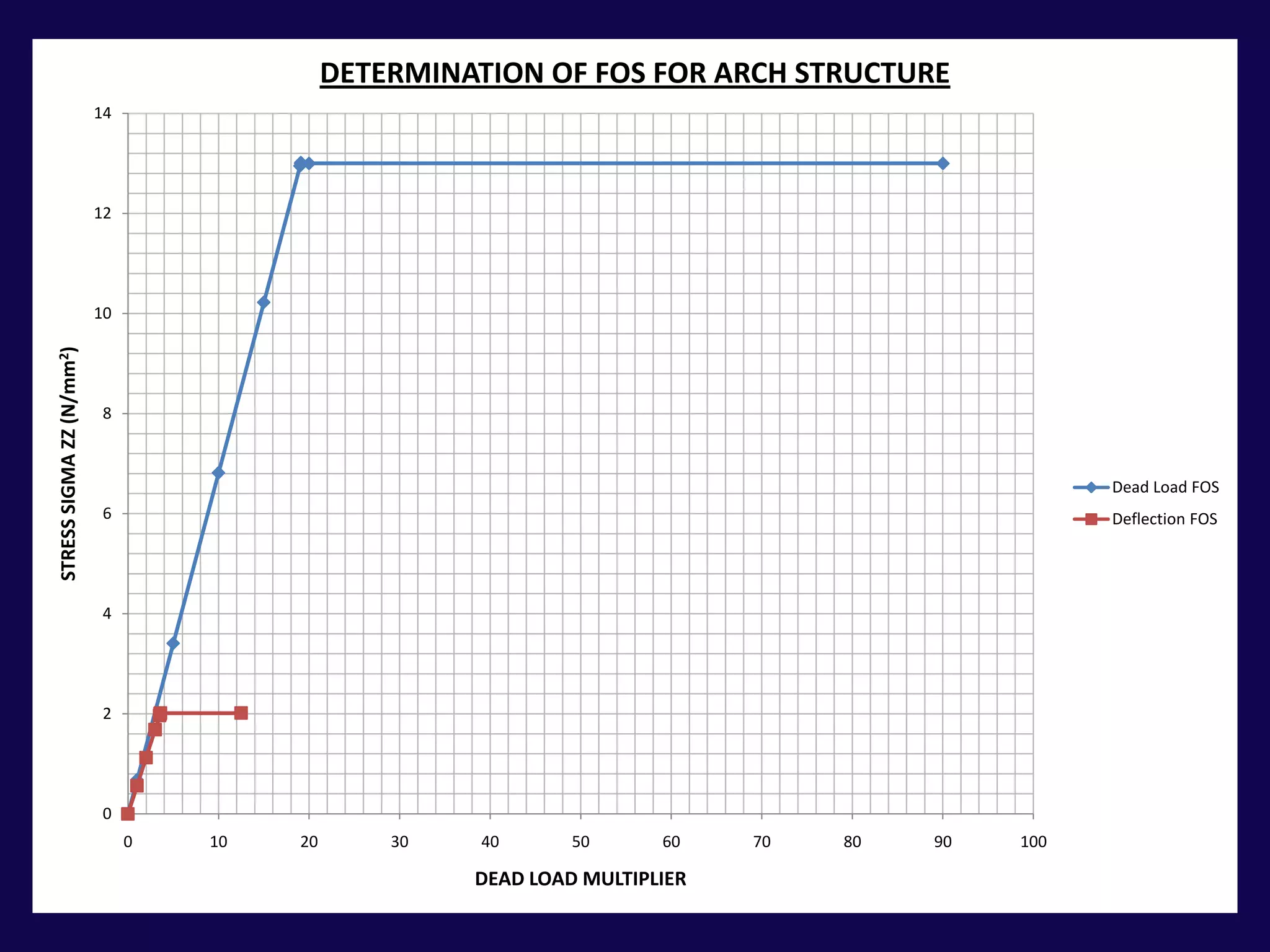
This document analyzes the structural safety of an arch structure using finite element modeling. It makes assumptions about the structure's geometry and the material properties of stone. A shell element model with 6-inch elements is used. Two analyses are performed: (1) for self-weight, the weight multiplier is incrementally increased until failure occurs at 19.072 times the actual weight; (2) for displacement, a boundary condition allows downward movement at the central pier, causing failure in tension at 3.565 times the displacement. The analyses determine safety factors for self-weight and displacement-induced failure modes.

1. ANALYSIS OF ARCH STRUCTURE

3. SEQUENCEAssumptions Pertaining Geometry of StructureAssumptions Pertaining Material PropertiesSalient of Finite Element ModelAnalysis for Factor of Safety for Self WeightAnalysis for Factor of Safety for DisplacementConclusion

4. Assumptions Pertaining Geometry of Structure5’8’1.5’2’ Thick10’2’8’3’ Thick1’73.5’15’1.5’10’1.5’10’4’ Thick

5. Assumptions Pertaining material properties(stone)E = 30,000 N/mm2Density = 2500 kg / m3Poisson’s Ratio = 0.2Compressive Strength = 30 N / mm2Tensile Strength = 2 N / mm2

6. Salient of finite element modelElement Type - Shell (Thick)Element Size - 6 inchesMaterial - Stone

7. Salient of finite element model

8. Salient of finite element model

9. Analysis for safety factor for self weight

10. PROCEDUREStart from self weight multiplier zeroIncrease the multiplier step by step and by iterative approach find the factor of safety required for collapseSince self weight acts downward causing compression in the structure so it will fail in compression

11. Distribution of stress sigma zz(Self weight multiplier = 0)

12. Distribution of stress sigma zz(Self weight multiplier = 1)

13. Distribution of stress sigma zz(Self weight multiplier = 5)

14. Distribution of stress sigma zz(Self weight multiplier = 10)

15. Distribution of stress sigma zz(Self weight multiplier = 15)

16. Distribution of stress sigma zz(Self weight multiplier = 19)

17. Distribution of stress sigma zz(Self weight multiplier = 20)

18. Distribution of stress sigma zz(Self weight multiplier = 19.1)

19. Distribution of stress sigma zz(Self weight multiplier = 19.072)Max Compressive Force Develops Here

20. Analysis for fos for self weight1319.072

21. Analysis for safety factor for displacement

22. PROCEDUREImpose boundary condition on central pier i.e allow downward movement so as to cause differential settlement in the structureStart from self weight multiplier zeroIncrease the multiplier step by step and by iterative approach find the factor of safety required for collapseSince differential settlement will cause tension in central pier so it will fail in tension

23. Distribution of stress sigma zz(Self weight multiplier = 0)

24. Distribution of stress sigma zz(Self weight multiplier = 1)

25. Distribution of stress sigma zz(Self weight multiplier = 2)

26. Distribution of stress sigma zz(Self weight multiplier = 3)

27. Distribution of stress sigma zz(Self weight multiplier = 3.5)

28. Distribution of stress sigma zz(Self weight multiplier = 3.59)

29. Distribution of stress sigma zz(Self weight multiplier = 3.565)Max Tensile Force Develops Here

30. Analysis for fos for DISPLACEMENT212.53.565

31. CONCLUSION

33. CONCLUSIONSELF WEIGHT - 19.072DISPLACEMENTSTART OF MECHANISM - 3.565FAILURE - 12.5