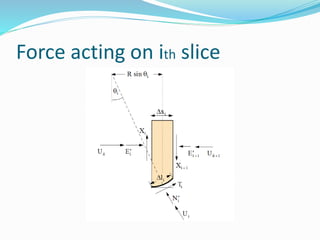
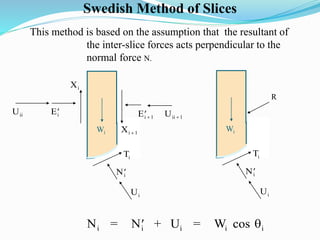
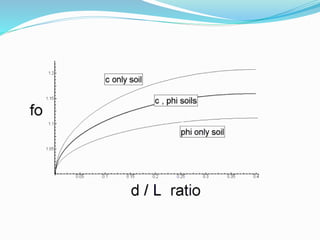
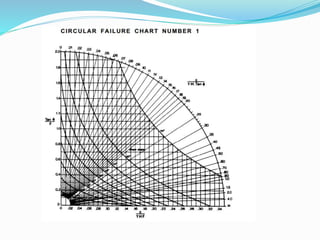
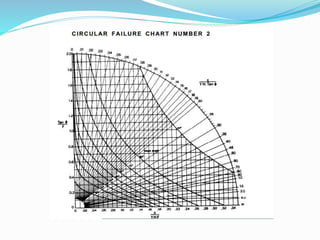
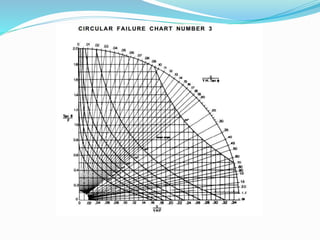
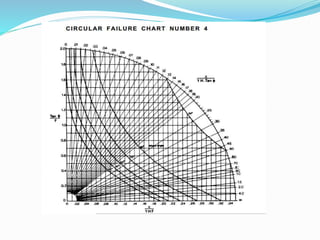
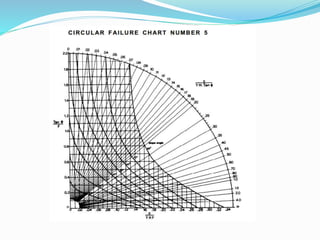
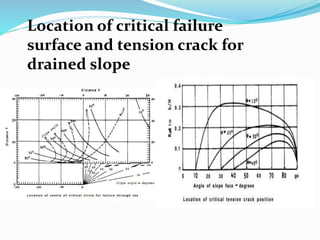
1. Rotational slope failures occur along a circular surface and theories are based on particles in rockmasses being small and not interlocked. 2. Stability charts are derived using assumptions like homogeneous material, shear strength equations, and failure surfaces passing through the slope toe. 3. Factor of safety is defined as the ratio of shear strength available to resist sliding to the shear stress required for equilibrium. Charts are used to locate failure surfaces and tension cracks for different groundwater conditions.

1. By
Charchit Jain

2. Condition for Rotational failure
 Failure is along the line of least resistance through the
slope , observation of various failure suggests that the
failure surface is generally takes the form of a circle
and most of the theories are based on this observation.
 The individual particles in the rockmass are very small
as compared with the size of the slope.
 These particles are not interlocked.

3. Derivation of Rotational failure
charts
 The following assumptions are made in deriving the
stability charts :
1. Material forming the slope is assumed to be
homogeneous.
2. τe = c + σ tan φ
3. Failure surface passes through the toe of the slope.
4. Location of the tension crack and the failure surface are
such that the FOS of the slope is minimum for the slope
geometry.
5. A range of ground water condition, from dry to fully
saturated condition are considered.

4.  Factor of safety of the slope is defined as =
and rearranging this equation, we obtain
τe = (c + σ tan φ)/FS
shear stress available to resist sliding depends upon the
distribution of normal stress (σ ) along this surface .
)surface(sliponmequilibriuforrequiredstressshear
)tan(cslidingresisttoavailablestrengthshear
e

FS

5.  Failure charts are produced depending upon the
ground water condition.
 Location of tension crack and the failure surface is
determined.

12. Example
 A 50 ft. high slope with the face angle of 40° is to be
excavated In the overburden soil with density ɗ = 100
lb/ft3 ,angle of friction is 30°, cohesive strength of c =
800 lb/ft2 , find the factor of safety of slope assuming it
to be a fully drained slope.
 value of (c/ɗ.H.tanØ) is 0.28 , so the corresponding
tanØ/F value for slope of 40° is 0.28 . Hence , the
Factor of safety is 2.061 .

13. Location of failure surface and
tension crack
 Charts are used for the construction of drawings of
potential slides.
 Charts are also used for the determination of location
of tension crack.
 Ground water condition is considered while selecting
the chart.

14. Location of critical failure
surface and tension crack for
drained slope

15. Location of critical failure surface
and tension crack in the presence
of ground water

16. Example
 A slope having face angle of 30° in a drained soil with
angle of friction is 20°. Locate the centre of critical
failure surface and tension crack .
 X = 0.2H
Y = 1.85H
b = 0.1H

17. Short term stability of soils with Ø = 0
 Failure will then occur along the circular arc of radius
R, and soil is assumed to be homogeneous.
F = Resisting moment / disturbing moment
Resisting moment = R2ØCu
Disturbing moment = Wx

18. Method of slicing
 For soil having Ø ≠ 0 , a more elaborate analysis is
required.
 Dividing the failure mass into number of slices,
preferably more than 5.

19. Force acting on ith slice

20. Overturning moment = R W
i=1
n
i i sin 
Restoring moment = R T
i=1
n
i
F
sisting Moment
Overturning Moment
c l N
W
i i i i
i
n
i i
i
n
 
   




Re
[ tan ]
sin
 

1
1
Case of drained slope is considered so Ui = 0

21. Swedish Method of Slices
This method is based on the assumption that the resultant of
the inter-slice forces acts perpendicular to the
normal force N.
Ei Ei 1
Uii Uii  1
Xi
Xi  1
Ti
Ni
Ui
Wi
Ti
Ni
Ui
Wi
R
N = N + U = Wi i i i i cos 

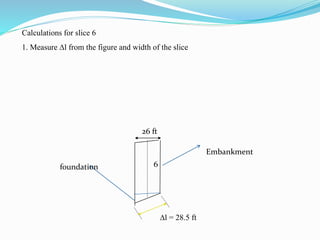
22. F =
[ c l + (W - U )
W
i=1
n
i i i i i i
i=1
n
i i


  cos tan ]
sin
 

F =
[ c l + W t
W
i=1
n
ui i i i ui
i=1
n
i i


 cos an ]
sin
 

For effective stress analysis
For total stress (undrained) analysis

23. Example

24. Calculations for slice 6
1. Measure l from the figure and width of the slice
6
26 ft
l = 28.5 ft
Embankment
foundation

25. Example
4. Determine the self-weight of the slice
6
26 ft
embankment
foundation
53.6ft
5 ft
W = A g = 257 pound/ft 3
10.4 ft

27.  Total resisting force = 640 kips
 Total driving force = 524 kips
Factor of safety = 640 / 524
= 1.22

28. Bishop’s simplified method
Assumption: The vertical inter-slice forces are equal and opposite. The resultant thus
acts perpendicular to W
Ei Ei 1
Uii Uii  1
Xi
Xi  1
Ti
Ni
Ui
Wi
Ti
Ni
Ui
Wi
R
W = T + N + u xi i i i i i isin cos  

29. W = T + N + u xi i i i i i isin cos  
T =
c l
F
+
N
F
i
i i i i   tan 








N =
W - u x - (1/ F) c x
1 +
F
i
i i i i i i
i
i i
  tan
cos
tan tan


 
now
hence

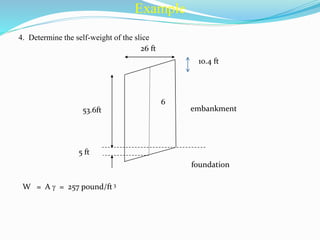
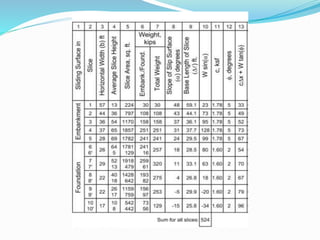
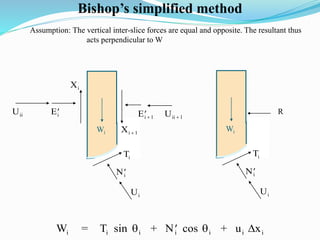
30. Substitution of the expression for N’ into the equation for the factor of safety
F
sisting Moment
Overturning Moment
c l N
W
i i i i
i
n
i i
i
n
 
   




Re
[ tan ]
sin
 

1
1
leads to
F =
( c x + ( W - u x ) )
1
M ( )
W
i=1
n
i i i i i i
i
i=1
n
i i


 





  tan
sin



where
M ( ) = [ 1 +
F
]i i i
i
  

cos tan
tan 

31. Janbu simplified method of slice
 It is based on the assumption that the failure surface
can be of general shape.
 Analysis of this method is similar to that of bishop’s
method.

33. The main methods for Rotational failure
analysis