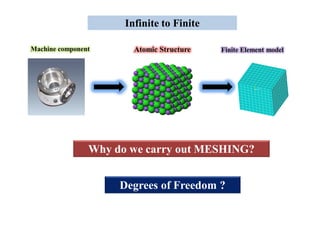
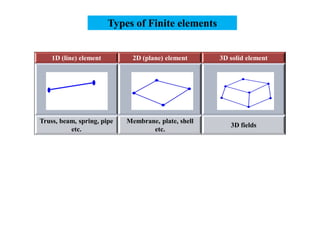
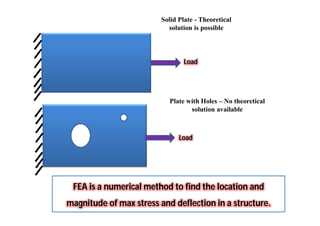
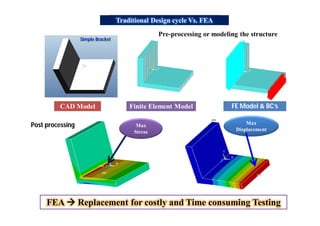
This document discusses finite element analysis (FEA) and its applications in engineering design. 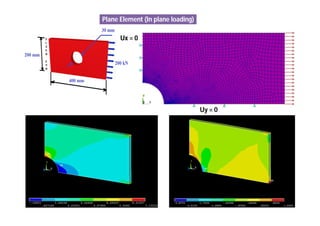It covers topics such as: - The different types of analyses that can be done, including 1D, 2D, and 3D analysis - The types of finite elements that can be used, such as beam, shell, and solid elements - How FEA can be used as a replacement for physical testing in the design process - Key steps in pre-processing and post-processing FEA models - Examples of how different elements model stresses, including axial, bending, torsional, and plane stresses

1. Dr.A.Vinoth Jebaraj, SMEC
VIT University, Vellore

2. DIFFERENT FAILURES OF MATERIALS?

3. So, On what basis we
have to design a machine
component?

4. Methods to solve any
Engineering problem
Experimental Analytical Numerical
Time consuming & needs
experimental setup
Atleast 3 to 5 prototypes must
be tested
Applicable only if physical
model is available
Approximate solution
Applicable if physical model is not
available
Real life complicated problems
100% accurate result
Applicable only for simple
problems
= y ?
Is this equation is correct
for the above beam?

5. Area = l × b
Area = ?
Error Solution

6. FEA is a numerical method to find the location and
magnitude of max stress and deflection in a structure.
Solid Plate - Theoretical
solution is possible
Plate with Holes – No theoretical
solution available
Load
Load

7. Challenge lies in representing the exact geometry of
the structure, especially, the curves.
Coarser
mesh
Fine
mesh
Regions where geometry is complex (curves,
notches, holes, etc.) require increased
number of elements to accurately represent
the shape.

8. Atomic Structure Finite Element model
Infinite to Finite
Degrees of Freedom ?
Why do we carry out MESHING?
Machine component

9. Types of Finite elements
1D (line) element 2D (plane) element 3D solid element
Truss, beam, spring, pipe
etc.
Membrane, plate, shell
etc.
3D fields

10. Traditional Design cycle Vs. FEA
FE Model & BC’sFinite Element ModelCAD Model
Max
Stress
Max
Displacement
Simple Bracket
FEA  Replacement for costly and Time consuming Testing
Pre-processing or modeling the structure
Post processing

11. Stresses vs. Resisting Area’s
(Fundamentals of stress analysis)
For Direct loading or Axial loading
For transverse loading
For tangential loading or twisting
Where I and J  Resistance properties of cross sectional area
I  Area moment of inertia of the cross section about the axes lying on the section
(i.e. xx and yy)
J  Polar moment of inertia about the axis perpendicular to the section

12. Plane of Bending
X – Plane
Y - Plane Z - Plane
Under what basis Ixx, Iyy and Izz
have to be selected in bending
equation?
Bending
Bending Twisting

13. Stress Tensor

14. Planar Assumptions
 All real world structures are three dimensional.
 For planar to be valid both the geometry and the loads must be constant across the thickness.
When using plane strain, we assume that the depth is infinite. Thus the effects from
end conditions may be ignored.

15. Plane Stress
 All stresses act on the one plane – normally the XY
plane.
 Due to Poisson effect there will be strain in the Z
direction. But We assume that there is no stress in
the Z – direction.
 σx, τxz, τyz will all be zero.
 All strains act on the one plane – normally the XY
plane. And hence there is no strain in the z-direction.
 σz will not equal to zero. Stress induced to prevent
displacement in z – direction.
 εx, εxz, εyz will all be zero.
Plane Strain

16.  A thin planar structure with constant thickness and loading within the plane of the
structure (xy plane).
 A long structure with uniform cross section and transverse loading along its length (z –
direction).

17. Stiffness
Axial stiffness = ; Bending stiffness = ; Torsional stiffness =

19. Types of Analysis
One dimensional
analysis
Two dimensional
analysis
Three dimensional
analysis
Uniaxial Loading Plane Loading Multiaxial Loading

20. Axial stressNodal displacement
FE Model Nodal displacement
Axially loaded Bar Element (Tension – Compression only)

21. Transverse loading Beam Element (Bending)
Nodal displacement
Bending stress
FE Model
Why I – section
is better?

22. Beam Element (Torsion)
Shear stress
Shear stress
11.02 MPa
11.3 MPa

23. 89.9 MPa

24. Plane Element (In plane loading)
Uy = 0
Ux = 0

25. Shell Element (plate bending)
“Membrane forces + bending moment”
Example: car body and tank containers

26. Quadratic Element Vs. Triangular Element
Quadratic element is more
accurate than triangular
element (due to better
interpolation function)
Tria element is stiffer than quad,
results in lesser stress and
displacement if used in critical
locations.