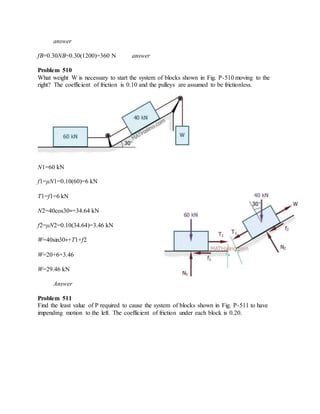
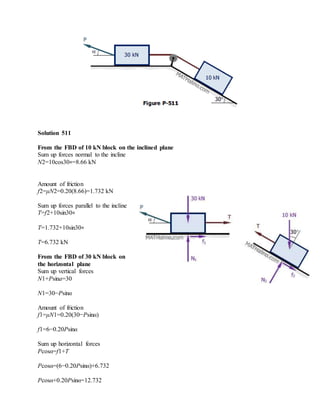
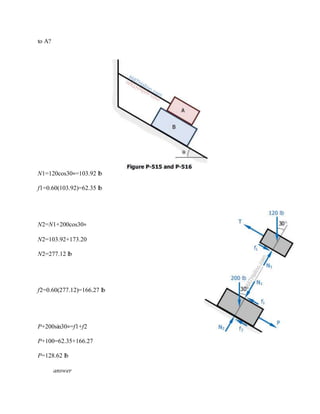
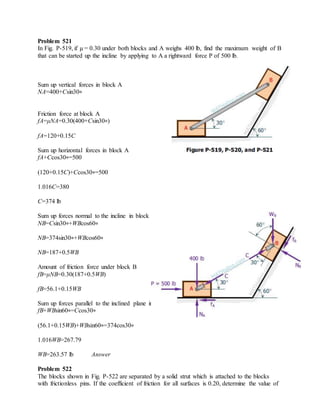
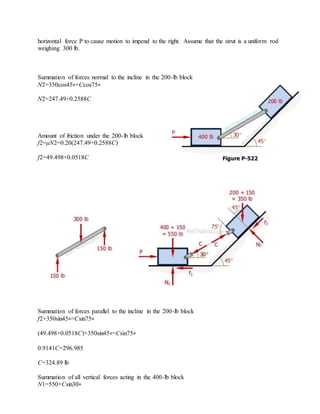
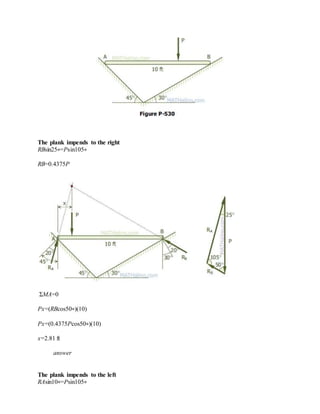
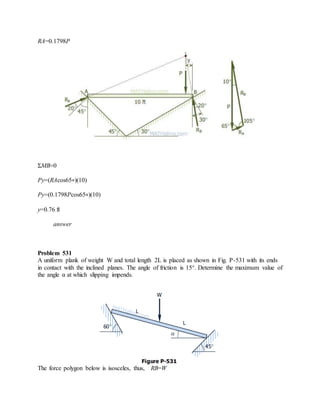
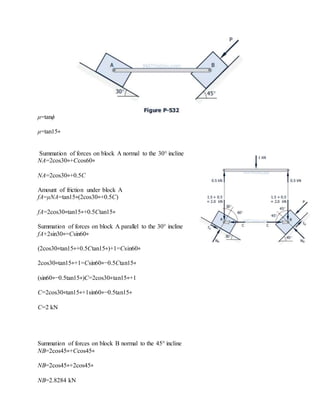
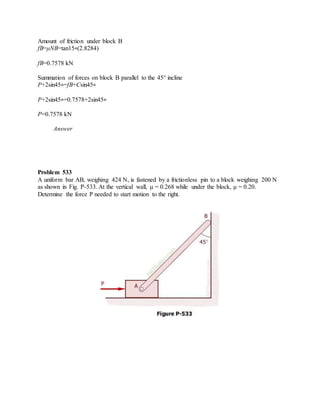
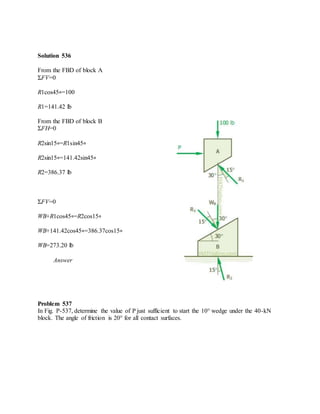
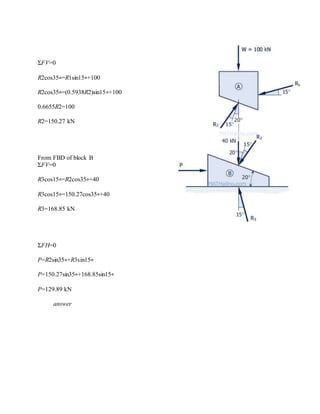
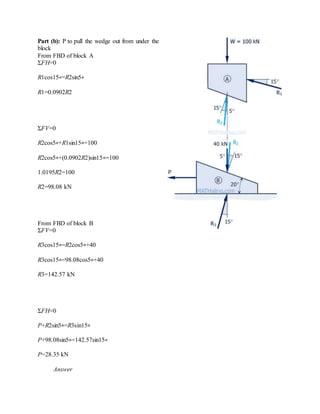
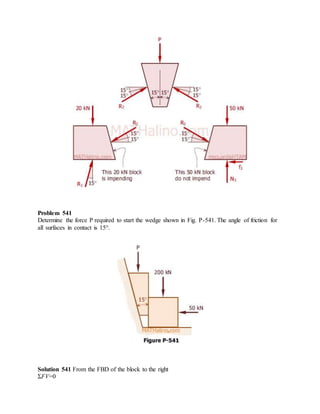
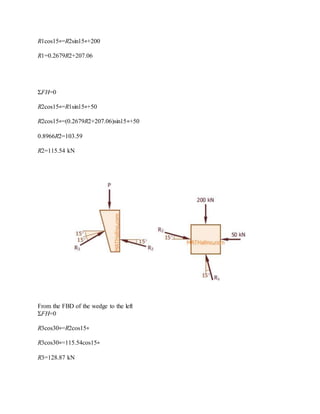
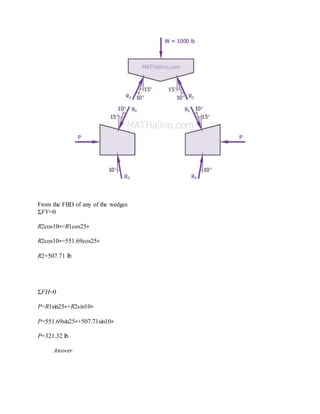
The blocks and ladder problems can be summarized as follows: 1) The documents provide diagrams of blocks on inclined planes or ladders against walls, connected by cords or as single structures. 2) Frictional forces are calculated using coefficients of friction for each surface. 3) Force and moment sums are used to relate normal and frictional forces to weights, angles, and applied forces to determine minimum/maximum values for motion to occur.

1. The blocks shown in Fig. P-509 are connected by flexible, inextensible cords passing over
frictionless pulleys. At A the coefficients of friction are μs = 0.30 and μk = 0.20 while at B they
are μs = 0.40 and μk = 0.30. Compute the magnitude and direction of the friction force acting on
each block.
Neglecting friction
TA=3000sinθ=3000(3/5)
TA=1800 N
TB=2000sinα=2000(4/5)
TB=1600 N
2TA is greater than TB, thus, the system will move to the left if contact surfaces are frictionless.
Considering friction
The angle of static friction at A, ɸA = arctan 0.30 = 16.70°, is not enough to hold the block from
sliding the incline of angle θ = arctan (3/4) = 36.87° from horizontal.
If TB is insufficient to hold 2TA statically the system will move to the left, otherwise, the system
is stationary.
Assume the blocks are stationary (use μs)
NA=3000cosθ=3000(45)=2400 N
fA=0.30NA=0.30(2400)=720 N
TA=3000sinθ−fA=3000(35)−720=1080 N
2TA=2160 N
NB=2000cosα=2000(35)=1200 N
fB=0.40NB=0.40(1200)=480 N
TB=2000sinα+fB=2000(45)+480=2080 N
TB < 2TA. TB is insufficient to hold the system in static equilibrium, thus, the blocks are moving
to the left.
Blocks are moving to the left (Use μk)
fA=0.20NA=0.20(2400)=480 N

2. answer
fB=0.30NB=0.30(1200)=360 N answer
Problem 510
What weight W is necessary to start the system of blocks shown in Fig. P-510 moving to the
right? The coefficient of friction is 0.10 and the pulleys are assumed to be frictionless.
N1=60 kN
f1=μN1=0.10(60)=6 kN
T1=f1=6 kN
N2=40cos30∘=34.64 kN
f2=μN2=0.10(34.64)=3.46 kN
W=40sin30∘+T1+f2
W=20+6+3.46
W=29.46 kN
Answer
Problem 511
Find the least value of P required to cause the system of blocks shown in Fig. P-511 to have
impending motion to the left. The coefficient of friction under each block is 0.20.

3. Solution 511
From the FBD of 10 kN block on the inclined plane
Sum up forces normal to the incline
N2=10cos30∘=8.66 kN
Amount of friction
f2=μN2=0.20(8.66)=1.732 kN
Sum up forces parallel to the incline
T=f2+10sin30∘
T=1.732+10sin30∘
T=6.732 kN
From the FBD of 30 kN block on
the horizontal plane
Sum up vertical forces
N1+Psina=30
N1=30−Psinα
Amount of friction
f1=μN1=0.20(30−Psinα)
f1=6−0.20Psinα
Sum up horizontal forces
Pcosα=f1+T
Pcosα=(6−0.20Psinα)+6.732
Pcosα+0.20Psinα=12.732

4. P(cosα+0.20sinα)=12.732
P=12.732cosα+0.20sinα
To minimize P, differentiate then equate to zero
dPdα=−12.732(−sinα+0.20cosα)(cosα+0.20sinα)2=0
−sinα+0.20cosα=0
sinα=0.20cosα
tanα=0.20
α=11.31∘
Thus,
Pmin=12.732cos11.31∘+0.20sin11.31∘
Pmin=12.5 kN
Answer
Problem 512
A homogeneous block of weight W rests upon the incline shown in Fig. P-512. If the coefficient
of friction is 0.30, determine the greatest height h at which a force P parallel to the incline may
be applied so that the block will slide up the incline without tipping over.
Sliding up the incline
ΣFy=0
N=Wcosθ=45W
f=μN=0.30(45W)=625W

5. ΣFx=0
P=Wsinθ+f
P=35W+625W
P=2125W
Tipping over
ΣMA=0
Ph=40(Wsinθ)+20(Wcosθ)
2125Wh=40(35W)+20(45W)
h=47.62 cm
answer
Problem 513
In Fig. P-512, the homogeneous block weighs 300 kg and the coefficient of friction is 0.45. If h
= 50 cm, determine the force P to cause motion to impend.

6. ΣFy=0
N=300cosθ=300(45)
N=240 kg
f=μN=0.45(240)
f=108 kg
ΣFx=0
P+f=300sinθ
P+108=300(35)
P=72 kg
Answer
Problem 514
The 10-kN cylinder shown in Fig. P-514 is held at rest on the 30° incline by a weight P
suspended from a cord wrapped around the cylinder. If slipping impends, determine P and the
coefficient of friction.

7. Solution 514
a=10cos60∘=5 cm
b=10−a=5 cm
ΣMA=0
Pb=Wcyla
P(5)=10(5)
P=10 kN answer
ΣMO=0
10f=10P
f=P
f=10 kN
ΣFy=0
N=10cos30∘+Pcos30∘
N=10cos30∘+10cos30∘
N=17.32 kN
f=μN
10=μ(17.32)
μ=0.577
answer

8. Problem 515
Block A in Fig. P-515 weighs 120 lb, block B weighs 200 lb, and the cord is parallel to the
incline. If the coefficient of friction for all surfaces in contact is 0.25, determine the angle θ of
the incline of which motion of B impends.
N1=120cosθ
f1=0.25(120cosθ)=30cosθ
N2=N1+200cosθ
N2=120cosθ+200cosθ
N2=320cosθ
f2=0.25(320cosθ)=80cosθ
f1+f2=200sinθ
30cosθ+80cosθ=200sinθ
110cosθ=200sinθ
100200=sinθcosθ
tanθ=1120
θ=28.81∘
answer
Problem 516
Referring to Fig. P-515 if the coefficient of friction is 0.60 and θ = 30°, what force P applied to B
acting down and parallel to the incline will start motion? What is the tension in the cord attached

9. to A?
N1=120cos30∘=103.92 lb
f1=0.60(103.92)=62.35 lb
N2=N1+200cos30∘
N2=103.92+173.20
N2=277.12 lb
f2=0.60(277.12)=166.27 lb
P+200sin30∘=f1+f2
P+100=62.35+166.27
P=128.62 lb
answer

10. T=f1+120sin30∘
T=62.35+60
T=122.35 lb
Answer
Problem 519
In Fig. P-519, two blocks are connected by a solid strut attached to each block with frictionless
pins. If the coefficient of friction under each block is 0.25 and B weighs 2700 N, find the
minimum weight of A to prevent motion.
Solution 519
Sum up forces normal to the incline in block B
NB=2700cos60∘+Csin30∘
NB=1350+0.5C
Amount of friction for impending motion of block B
fB=μNB=0.25(1350+0.5C)
fB=337.5+0.125C
Sum up all forces parallel to the incline in block B
fB+Ccos30∘=2700sin60∘
(337.5+0.125C)+Ccos30∘=2700sin60∘
0.991C=2000.77
C=2018.89 N

11. Summation of vertical forces acting on block A
NA=WA+Csin30∘
NA=WA+2018.89sin30∘
NA=WA+1009.44
Amount of friction under block A at impending motion
fA=μNA=0.25(WA+1009.44)
fA=0.25WA+252.36
Summation of horizontal forces on block A
fA=Ccos30∘
0.25WA+252.36=2018.89cos30∘
WA=5984.20 N
Answer
Problem 520
Referring to Fig. P-519, block A weighs 4 kN and B weighs 3 kN. If μ = 0.20 under B, compute
the minimum coefficient of friction under A to prevent motion.
Summation of forces perpendicular to the inclined plane in block B
NB=30cos60∘+Csin30∘
NB=15+0.5C

12. Amount of friction in block B at impending motion
fB=μBNB=0.20(15+0.5C)
fB=3+0.10C
fB+Ccos30∘=3sin60∘
(3+0.10C)+Ccos30∘=30sin60∘
0.966C=22.98
C=23.79 kN
Summation of vertical forces in block A
NA=40+Csin30∘
NA=40+23.79sin30∘
NA=51.895 kN
Summation of horizontal forces in block A
fA=Ccos30∘
fA=23.79cos30∘
fA=20.60 kN
Coefficient of friction at A
fA=μANA
20.60=μA(51.895)
μA=0.397
answer

13. Problem 521
In Fig. P-519, if μ = 0.30 under both blocks and A weighs 400 lb, find the maximum weight of B
that can be started up the incline by applying to A a rightward force P of 500 lb.
Sum up vertical forces in block A
NA=400+Csin30∘
Friction force at block A
fA=μNA=0.30(400+Csin30∘)
fA=120+0.15C
Sum up horizontal forces in block A
fA+Ccos30∘=500
(120+0.15C)+Ccos30∘=500
1.016C=380
C=374 lb
Sum up forces normal to the incline in block B
NB=Csin30∘+WBcos60∘
NB=374sin30∘+WBcos60∘
NB=187+0.5WB
Amount of friction force under block B
fB=μNB=0.30(187+0.5WB)
fB=56.1+0.15WB
Sum up forces parallel to the inclined plane in block B
fB+WBsin60∘=Ccos30∘
(56.1+0.15WB)+WBsin60∘=374cos30∘
1.016WB=267.79
WB=263.57 lb Answer
Problem 522
The blocks shown in Fig. P-522 are separated by a solid strut which is attached to the blocks
with frictionless pins. If the coefficient of friction for all surfaces is 0.20, determine the value of

14. horizontal force P to cause motion to impend to the right. Assume that the strut is a uniform rod
weighing 300 lb.
Summation of forces normal to the incline in the 200-lb block
N2=350cos45∘+Ccos75∘
N2=247.49+0.2588C
Amount of friction under the 200-lb block
f2=μN2=0.20(247.49+0.2588C)
f2=49.498+0.0518C
Summation of forces parallel to the incline in the 200-lb block
f2+350sin45∘=Csin75∘
(49.498+0.0518C)+350sin45∘=Csin75∘
0.9141C=296.985
C=324.89 lb
Summation of all vertical forces acting in the 400-lb block
N1=550+Csin30∘

15. N1=550+324.89sin30∘
N1=712.45 lb
Amount of friction under the 400-lb block
f1=μN1=0.20(712.45)
f1=142.50 lb
Solving for the required P by summing up horizontal forces in the 400-lb block
P=f1+Ccos30∘
P=142.50+324.89cos30∘
P=423.85 lb
Answer
Problem 523
A force of 400 lb is applied to the pulley shown in Fig. P-523. The pulley is prevented from
rotating by a force P applied to the end of the brake lever. If the coefficient of friction at the
brake surface is 0.20, determine the value of P.
ΣMO=0
20f=10(400)
f=200 lb
f=μN
200=0.20N
N=1000 lb

16. ΣMA=0
48P+8f=16N
48P+8(200)=16(1000)
48P=14400
P=300 lb
answer
Problem 524
A horizontal arm having a bushing of 20 mm long is slipped over a 20-mm diameter vertical rod,
as shown in Fig. P-524. The coefficient of friction between the bushing and the rod is 0.20.
Compute the minimum length L at which a weight W can be placed to prevent the arm from
slipping down the rod. Neglect the weight of the arm.
Solution 524
ΣMO=0
10N=WL

17. N=0.10WL
Note:
the sum of Δf will pass through point O, thus, f has no moment effect at O.
Amount of friction force
f=μN=0.20(0.10WL)
f=0.02WL
ΣFV=0
f=W
0.02WL=W
L=50 mm
Answer
Problem 525
A uniform ladder 4.8 m ft long and weighing W lb is placed with one end on the ground and the
other against a vertical wall. The angle of friction at all contact surfaces is 20°. Find the
minimum value of the angle θ at which the ladder can be inclined with the horizontal before
slipping occurs.

18. Coefficient of friction
μ=tanϕ=tan20∘
μ=0.364
Friction forces at each end of the ladder
fA=μNA=0.364NA
fB=μNB=0.364NB
ΣFH=0
NB=fA
NB=0.364NA
ΣFV=0
NA+fB=W
NA+0.364NB=W
NA+0.364(0.364NA)=W
1.1325NA=W
NA=0.883W
Thus,
fA=0.364(0.883W)
fA=0.3214W
ΣMB=0
W(2.4cosθ)+fA(4.8sinθ)=NA(4.8cosθ)
Wcosθ+2fAsinθ=2NAcosθ
W+2fAtanθ=2NA
W+2(0.3214W)tanθ=2(0.883W)
1+0.6428tanθ=1.766
0.6428tanθ=0.766
tanθ=1.191 661 481

19. θ=50∘
answer
Problem 526
A ladder 6 m long has a mass of 18 kg and its center of gravity is 2.4 m from the bottom. The
ladder is placed against a vertical wall so that it makes an angle of 60° with the ground. How far
up the ladder can a 72-kg man climb before the ladder is on the verge of slipping? The angle of
friction at all contact surfaces is 15°.
Solution 526
Coefficient of friction
μ=tanϕ
μ=tan15∘
Amount of friction at contact surfaces
fA=μNA=NAtan15∘
fB=μNB=NBtan15∘
ΣFV=0
NA+fB=18+72
NA=90−fB
NA=90−NBtan15∘
ΣFH=0
fA=NB
NAtan15∘=NB
(90−NBtan15∘)tan15∘=NB
90tan15∘−NBtan215∘=NB
90tan15∘=NB+NBtan215∘

20. NB(1+tan215∘)=90tan15∘
NB=90tan15∘1+tan215∘
NB=22.5 kg
fB=22.5tan15∘
fB=6.03 kg
ΣMA=0
NB(6sin60∘)+fB(6cos60∘)=18(2.4cos60∘)+72(xcos60∘)
NB(6tan60∘)+6fB=18(2.4)+72x
6(22.5)tan60∘+6(6.03)=43.2+72x
72x=226.81
x=3.15 m
answer
Problem 527
A homogeneous cylinder 3 m in diameter and weighing 30 kN is resting on two inclined planes
as shown in Fig. P-527. If the angle of friction is 15° for all contact surfaces, compute the
magnitude of the couple required to start the cylinder rotating counterclockwise.

21. ΣFH=0
NAcos15∘=NBcos75∘
NA=0.2679NB
ΣFV=0
NAsin15∘+NBsin75∘=30
(0.2679NB)sin15∘+NBsin75∘=30
1.0353NB=30
NB=28.98 kN
NA=0.2679(28.98)
NA=7.76 kN
μ=tan15∘=0.2679
fA=μNA=0.2679(7.76)
fA=2.08 kN
fB=μNB=0.2679(28.98)
fB=7.76 kN
Required couple
C=ΣMcenter
C=1.5(fA+fB)=1.5(2.08+7.76)
C=14.76 kN⋅m
Answer

22. Problem 528
Instead of a couple, determine the minimum horizontal force P applied tangentially to the left at
the top of the cylinder described in Prob. 527 to start the cylinder rotating counterclockwise.
1.5F=1.5fA+1.5fB
F=fA+fB
F=2.08+7.76
F=9.84 kN
Answer
Problem 529
As shown in Fig. P-529, a homogeneous cylinder 2 m in diameter and weighing 12 kN is acted
upon by a vertical force P. Determine the magnitude of P necessary to start the cylinder turning.
Assume that μ = 0.30.
When the cylinder starts to turn due to P, the normal force under horizontal surface is zero. See
the free body diagram below.

23. x=(1)(sin60∘)
x=123√ m
ΣMA=0
(1+x)P=12x
(1+123√)P=12(123√)
1.866P=10.392
P=5.569 kN
Answer
Problem 530
A plank 10 ft long is placed in a horizontal position with its ends resting on two inclined planes,
as shown in Fig. P-530. The angle of friction is 20°. Determine how close the load P can be
placed to each end before slipping impends.

24. The plank impends to the right
RBsin25∘=Psin105∘
RB=0.4375P
ΣMA=0
Px=(RBcos50∘)(10)
Px=(0.4375Pcos50∘)(10)
x=2.81 ft
answer
The plank impends to the left
RAsin10∘=Psin105∘

25. RA=0.1798P
ΣMB=0
Py=(RAcos65∘)(10)
Py=(0.1798Pcos65∘)(10)
y=0.76 ft
answer
Problem 531
A uniform plank of weight W and total length 2L is placed as shown in Fig. P-531 with its ends
in contact with the inclined planes. The angle of friction is 15°. Determine the maximum value of
the angle α at which slipping impends.
The force polygon below is isosceles, thus, RB=W

26. ΣMA=0
(RBcos30∘)(2Lcosα)=W(Lcosα)+(RBsin30∘)(2Lsinα)
(Wcos30∘)(2Lcosα)=W(Lcosα)+(Wsin30∘)(2Lsinα)
2WLcos30∘cosα=WLcosα+2WLsin30∘sinα
2cos30∘cosα=cosα+2sin30∘sinα
2cos30∘cosα−cosα=2sin30∘sinα
(2cos30∘−1)cosα=2sin30∘sinα
2cos30∘−12sin30∘=sinαcosα
tanα=3√−1
α=arctan(3√−1)
α=36.21∘ answer
Problem 532
In Fig. P-532, two blocks each weighing 1.5 kN are connected by a uniform horizontal bar which
weighs 1.0 kN. If the angle of friction is 15° under each block, find P directed parallel to the 45°
incline that will cause impending motion to the left.

27. μ=tanϕ
μ=tan15∘
Summation of forces on block A normal to the 30° incline
NA=2cos30∘+Ccos60∘
NA=2cos30∘+0.5C
Amount of friction under block A
fA=μNA=tan15∘(2cos30∘+0.5C)
fA=2cos30∘tan15∘+0.5Ctan15∘
Summation of forces on block A parallel to the 30° incline
fA+2sin30∘=Csin60∘
(2cos30∘tan15∘+0.5Ctan15∘)+1=Csin60∘
2cos30∘tan15∘+1=Csin60∘−0.5Ctan15∘
(sin60∘−0.5tan15∘)C=2cos30∘tan15∘+1
C=2cos30∘tan15∘+1sin60∘−0.5tan15∘
C=2 kN
Summation of forces on block B normal to the 45° incline
NB=2cos45∘+Ccos45∘
NB=2cos45∘+2cos45∘
NB=2.8284 kN

28. Amount of friction under block B
fB=μNB=tan15∘(2.8284)
fB=0.7578 kN
Summation of forces on block B parallel to the 45° incline
P+2sin45∘=fB+Csin45∘
P+2sin45∘=0.7578+2sin45∘
P=0.7578 kN
Answer
Problem 533
A uniform bar AB, weighing 424 N, is fastened by a frictionless pin to a block weighing 200 N
as shown in Fig. P-533. At the vertical wall, μ = 0.268 while under the block, μ = 0.20.
Determine the force P needed to start motion to the right.

29. Solution 533
ΣMA=0
NB(2x)=424x+fB(2x)
2NB=424+2fB
2NB=424+2(0.268NB)
1.464NB=424
NB=289.62 N
fB=0.268(289.62)
fB=77.62 N
ΣFV=0
NA=fB+200+424
NA=77.62+200+424
NA=701.62 N
fA=0.20(701.62)
fA=140.32 N
ΣFH=0
P=fA+NB
P=140.32+289.62
P=429.94 N
Answer
Problem 535
A wedge is used to split logs. If φ is the angle of friction between the wedge and the log,
determine the maximum angle a of the wedge so that it will remain embedded in the log.

30. Solution 535
ΣFH=0
P=2Rsin(ϕ+12α)
∂P∂α=12Rcos(ϕ+12α)=0
cos(ϕ+12α)=0
ϕ+12α=90∘
2ϕ+α=180∘
α=180∘−2ϕ
sinα=sin(180∘−2ϕ)
sinα=sin180∘cos2ϕ−cos180∘sin2ϕ
sinα=(0)(cos2ϕ)−(−1)(sin2ϕ)
sinα=sin2ϕ
α=2ϕ
answer
Problem 536
in Fig. P-536, determine the minimum weight of block B that will keep it at rest while a force P
starts blocks A up the incline surface of B. The weight of A is 100 lb and the angle of friction for
all surfaces in contact is 15°.

31. Solution 536
From the FBD of block A
ΣFV=0
R1cos45∘=100
R1=141.42 lb
From the FBD of block B
ΣFH=0
R2sin15∘=R1sin45∘
R2sin15∘=141.42sin45∘
R2=386.37 lb
ΣFV=0
WB+R1cos45∘=R2cos15∘
WB+141.42cos45∘=386.37cos15∘
WB=273.20 lb
Answer
Problem 537
In Fig. P-537, determine the value of P just sufficient to start the 10° wedge under the 40-kN
block. The angle of friction is 20° for all contact surfaces.

32. From the FBD of 40 kN block
ΣFH=0
R1sin80∘=R2sin30∘
R1=R2sin30∘sin80∘
R1=0.5077R2
ΣFV=0
R2cos30∘+R1cos80∘=40
R2cos30∘+(0.5077R2)cos80∘=40
0.9542R2=40
R2=41.92 kN
From the FBD of lower block
ΣFV=0
R3cos20∘=R2cos30∘
R3cos20∘=41.92cos30∘
R3=38.634 kN
ΣFH=0
P=R2sin30∘+R3sin20∘
P=41.92sin30∘+38.634sin20∘
P=34.174 kN
Answer

33. Problem 538
In Problem 537, determine the value of P acting to the left that is required to pull the wedge out
from under the 40-kN block.
Solution 538
From the FBD of 40 kN block
ΣFH=0
R1cos20circ=R2sin10∘
R1=R2sin10∘cos20∘
R1=0.1848R2
ΣFV=0
R1sin20∘+R2cos10∘=40
(0.1848R2)sin20∘+R2cos10∘=40
1.048R2=40
R2=38.168 kN
From the FBD of lower block
ΣFV=0
R3cos20∘=R2cos10∘

34. R3cos20∘=38.168cos10∘
R3=40 kN
ΣFH=0
P=R2sin10∘+R3sin20∘
P=38.168sin10∘+40sin20∘
P=20.308 kN
Answer
Problem 539
The block A in Fig. P-539 supports a load W = 100 kN and is to be raised by forcing the wedge
B under it. The angle of friction for all surfaces in contact is f = 15°. If the wedge had a weight
of 40 kN, what value of P would be required (a) to start the wedge under the block and (b) to pull
the wedge out from under the block?
Part (a): P to start the wedge under block A
From the FBD of block A
ΣFH=0
R1cos15∘=R2sin35∘
R1=0.5938R2

35. ΣFV=0
R2cos35∘=R1sin15∘+100
R2cos35∘=(0.5938R2)sin15∘+100
0.6655R2=100
R2=150.27 kN
From FBD of block B
ΣFV=0
R3cos15∘=R2cos35∘+40
R3cos15∘=150.27cos35∘+40
R3=168.85 kN
ΣFH=0
P=R2sin35∘+R3sin15∘
P=150.27sin35∘+168.85sin15∘
P=129.89 kN
answer

36. Part (b): P to pull the wedge out from under the
block
From FBD of block A
ΣFH=0
R1cos15∘=R2sin5∘
R1=0.0902R2
ΣFV=0
R2cos5∘+R1sin15∘=100
R2cos5∘+(0.0902R2)sin15∘=100
1.0195R2=100
R2=98.08 kN
From FBD of block B
ΣFV=0
R3cos15∘=R2cos5∘+40
R3cos15∘=98.08cos5∘+40
R3=142.57 kN
ΣFH=0
P+R2sin5∘=R3sin15∘
P+98.08sin5∘=142.57sin15∘
P=28.35 kN
Answer

37. Problem 540
As shown in Fig. P-540, two blocks each weighing 20 kN and resting on a horizontal surface, are
to be pushed apart by a 30° wedge. The angle of friction is 15° for all contact surfaces. What
value of P is required to start movement of the blocks? How would this answer be changed if the
weight of one of the blocks were increased by 30 kN?
Solution 540
From the FBD of 20-kN block
ΣFH=0
R1sin15∘=R2cos30∘
R1=3.346R2
ΣFV=0
R1cos15∘=R2sin30∘+20
(3.346R2)cos15∘=R2sin30∘+20
2.732R2=20
R2=7.32 kN

38. From the FBD of the upper block
ΣFV=0
P=2R2sin30∘
P=2(7.32)sin30∘
P=7.32 kN
answer
When one block weigh 50 kN and the other is 20 kN, the first to impend when movement starts
is the 20 kN block. Thus the reaction R2 = 7.32 kN, similar to the above value of R2. Thus, the
answer which is P = 7.32 kN will not change. See the free body diagram below and note that the
friction reaction f3 is not equal to the maximum available friction under the 50 kN block.

39. Problem 541
Determine the force P required to start the wedge shown in Fig. P-541. The angle of friction for
all surfaces in contact is 15°.
Solution 541 From the FBD of the block to the right
ΣFV=0

40. R1cos15∘=R2sin15∘+200
R1=0.2679R2+207.06
ΣFH=0
R2cos15∘=R1sin15∘+50
R2cos15∘=(0.2679R2+207.06)sin15∘+50
0.8966R2=103.59
R2=115.54 kN
From the FBD of the wedge to the left
ΣFH=0
R3cos30∘=R2cos15∘
R3cos30∘=115.54cos15∘
R3=128.87 kN

41. ΣFV=0
P=R2sin15∘+R3sin30∘
P=115.54sin15∘+128.87sin30∘
P=94.34 kN
Answer
Problem 542
What force P must be applied to the wedges shown in Fig. P-542 to start them under the block?
The angle of friction for all contact surfaces is 10°.
Solution 542
From the FBD of 1000 lb block
ΣFV=0
2(R1cos25∘)=1000
R1=551.69 lb

42. From the FBD of any of the wedges
ΣFV=0
R2cos10∘=R1cos25∘
R2cos10∘=551.69cos25∘
R2=507.71 lb
ΣFH=0
P=R1sin25∘+R2sin10∘
P=551.69sin25∘+507.71sin10∘
P=321.32 lb
Answer

43. Problem 543
To adjust the vertical position of a column supporting 200-kN load, two 5° wedges are used as
shown in Fig. P-543. Determine the force P necessary to start the wedges is the angle of friction
at all contact surfaces is 25°. Neglect friction at the rollers.
From the FBD of the upper wedge
ΣFV=0
R2cos30∘=200
R2=230.94 kN
From the FBD of the lower wedge
ΣFV=0
R3cos25∘=R2cos30∘
R3cos25∘=230.94cos30∘
R3=220.68 kN
ΣFH=0
P=R2sin30∘+R3sin25∘

44. P=230.94sin30∘+220.68sin25∘
P=208.73 kN
answer