This document discusses different types of pendulums, including their definitions, components, and equations. It begins by defining a simple pendulum as a weight suspended from a pivot that swings freely due to gravity. It then lists various pendulum types: simple, compound, Kater's, Foucault, and torsional. For each type, it provides details on components and equations for period and acceleration due to gravity. The key equations shown are the period equation T=2π√(L/g) for a simple pendulum and T=2π(I/mgh)^1/2 for the period of a compound pendulum, where I is the moment of inertia.

2. WHAT IS PENDULUM ?
• Is a WEIGHT suspended from a PIVOT
so it can SWING freely.
• When displaced it is subjected to a
restoring force due to gravity which allows
it to accelerate it back and forth.
• Kinetic v/s Potential
• The time for one complete cycle, a left
swing and a right swing is called the
PERIOD.

3. TYPES OF PENDULUM
SIMPLE PENDULUM COMPOUND
PENDULUM KATER’S PENDULUM
FOUCAULT PENDULUM
TORSIONAL PENDULUM

4. SIMPLE PENDULUM
•A simple pendulum is one which can be considered to be a point mass suspended
from a string or rod of negligible mass. It is a resonant system with a single
resonant frequency.
•A simple pendulum has a small-diameter bob and a string that has a very small
mass but is strong enough not to stretch appreciably.
•A simple pendulum is defined to have an object that has a small mass, also
known as the pendulum bob, which is suspended from a light wire or string.
•Exploring the simple pendulum a bit further, we can discover the conditions under
which it performs simple harmonic motion, and we can derive an interesting
expression for its period.

5. For the simple pendulum :
The period of a pendulum is the time it
takes the pendulum to make one full
back-and-forth swing.
PERIOD OF SIMPLE
PENDULUM…

6. EQUATIONS
OF SIMPLE
PENDULUM
If the pendulum weight or bob of a simple pendulum is
pulled to a relatively small angle and let go, it will swing
back and forth at a regular frequency. If damping effects
from air resistance and friction are negligible, equations
concerning the frequency and period of the pendulum, as
well as the length of the string can be calculated.
The period
equation is:
T = 2π√(L/g)
The frequency
equation is:
f = [√(g/L)]/2π
The length
equations are:
L = g/(4π2f2)
and
L = gT2/4π2

7. COMPOUND PENDULUM
 Any swinging rigid body free to rotate about a
fixed horizontal axis is called a compound
pendulum or physical pendulum.
 The appropriate equivalent length for calculating
the period of any such pendulum is the distance
from the pivot to the center of oscillation.
 Exploring the compound pendulum a bit further,
we can discover the conditions under which it
performs Simple Harmonic motion, and we can
derive an interesting expression for its period.

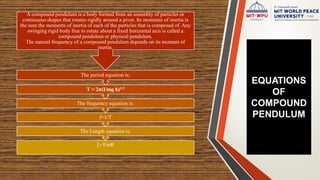
8. PERIOD OF COMPOUND
PENDULUM
The period of a
pendulum is the time it
takes the pendulum to
make one full back-
and-forth swing.
For Compound
Pendulum :
T = 2π(I/mgh)1/2 T = 2π([k2 + h2]/gh)1/2
Where “I” is Moment of Inertia

9. EQUATIONS
OF
COMPOUND
PENDULUM
L=I/mR
The Length equation is:
f=1/T
The frequency equation is:
T = 2π(I/mg h)1/2
The period equation is:
A compound pendulum is a body formed from an assembly of particles or
continuous shapes that rotates rigidly around a pivot. Its moments of inertia is
the sum the moments of inertia of each of the particles that is composed of. Any
swinging rigid body free to rotate about a fixed horizontal axis is called a
compound pendulum or physical pendulum.
The natural frequency of a compound pendulum depends on its moment of
inertia.

10. KATER’S PENDULUM
• A Kater's pendulum is a reversible free swinging pendulum invented
by British physicist and army captain Henry Kater in 1817 for use as
a gravimeter instrument to measure the local acceleration of gravity.
• Its advantage is that, unlike previous pendulum gravimeters, the
pendulum's center of gravity and center of oscillation do not have to be
determined, allowing greater accuracy.
• The Kater's pendulum consists of a rigid metal bar with two pivot
points, one near each end of the bar. It can be suspended from either
pivot and swung.
• It also has either an adjustable weight that can be moved up and
down the bar, or one adjustable pivot, to adjust the periods of swing.

11. PERIOD OF KATER’S
PENDULUM
• A pendulum can be used to measure the acceleration of
gravity g because for narrow swings its period of
swing T depends only on g and its length L.
• So by measuring the length L and period T of a
pendulum, g can be calculated.
• Repeatedly timing each period of a Kater pendulum, and
adjusting the weights until they were equal, was time
consuming and error-prone. Friedrich Bessel showed in 1826
that this was unnecessary. As long as the periods measured
from each pivot, T1 and T2, are close in value, the period T of
the equivalent simple pendulum can be calculated from
them:
• T^2= T1^2+T2^2/2+T1^2-T2^2/2(h1+h2/h1-h2)

12. ACCELERATION
DUE TO GRAVITY
BY KATER’S
PENDULUM
•The Kater's pendulum consists of a rigid metal bar with two
pivot points, one near each end of the bar. It can be
suspended from either pivot and swung. It also has either an
adjustable weight that can be moved up and down the bar, or
one adjustable pivot, to adjust the periods of swing.
• In use, it is swung from one pivot, and the period timed,
and then turned upside down and swung from the other
pivot, and the period timed. The movable weight (or pivot)
is adjusted until the two periods are equal. At this point the
period T is equal to the period of an 'ideal' simple pendulum
of length equal to the distance between the pivots. From the
period and the measured distance L between the pivots, the
acceleration of gravity can be calculated with great
precision.
•The acceleration due to gravity by Kater's pendulum is
given by:

13. TORSIONAL PENDULUM
•A Torsional Pendulum consists of a disk (or
some other object) suspended from a wire,
which is then twisted and released, resulting in
an oscillatory motion.
•The oscillatory motion is caused by a
restoring torque which is proportional to the
angular displacement.
•Similar to the simple pendulum, so long as
the angular displacement is small (which
means the motion is SHM) the period is
independent of the displacement.
•Torsional pendulums are also used as a time
keeping devices, as in for example, the
mechanical wristwatch.

14. PERIOD OF TORSIONAL
PENDULUM
I is the rotational inertia of the disk about
the twisting axis, k (kappa) is the torsional
constant (equivalent to the spring
constant). This equation is exactly the
same as SHM we have already discussed.
By direct comparison the period of the
torsional pendulum is given by,

15. EQUATION OF RESTORING TORQUE OF TORSIONAL
PENDULUM
The oscillatory motion is caused by a restoring torque which is proportional to
the angular displacement.

16. THANK YOU…