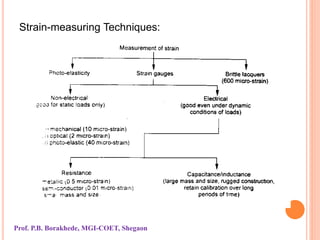
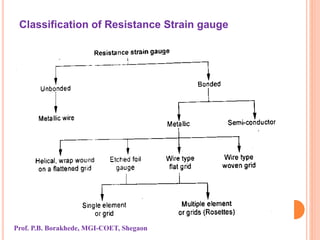
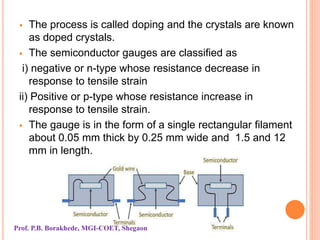
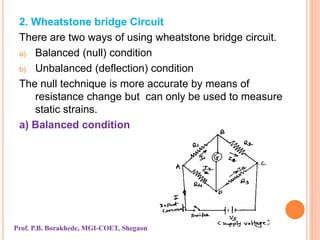
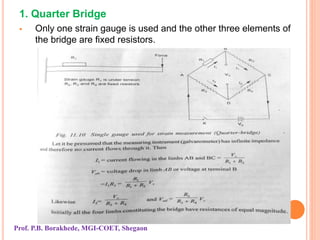
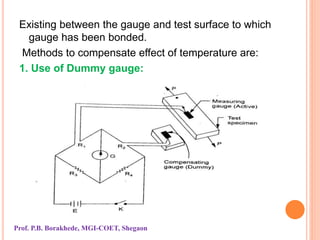
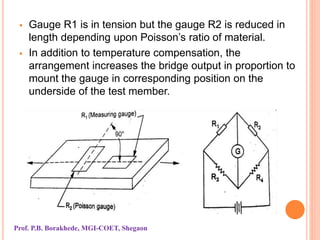
The document covers the principles and applications of strain gauges and pressure measurement devices, detailing types (bonded and unbonded gauges), their circuit configurations (balancing, Wheatstone bridge), and temperature compensation methods. It emphasizes the importance of strain measurement in engineering to ensure safety and effectiveness in designs by accurately measuring stress and related forces. Additionally, it outlines the designs of different strain gauges, their operational principles, and requirements for effective measurements under varying conditions.