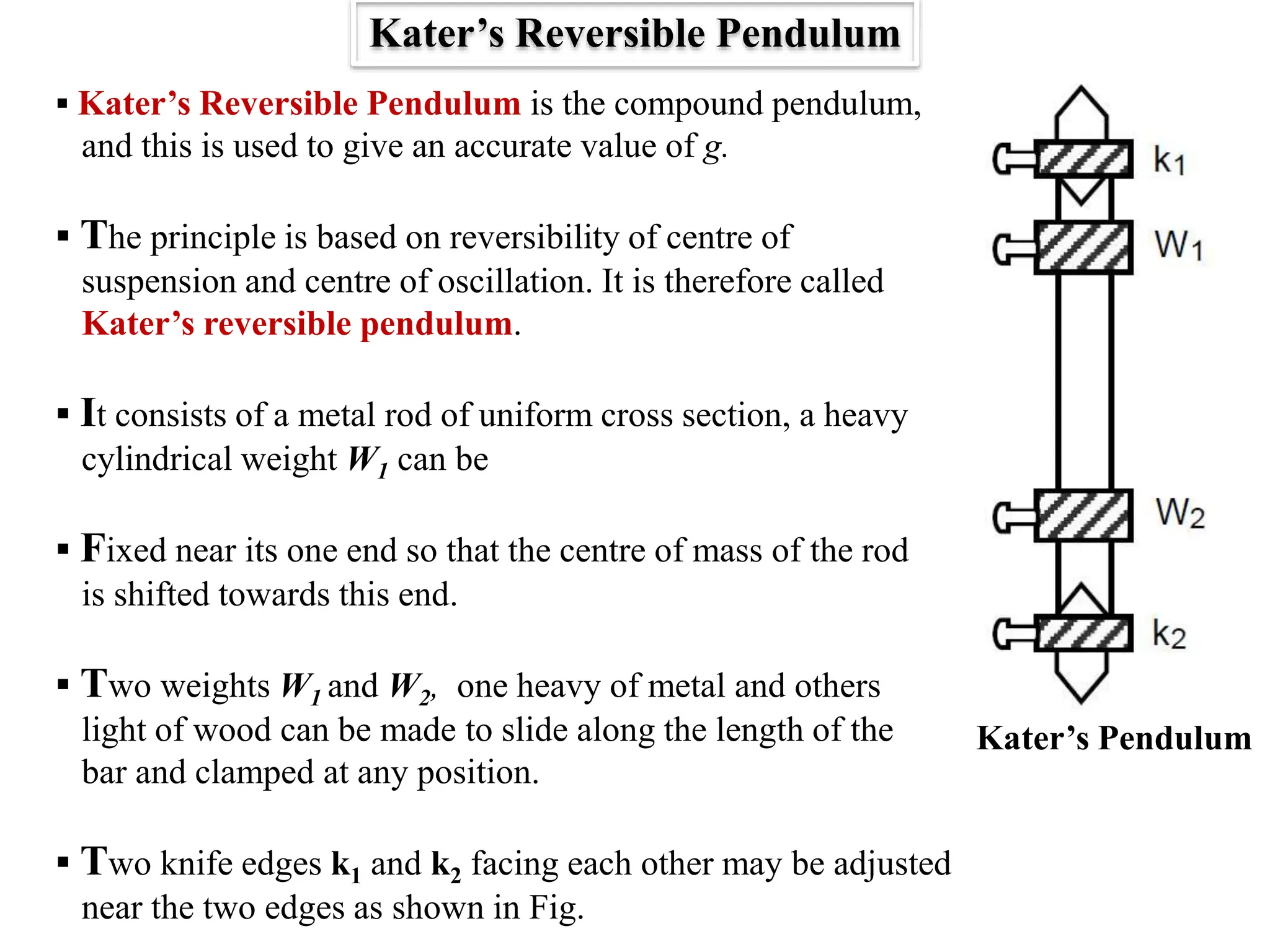
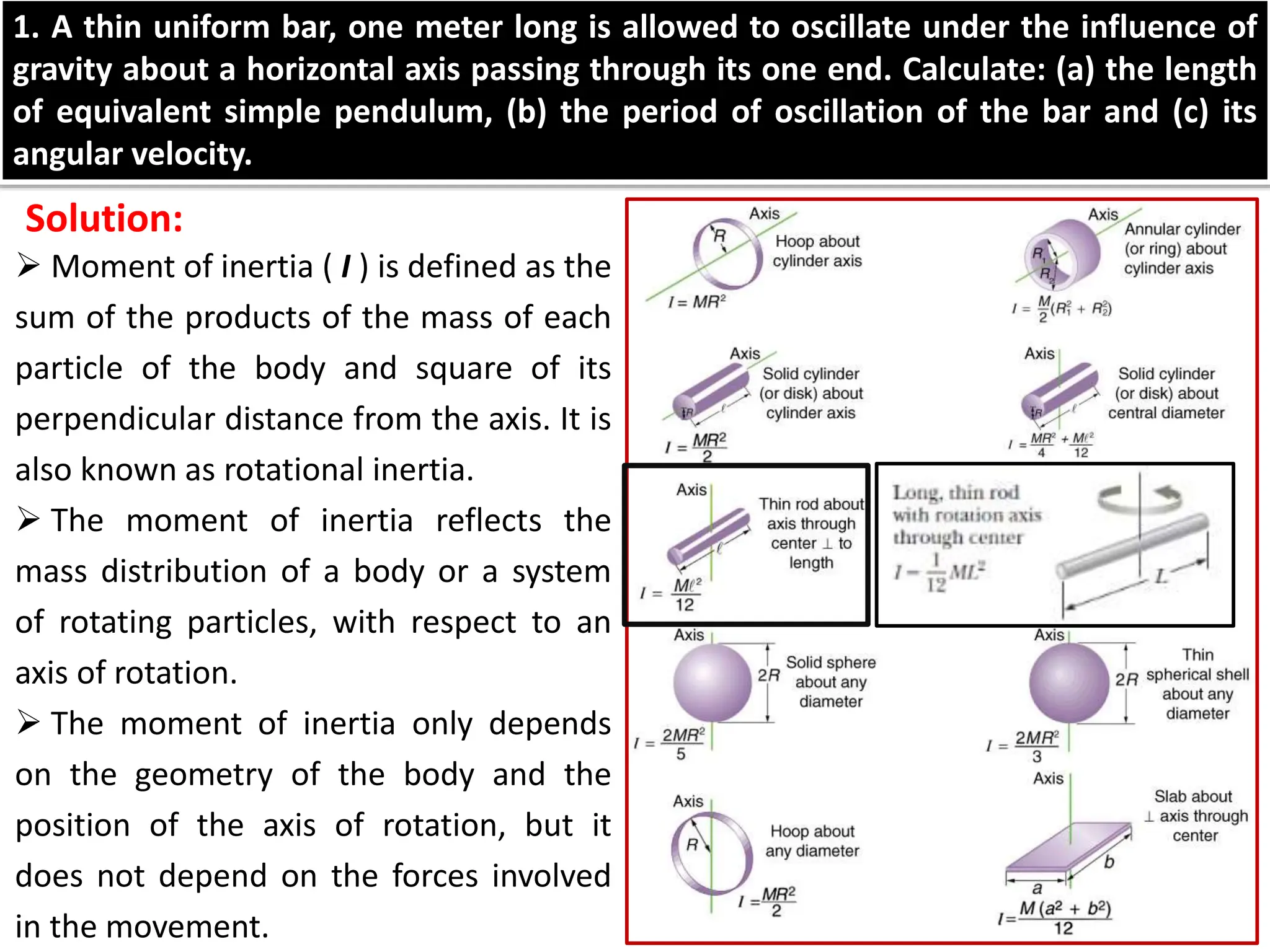
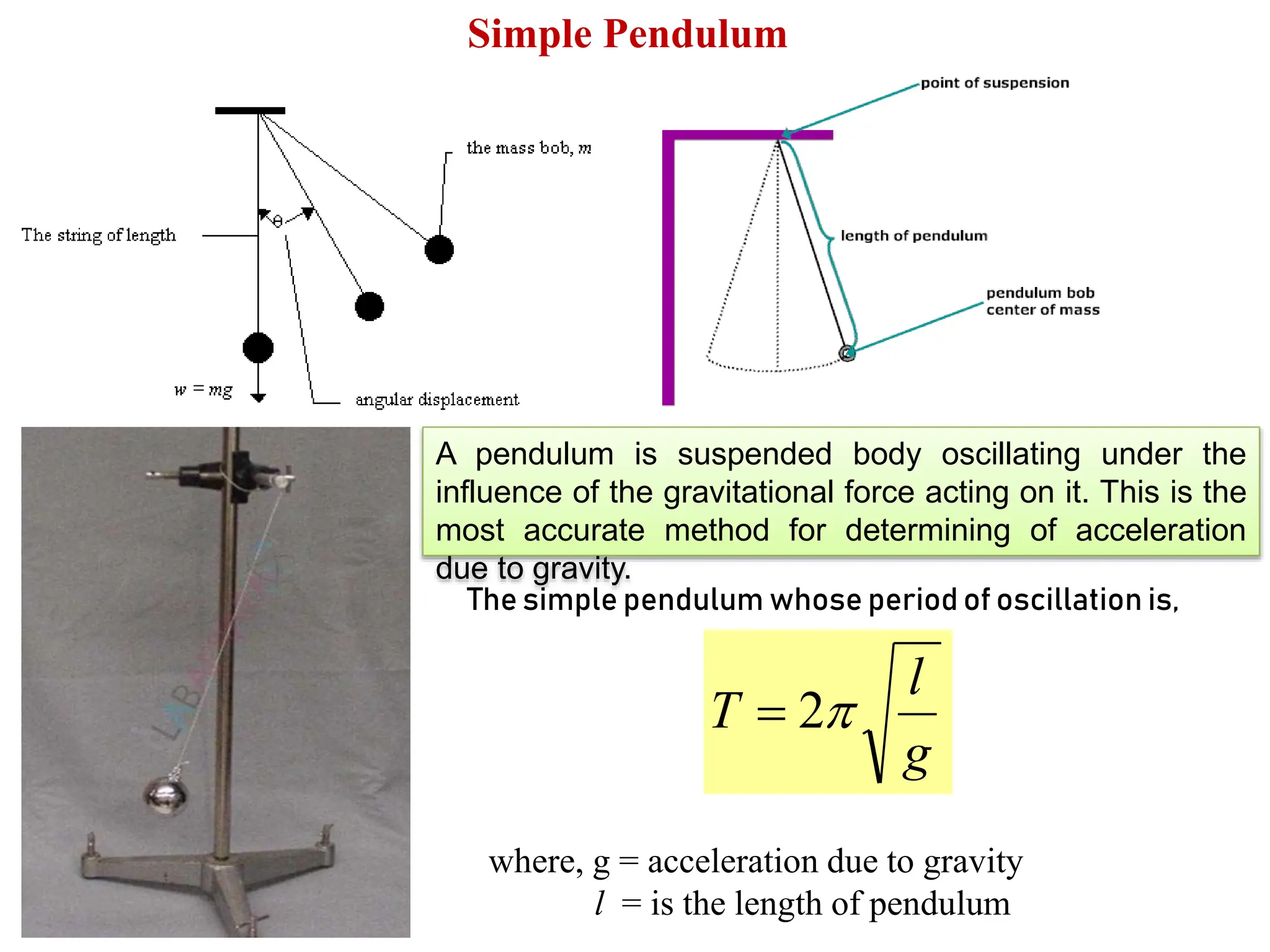
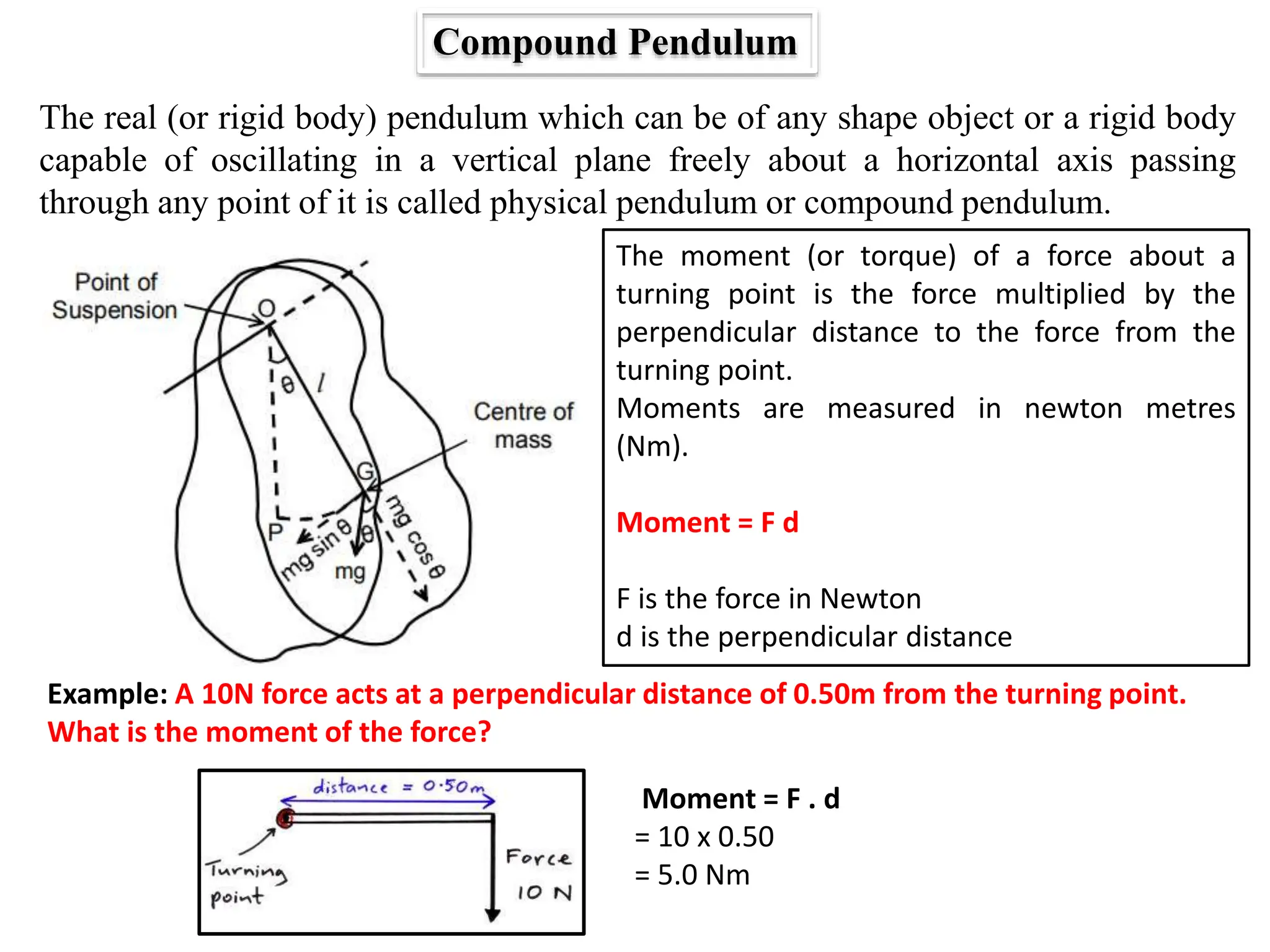
The document discusses the principles of compound and simple pendulums, detailing their time periods and the conditions influencing their oscillation. It introduces concepts such as moment of inertia, torque, and the equivalent simple pendulum length, while also explaining the significance of a reversible compound pendulum for accurately measuring gravitational acceleration. The advantages of using a compound pendulum over a simple one are highlighted, emphasizing accuracy in measurement and oscillation stability.










![In actual practice, it is extremely difficult to find the positions of the axes for the time
period T and T′ to be exactly equal.
Continued……
According to Friedrich Wilhelm Bessel, it is found that, if the two periods are nearly equal is
also sufficient.
Then the time periods of the compound pendulum of both sides (after squaring) using eqns.
(1) and (3) can be written as,
gl
l
k
T
)
(
4
2
2
2
2
------------(1)
'
)
'
(
4
2
2
2
2
gl
l
k
T
------------(3)
2
2
2
2
4
l
k
glT
2
2
2
2
'
4
'
l
k
glT
On subtracting, above equations, we get,
2
2
2
2
2
'
]
'
'
[
4
l
l
T
l
lT
g
2
2
2
2
2
'
'
'
4
l
l
T
l
lT
g
------------(6) ------------(7)
)
'
)(
'
(
'
'
4 2
2
2
l
l
l
l
T
l
lT
g
------------(8)](https://image.slidesharecdn.com/compoundpendulum-240618032540-5daf1c10/75/Mechanics-Simple-and-Compound-Pendulum-14-2048.jpg)