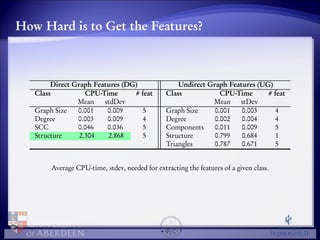
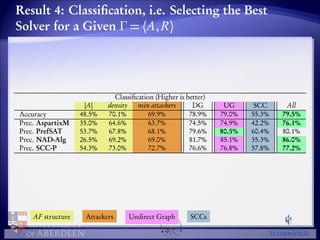
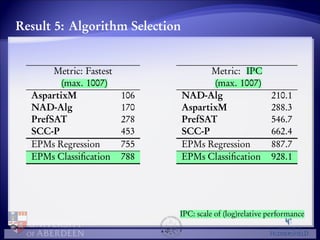
The document discusses algorithms for enumerating preferred extensions in abstract argumentation frameworks. It compares the performance of four algorithms: AspartixM, NAD-Alg, PrefSAT, and SCC-P. It finds that algorithm selection based on graph features can accurately predict runtime, with up to 80% accuracy in classification, and improves performance over a single best solver by 2-3 times. Key discriminating features include density, number of arguments, number of strongly connected components, and features related to computing graph properties.

1. Algorithm Selection for Preferred
Extensions Enumeration
Federico Cerutti, Massimiliano Giacomin, Mauro Vallati
COMMA-2014 —Wednesday 10th September, 2014

2. Background on Dung’s AF
Current Approaches for Preferred Extensions Enum.
Features
Empirical Results
Conclusions

3. Background
Definition
Given an AF = hA,Ri, with R AA:
a set S A is conflict–free if @ a,b 2 S s.t. a!b;
an argument a 2 A is acceptable with respect to a set S A if 8b 2 A s.t.
b!a, 9 c 2 S s.t. c!b;
a set S A is admissible if S is conflict–free and every element of S is
acceptable with respect to S;
a set S A is a complete extension, i.e. S 2 ECO(), iff S is admissible and
8a 2 A s.t. a is acceptable w.r.t. S, a 2 S;
a set S A is the grounded extensions, i.e. S 2 EGR(), iff S is the minimal
(w.r.t. set inclusion) complete set;
a set S A is a preferred extension, i.e. S 2 EPR(), iff S is a maximal (w.r.t. set
inclusion) complete set.

4. Background on Dung’s AF
Current Approaches for
Preferred Extensions Enum.
Features
Empirical Results
Conclusions

5. AspartixM: [Dvoˇrák et al., 2011]
Expresses argumentation semantics in Answer Set Programming
(ASP);
Tests for subset-maximality exploiting the metasp optimisation
frontend for the ASP-package gringo/claspD;
Database of the form:
farg(a) j a 2 Ag[fdefeat(a,b) j ha,bi 2 Rg
Example of program for checking the conflict–freeness:
cf = f in(X) not out(X), arg(X);
out(X) not in(X), arg(X);
in(X), in(Y), defeat(X,Y)g.

6. NAD-Alg: [Nofal et al., 2014]
Several improvements in [Nofal et al., 2014]

7. PrefSAT: [TAFA2013]
is a boolean formula such that each
satisfying assignment of the formula
corresponds to a complete extension.

8. SCC-P: [KR2014]

9. SCC-P: [KR2014]

10. SCC-P: [KR2014]

11. AspartixM // NAD-Alg // PrefSAT [DARe2014]
% Solved Average CPU-Time
Density 25% 50% 75% 25% 50% 75%
AspartixM 98.3 100.0 100.0 56.5 14.7 10.0
NAD-Alg 100.0 100.0 100.0 18.9 0.2 0.2
PrefSAT 100.0 100.0 100.0 5.1 1.6 2.2
% Solved Average CPU-Time
Density RAND RAND
AspartixM 98.9 34.0
NAD-Alg 93.9 70.6
PrefSAT 100.0 4.2

12. PrefSAT // SCC-P [KR2014]
720 AFs varying jSCC
j in 5:5:45. Size of SCCs N( = 20 : 5 : 40, = 5);
attacks among SCCs N( = 20 : 5 : 40, = 5)
100
90
80
70
60
50
40
IPC value (normalised) for SCC-P and SAT-P when 5 |SCC| 45
For jSCC
j = 35, Md(SCC-P) = 8.81,
Md(SAT-P) = 8.53, z = 0.35, p = 0.73;
0 10 20 30 40 50
|SCC|
SCC-P SAT-P

13. Background on Dung’s AF
Current Approaches for Preferred Extensions Enum.
Features
Empirical Results
Conclusions

14. Features from an Argumentation Graph = hA,Ri
— improvement from [ECAI2014]
Directed Graph (26 features)
Structure:
# vertices ( jAj )
# edges ( jRj )
# vertices / #edges ( jAj=jRj )
# edges / #vertices ( jRj=jAj )
density
average
Degree: stdev
attackers max
min
# average
stdev
max
SCCs:
min
Structure:
# self-def
# unattacked
flow hierarchy
Eulerian
aperiodic
CPU-time: . . .
Undirected Graph (24 features)
Structure:
# edges
# vertices / #edges
# edges / #vertices
density
Degree:
average
stdev
max
min
SCCs:
# average
stdev
max
min
Structure: Transitivity
3-cycles:
# average
stdev
max
min
CPU-time: . . .

15. How Hard is to Get the Features?
Direct Graph Features (DG) Undirect Graph Features (UG)
Class CPU-Time # feat Class CPU-Time # feat
Mean stdDev Mean stDev
Graph Size 0.001 0.009 5 Graph Size 0.001 0.003 4
Degree 0.003 0.009 4 Degree 0.002 0.004 4
SCC 0.046 0.036 5 Components 0.011 0.009 5
Structure 2.304 2.868 5 Structure 0.799 0.684 1
Triangles 0.787 0.671 5
Average CPU-time, stdev, needed for extracting the features of a given class.

16. Background on Dung’s AF
Current Approaches for Preferred Extensions Enum.
Features
Empirical Results
Conclusions

17. Protocol: Some Numbers
jSCC
j in 1 : 100;
jAj in 10 : 5, 000;
jRj in 25 : 270, 000 (Erdös-Rényi, p uniformly distributed) ;
Overall 10, 000 AFs.
Cutoff time of 900 seconds (value also for crashed, timed-out or ran
out of memory).
EPMs both for Regression (Random forests) and
Classification (M5-Rules) using WEKA;
Evaluation using a 10-fold cross-validation approach on a uniform
random permutation of instances.

18. Result 1: Best Features for Prediction
Solver B1 B2 B3
AspartixM number of arguments density of directed graph size of max. SCC
PrefSAT density of directed graph number of SCCs aperiodicity
NAD-Alg density of directed graph CPU-time for density CPU-time for Eulerian
SCC-P density of directed graph number of SCCs size of the max SCC
Determined by a greedy forward search based on the Correlation-based Feature Selection (CFS)
attribute evaluator.
AF structure SCCs CPU-time for feature extraction

19. Result 2: Predicting (log)Runtime
RSME of Regression (Lower is better)
B1 B2 B3 DG UG SCC All
AspartixM 0.66 0.49 0.49 0.48 0.49 0.52 0.48
PrefSAT 1.39 0.93 0.93 0.89 0.92 0.94 0.89
NAD-Alg 1.48 1.47 1.47 0.77 0.57 1.61 0.55
SCC-P 1.36 0.80 0.78 0.75 0.75 0.79 0.74
sPni
=1
log10( bti )log10( yi )
2
n
AF structure SCCs CPU-time for feature extraction Undirect Graph

20. Result 3: Best Features for Classification
C-B1 C-B2 C-B3
number of arguments density of directed graph min attackers
Determined by a greedy forward search based on the Correlation-based Feature Selection
(CFS) attribute evaluator.
AF structure Attackers

21. Result 4: Classification, i.e. Selecting the Best
Solver for a Given = hA,Ri
Classification (Higher is better)
jAj density min attackers DG UG SCC All
Accuracy 48.5% 70.1% 69.9% 78.9% 79.0% 55.3% 79.5%
Prec. AspartixM 35.0% 64.6% 63.7% 74.5% 74.9% 42.2% 76.1%
Prec. PrefSAT 53.7% 67.8% 68.1% 79.6% 80.5% 60.4% 80.1%
Prec. NAD-Alg 26.5% 69.2% 69.0% 81.7% 85.1% 35.3% 86.0%
Prec. SCC-P 54.3% 73.0% 72.7% 76.6% 76.8% 57.8% 77.2%
AF structure Attackers Undirect Graph SCCs

22. Result 5: Algorithm Selection
Metric: Fastest
(max. 1007)
AspartixM 106
NAD-Alg 170
PrefSAT 278
SCC-P 453
EPMs Regression 755
EPMs Classification 788
Metric: IPC
(max. 1007)
NAD-Alg 210.1
AspartixM 288.3
PrefSAT 546.7
SCC-P 662.4
EPMs Regression 887.7
EPMs Classification 928.1
IPC: scale of (log)relative performance

23. Background on Dung’s AF
Current Approaches for Preferred Extensions Enum.
Features
Empirical Results
Conclusions

24. Conclusions
50 features
Best algorithm selection accuracy: 80%
Algorithm selection performance: 2 times better than the best
single-solver; 3 times better than the second-best single-solver;
Consistency with previous explorations: density is among the most
informative features.
Undirect Graph Features:
AspartixM, often around [800 . . . 899] seconds — predictable?;
NAD-Alg, often time-out — predictable?;
PrefSAT, SAT-solver performance?;
SCC-P, little difference, significant?.

25. Future Work
Exploiting additional useful features;
Relevant semantics-dependent features (comparison with other
semantics);
Combining algorithms in portfolios;
Scheduling;
Ordering;
Solver combination;
Addressing problems other than enumeration (e.g. non-emptiness. . . ).

26. Acknowledgements
The authors would like to acknowledge the use of the University
of Huddersfield Queensgate Grid in carrying out this work.

27. References I
[Dvoˇrák et al., 2011] Dvoˇrák,W., Gaggl, S. A.,Wallner, J., andWoltran, S. (2011).
Making Use of Advances in Answer-Set Programming for Abstract Argumentation Systems.
In Proceedings of the 19th International Conference on Applications of Declarative Programming and Knowledge Management (INAP
2011).
[Nofal et al., 2014] Nofal, S., Atkinson, K., and Dunne, P. E. (2014).
Algorithms for decision problems in argument systems under preferred semantics.
Artificial Intelligence, 207:23–51.