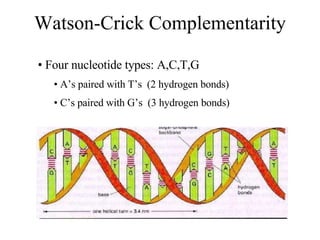
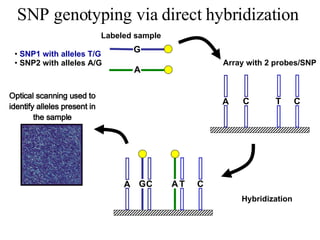
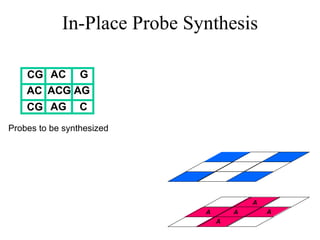
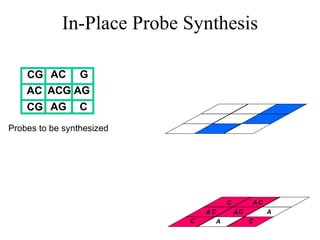
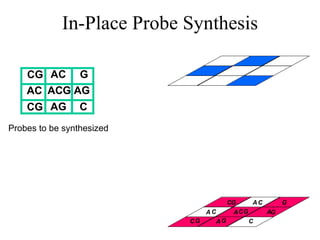
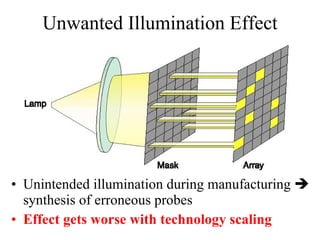
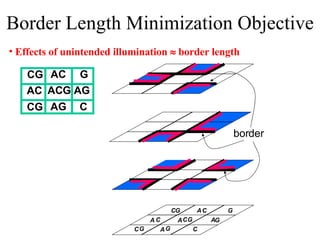
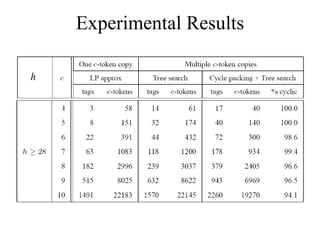
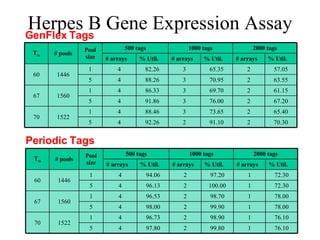
The document summarizes algorithms and techniques for biochip design and optimization. It discusses physical design of DNA arrays, tag set design for universal tag arrays, and algorithms to optimize concurrent testing on digital microfluidic biochips. Key applications include gene expression analysis, SNP genotyping, and point-of-care medical diagnosis. Design challenges involve minimizing border length in DNA arrays, maximizing tag set size while avoiding unwanted hybridization, and routing droplets on biochips to test for defects in minimal time without merging or interference.

1. Algorithms for Biochip Design and Optimization Ion Mandoiu Computer Science & Engineering Department University of Connecticut

2. Overview Physical design of DNA arrays DNA tag set design Digital microfluidic biochip testing Conclusions

3. Driver Biochip Applications Driver applications Gene expression (transcription analysis) SNP genotyping CNP analysis Genomic-based microorganism identification Point-of-care diagnosis healthcare, forensics, environmental monitoring,… As focus shifts from basic research to clinical applications, there are increasingly stringent design requirements on sensitivity, specificity, cost Assay design and optimization become critical

4. Human Genome  3  10 9 base pairs Main form of variation between individual genomes: single nucleotide polymorphisms (SNPs) Total #SNPs  1  10 7 Difference b/w any two individuals  3  10 6 SNPs (  0.1% of entire genome) Single Nucleotide Polymorphisms … ataggtcc C tatttcgcgc C gtatacacggg T ctata … … ataggtcc G tatttcgcgc A gtatacacggg A ctata … … ataggtcc C tatttcgcgc C gtatacacggg T ctata …

5. Watson-Crick Complementarity Four nucleotide types: A,C,T,G A’s paired with T’s (2 hydrogen bonds) C’s paired with G’s (3 hydrogen bonds)

6. SNP genotyping via direct hybridization Hybridization SNP1 with alleles T/G SNP2 with alleles A/G Array with 2 probes/SNP Labeled sample A C T C G A A C T C G A Optical scanning used to identify alleles present in the sample

7. In-Place Probe Synthesis CG AC CG AC ACG AG G AG C Probes to be synthesized A A A A A

8. In-Place Probe Synthesis CG AC CG AC ACG AG G AG C Probes to be synthesized A A A A A C C C C C C

9. In-Place Probe Synthesis CG AC CG AC ACG AG G AG C Probes to be synthesized A A A A A C C C C C C G G G G G G

10. Simplified DNA Array Flow Probe Selection Array Manufacturing Hybridization Experiment Gene expression levels, SNP genotypes,… Analysis of Hybridization Intensities Mask Manufacturing Physical Design: Probe Placement & Embedding Design Manufacturing End User

11. Unwanted Illumination Effect Unintended illumination during manufacturing  synthesis of erroneous probes Effect gets worse with technology scaling

12. Border Length Minimization Objective Effects of unintended illumination  border length A A A A A C C C C C C G G G G G G border CG AC CG AC ACG AG G AG C

13. Synchronous Synthesis Periodic deposition sequence, e.g., (ACTG) k Each probe grown by one nucleotide in each period  # border conflicts b/w adjacent probes = 2 x Hamming distance T G C A T G T G C A … C A period C T A C G T

14. 2D Placement Problem Find minimum cost mapping of the Hamming graph onto the grid graph Special case of the Quadratic Assignment Problem Edge cost = 2 x Hamming distance probe

15. 2D Placement: Sliding-Window Matching Slide window over entire chip Repeat fixed # of iterations (  O(N) time for fixed window size), or until improvement drops below certain threshold Proposed by [Doll et al. ‘94] in VLSI context 1 3 2 5 4 Select mutually nonadjacent probes from small window 2 2 3 1 4 Re-assign optimally

16. 2D Placement: Epitaxial Growth Proposed by [PreasL’88, ShahookarM’91] in VLSI context Simulates crystal growth Efficient “row” implementation Use lexicographical sorting for initial ordering of probes Fill cells row-by-row Bound number of candidate probes considered when filling each cell Constant # of lookahead rows  O(N 3/2 ) runtime, N = #probes

17. 2D Placement: Recursive Partitioning Very effective in VLSI placement [AlpertK’95,Caldwell et al.’00] 4-way partition using linear time clustering Repeat until Row-Epitaxial can be applied

18. Asynchronous Synthesis A A A C C C T T T G G G A C T G A G T G T G A A Deposition Sequence Probes Synchronous Embedding A G T A G G T A G A A G T A G T ASAP Embedding G

19. Efficient solution by dynamic programming Optimal Single-Probe Re-Embedding A C T A C G T A C G T Source Sink

20. In-Place Re-Embedding Algorithms 2D placement fixed, allow only probe embeddings to change Greedy: optimally re-embed probe with largest gain Chessboard: alternate re-embedding of black/white cells Sequential: re-embed probes row-by-row CPU %LB CPU %LB CPU %LB 121.4 120.5 Chessboard 1423 54 127.1 125.7 Greedy 120.9 119.9 Sequential 1535 943 500 64 40 100 Chip size

21. Integration with Probe Selection Probe Selection Physical Design: Placement & Embedding Probe Pools Chip size 100x100 Pool Row-Epitaxial Pool Size 7515 15.2 16 3645 11.8 8 1796 8.2 4 1040 4.3 2 217 - 1 CPU sec. % Improv

22. Overview Physical design of DNA arrays DNA tag set design Digital microfluidic biochip testing Conclusions

23. Universal Tag Arrays Brenner 97, Morris et al. 98 Array consisting of application independent tags Two-part “reporter” probes: aplication specific primers ligated to antitags Detection carried by a sequence of reactions separately involving the primer and the antitag part of reporter probes

24. Universal Tag Array Advantages Cost effective Same tag array used for different analyses  can be mass-produced Only need to synthesize new set of reporter probes More reliable! Solution phase hybridization better understood than hybridization on solid support

25. SNP Genotyping with Tag Arrays Tag + Primer G A G C antitag Mix reporter probes with unlabeled genomic DNA 2. Solution phase hybridization 3. Single-Base Extension (SBE) 4. Solid phase hybridization G A G G A G T G A T C C T C C

26. Tag Set Design Problem (H1) Tags hybridize strongly to complementary antitags (H2) No tag hybridizes to a non-complementary antitag t1 t1 t2 t2 t1 t2 t1 Tag Set Design Problem: Find a maximum cardinality set of tags satisfying (H1)-(H2)

27. Hybridization Models Melting temperature Tm: temperature at which 50% of duplexes are in hybridized state 2-4 rule Tm = 2 #(As and Ts) + 4 #(Cs and Gs) More accurate models exist, e.g., the near-neighbor model

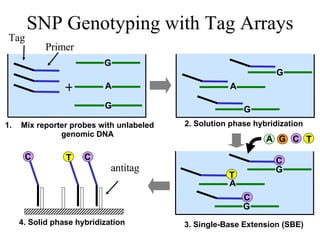
28. Hamming distance model, e.g., [Marathe et al. 01] Models rigid DNA strands LCS/edit distance model, e.g., [Torney et al. 03] Models infinitely elastic DNA strands c-token model [Ben-Dor et al. 00]: Duplex formation requires formation of nucleation complex between perfectly complementary substrings Nucleation complex must have weight  c, where wt(A)=wt(T)=1, wt(C)=wt(G)=2 (2-4 rule) Hybridization Models (contd.)

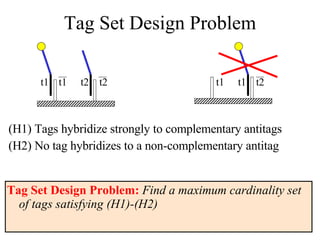
29. c-h Code Problem c-token: left-minimal DNA string of weight  c, i.e., w(x)  c w(x’) < c for every proper suffix x’ of x A set of tags is a c-h code if (C1) Every tag has weight  h (C2) Every c-token is used at most once c-h Code Problem [Ben-Dor et al.00] Given c and h, find maximum cardinality c-h code

30. Algorithms for c-h Code Problem [Ben-Dor et al.00] approximation algorithm based on DeBruijn sequences Alphabetic tree search algorithm Enumerate candidate tags in lexicographic order, save tags whose c-tokens are not used by previously selected tags Easily modified to handle various combinations of constraints [MT 05, 06] Optimum c-h codes can be computed in practical time for small values of c by using integer programming Practical runtime using Garg-Koneman approximation and LP-rounding

31. Token Content of a Tag c=4 CCAGATT CC CCA CAG AGA GAT GATT Tag  sequence of c-tokens End pos: 2 3 4 5 6 7 c-token: CC  CCA  CAG  AGA  GAT  GATT

32. Layered c-token graph for length-l tags s t c 1 c N l l-1 c/2 (c/2)+1 …

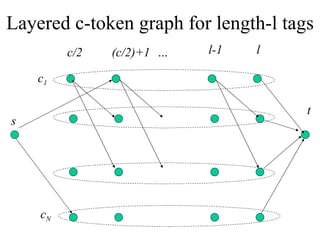
33. Integer Program Formulation [MPT05] Maximum integer flow problem w/ set capacity constraints O( hN) constraints & variables, where N = #c-tokens

34. Packing LP Formulation

35. Garg-Konemann Algorithm x  0; y   // y i are variables of the dual LP Find min weight s-t path p, where weight(v) = y i for every v  V i While weight(p) < 1 do M  max i |p  V i | x p  x p + 1/M For every i, y i  y i ( 1 +  * |p  V i |/M ) Find min weight s-t path p, where weight(v) = y i for v  V i 4. For every p, x p  x p / (1 - log 1+   ) [GK98] The algorithm computes a factor (1-  ) 2 approximation to the optimal LP solution with (N/  )* log 1+  N shortest path computations

36. LP Based Tag Set Design Run Garg-Konemann and store the minimum weight paths in a list Traversing the list in reverse order, pick tags corresponding to paths if they are feasible and do not share c-tokens with already selected tags Mark used c-tokens and run the alphabetic tree search algorithm to select additional tags

37. Periodic Tags [MT05] Key observation: c-token uniqueness constraint in c-h code formulation is too strong A c-token should not appear in two different tags, but can be repeated in a tag A tag t is called periodic if it is the prefix of (  )  for some “period”  Periodic strings make best use of c-tokens

38. c-token factor graph, c=4 (incomplete) CC AAG AAC AAAA AAAT

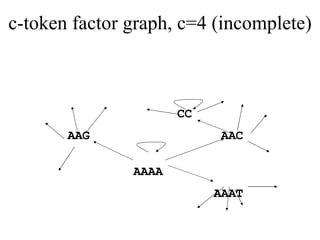
39. Vertex-disjoint Cycle Packing Problem Given directed graph G, find maximum number of vertex disjoint directed cycles in G [MT 05] APX-hard even for regular directed graphs with in-degree and out-degree 2 h-c/2+1 approximation factor for tag set design problem [Salavatipour and Verstraete 05] Quasi-NP-hard to approximate within  (log 1-  n) O(n 1/2 ) approximation algorithm

40. Cycle Packing Algorithm Construct c-token factor graph G T  {} For all cycles C defining periodic tags, in increasing order of cycle length, Add to T the tag defined by C Remove C from G Perform an alphabetic tree search and add to T tags consisting of unused c-tokens Return T

41. Experimental Results h

42. More Hybridization Constraints… Enforced during tag assignment by - Leaving some tags unassigned and distributing primers across multiple arrays [Ben-Dor et al. 03] - Exploiting availability of multiple primer candidates [MPT05] t1 t2 t1

43. Herpes B Gene Expression Assay GenFlex Tags Periodic Tags % Util. # arrays % Util. # arrays % Util. # arrays 76.10 1 99.80 2 97.80 4 5 76.10 1 98.90 2 96.73 4 1 1522 70 78.00 1 99.90 2 98.00 4 5 78.00 1 98.70 2 96.53 4 1 1560 67 72.30 1 100.00 2 96.13 4 5 72.30 1 97.20 2 94.06 4 1 1446 60 2000 tags 1000 tags 500 tags Pool size # pools T m % Util. # arrays % Util. # arrays % Util. # arrays 70.30 2 91.10 2 92.26 4 5 65.40 2 73.65 3 88.46 4 1 1522 70 67.20 2 76.00 3 91.86 4 5 61.15 2 69.70 3 86.33 4 1 1560 67 63.55 2 70.95 3 88.26 4 5 57.05 2 65.35 3 82.26 4 1 1446 60 2000 tags 1000 tags 500 tags Pool size # pools T m

44. Overview Physical design of DNA arrays DNA tag set design Digital microfluidic biochip testing Conclusions

45. Digital Microfluidic Biochips [Srinivasan et al. 04] Electrodes typically arranged in rectangular grid Droplets moved by applying voltage to adjacent cell Can be used for analyses of DNA, proteins, metabolites… [Su&Chakrabarty 06] I/O I/O Cell

46. Design Challenges Testing High electrode failure rate, but can re-configure around Performed both after manufacturing and concurrent with chip operation Main objective is minimization of completion time Module placement Assay operations (mixing, amplification, etc.) can be mapped to overlapping areas of the chip if performed at different times Droplet routing When multiple droplets are routed simultaneously must prevent accidental droplet merging or interference Merging Interference

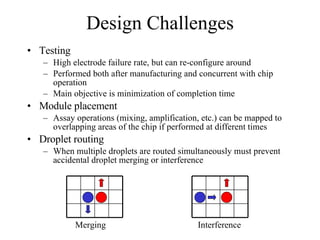
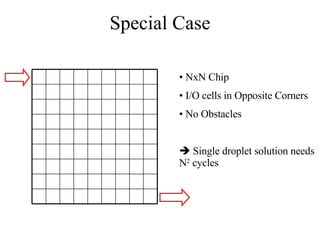
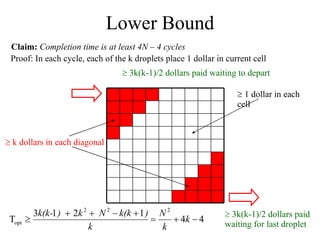
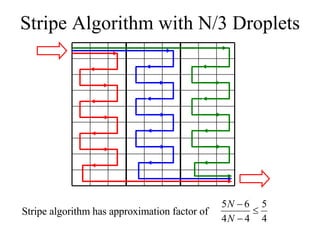
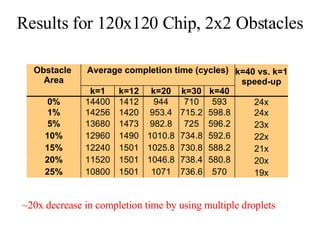
47. Concurrent Testing Problem GIVEN: Input/Output cells Position of obstacles (cells in use by ongoing reactions) FIND: Trajectories for test droplets such that Every non-blocked cell is visited by at least one test droplet Droplet trajectories meet non-merging and non-interference constraints Completion time is minimized Defect model: test droplet gets stuck at defective electrode [Su et al. 04] ILP-based solution for single test droplet case & heuristic for multiple input-output pairs with single test droplet/pair

48. ILP Formulation for Unconstrained Number of Droplets Each cell (i,j) visited at least once: Droplet conservation: No droplet merging: No droplet interference: Minimize completion time:

49. Special Case NxN Chip I/O cells in Opposite Corners No Obstacles  Single droplet solution needs N 2 cycles

50. Lower Bound Claim: Completion time is at least 4N – 4 cycles Proof: In each cycle, each of the k droplets place 1 dollar in current cell  3k(k-1)/2 dollars paid waiting to depart  3k(k-1)/2 dollars paid waiting for last droplet  k dollars in each diagonal  1 dollar in each cell

51. Stripe Algorithm with N/3 Droplets Stripe algorithm has approximation factor of

52. Stripe Algorithm with Obstacles of width Q Divide array into vertical stripes of width Q+1 Use one droplet per stripe All droplets visit cells in assigned stripes in parallel In case of interference droplet on left stripe waits for droplet in right stripe

53. Results for 120x120 Chip, 2x2 Obstacles ~20x decrease in completion time by using multiple droplets 19x 570 736.6 1071 1501 10800 25% 20x 580.8 738.4 1046.8 1501 11520 20% 21x 588.2 730.8 1025.8 1501 12240 15% 22x 592.6 734.8 1010.8 1490 12960 10% 23x 596.2 725 982.8 1473 13680 5% 24x 598.8 715.2 953.4 1420 14256 1% 24x 593 710 944 1412 14400 0% k=40 k=30 k=20 k=12 k=1 k=40 vs. k=1 speed-up Average completion time (cycles) Obstacle Area

54. Overview Physical design of DNA arrays DNA tag set design Digital microfluidic biochip testing Conclusions

55. Conclusions Biochip design is a fertile area of applications Combinatorial optimization techniques can yield significant improvements in assay quality/throughput Very dynamic area, driver applications and underlying technologies change rapidly

56. Acknowledgments Physical design of DNA arrays: A.B. Kahng, P. Pevzner, S. Reda, X. Xu, A. Zelikovsky Tag set design: D. Trinca Testing of digital microfluidic biochips: R. Garfinkel, B. Pasaniuc, A. Zelikovsky Financial support: UCONN Research Foundation, NSF awards 0546457 and 0543365

57. Questions?